Affine Hecke algebra plays a crucial role in representation theory and harmonic analysis, offering a rich structure that connects algebraic groups and quantum groups. Its applications span various areas, including number theory, algebraic geometry, and mathematical physics, providing powerful tools to understand symmetry and invariant theory. Explore the article to deepen your understanding of affine Hecke algebras and their significance in modern mathematics.
Table of Comparison
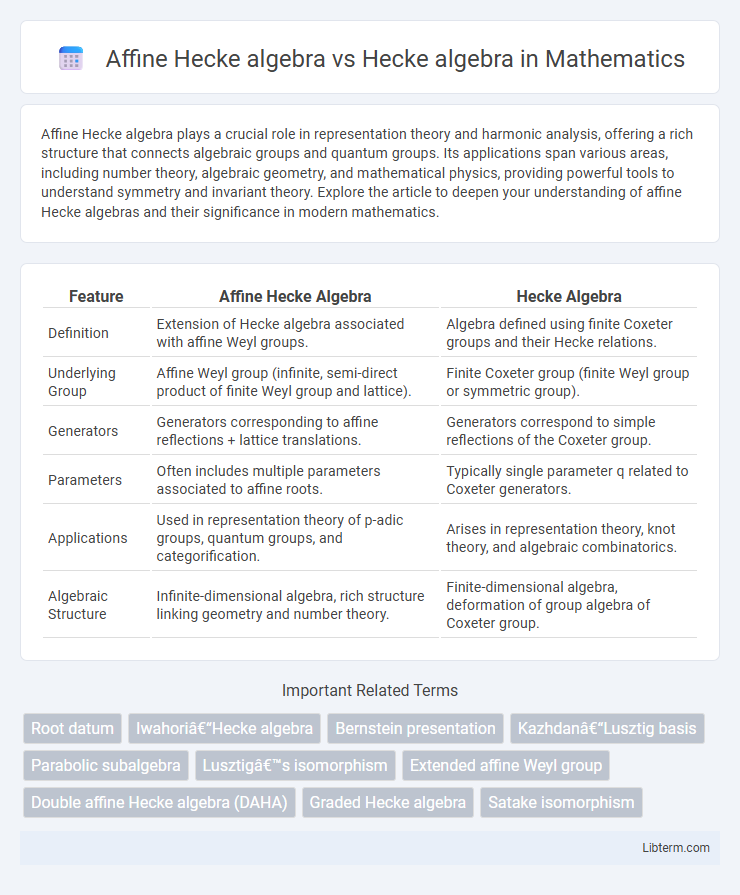
| Feature | Affine Hecke Algebra | Hecke Algebra |
|---|---|---|
| Definition | Extension of Hecke algebra associated with affine Weyl groups. | Algebra defined using finite Coxeter groups and their Hecke relations. |
| Underlying Group | Affine Weyl group (infinite, semi-direct product of finite Weyl group and lattice). | Finite Coxeter group (finite Weyl group or symmetric group). |
| Generators | Generators corresponding to affine reflections + lattice translations. | Generators correspond to simple reflections of the Coxeter group. |
| Parameters | Often includes multiple parameters associated to affine roots. | Typically single parameter q related to Coxeter generators. |
| Applications | Used in representation theory of p-adic groups, quantum groups, and categorification. | Arises in representation theory, knot theory, and algebraic combinatorics. |
| Algebraic Structure | Infinite-dimensional algebra, rich structure linking geometry and number theory. | Finite-dimensional algebra, deformation of group algebra of Coxeter group. |
Introduction to Hecke Algebras
Hecke algebras are algebraic structures arising from group theory, particularly associated with Coxeter groups, and play a crucial role in representation theory and number theory. Affine Hecke algebras extend classical Hecke algebras by incorporating affine Weyl groups, allowing a richer structure that encodes translation symmetries alongside reflections. These algebras facilitate deeper analysis of p-adic groups and connections to quantum groups, making them fundamental in modern algebraic and geometric representation theory.
Understanding Affine Hecke Algebras
Affine Hecke algebras are extensions of Hecke algebras associated with affine Weyl groups, incorporating both finite Weyl group symmetries and translations from the affine lattice, which enrich their algebraic structure. These algebras play a crucial role in representation theory and harmonic analysis, particularly in the study of p-adic groups and double affine Hecke algebras (DAHA). Understanding affine Hecke algebras involves analyzing their generators, relations, and parameter dependencies, which distinguishes them from finite Hecke algebras and enables applications in categorification and geometric representation theory.
Historical Background and Motivation
The Affine Hecke algebra arose in the 1970s as an extension of the classical Hecke algebra to better understand representations of p-adic groups and their harmonic analysis, with significant contributions by Iwahori and Matsumoto. While the Hecke algebra originated from the study of finite Coxeter groups and modular forms, the Affine Hecke algebra incorporates affine Weyl groups, providing a richer algebraic structure capturing infinite-dimensional phenomena. This development was motivated by the need to generalize Hecke operators in number theory and representation theory, linking geometric and combinatorial methods in the classification of representations.
Structural Differences: Affine vs Classical Hecke Algebras
Affine Hecke algebras extend classical Hecke algebras by incorporating a deformation parameter linked to affine Weyl groups, resulting in a richer algebraic structure that combines group algebra elements with polynomial parts. The classical Hecke algebra is associated with finite Coxeter groups and relies on relations tied to finite root systems, whereas affine Hecke algebras correspond to affine root systems, introducing infinite-dimensional features and complex representation theory. Structural differences include the presence of additional generators related to translations in affine Hecke algebras, which are absent in the classical setting, significantly affecting their module categories and harmonic analysis applications.
Representation Theory: Key Distinctions
Affine Hecke algebras generalize finite Hecke algebras by incorporating affine Weyl groups, leading to richer representation theory with infinite-dimensional modules and more intricate category structures. Representations of affine Hecke algebras are closely linked to the geometric Langlands program and double affine Hecke algebras (DAHA), offering a deeper framework for harmonic analysis on p-adic groups. In contrast, finite Hecke algebras primarily yield finite-dimensional representations associated with Coxeter groups, serving as a foundational tool for studying symmetric group representations and finite reductive groups.
Generators and Relations Comparison
Affine Hecke algebras extend classical Hecke algebras by incorporating translations from the affine Weyl group, generated by simple reflections \(T_i\) and multiplicative elements \(X^\lambda\) corresponding to the weight lattice. Hecke algebras are generated solely by simple reflections \(T_i\) satisfying braid relations and quadratic relations \((T_i - q)(T_i + 1) = 0\), while affine Hecke algebras augment these with commutation relations linking \(T_i\) and \(X^\lambda\), such as \(T_i X^\lambda - X^{s_i(\lambda)} T_i = (q-1)\frac{X^\lambda - X^{s_i(\lambda)}}{1 - X^{-\alpha_i}}\). The interplay of these added generators and relations allows affine Hecke algebras to capture richer representation-theoretic phenomena and connect with double affine Hecke algebras.
Applications in Number Theory and Geometry
Affine Hecke algebras and Hecke algebras play crucial roles in number theory and geometry by providing frameworks for studying automorphic forms and representational aspects of p-adic groups. Affine Hecke algebras extend classical Hecke algebras through connections with affine Weyl groups, enabling refined analysis in the representation theory of Lie groups and applications in geometric representation theory, such as the categorification of Hecke algebra modules. These structures facilitate deep insights into Langlands program conjectures, harmonic analysis on reductive groups, and the study of Shimura varieties and modular forms.
Role in the Theory of Quantum Groups
Affine Hecke algebras generalize finite Hecke algebras by incorporating parameters related to affine Weyl groups, playing a crucial role in the representation theory of quantum groups and categorification. These algebras provide a framework for understanding module categories over quantum groups at roots of unity and facilitate the construction of canonical bases in quantum group theory. Finite Hecke algebras, by contrast, primarily encode symmetry and braid group actions, serving as tools for studying representations of finite groups of Lie type without the extended affine structure essential to quantum group dualities.
Connections to Symmetric Functions and Schur Polynomials
Affine Hecke algebras generalize classical Hecke algebras by incorporating affine Weyl groups, leading to richer representation theory and deeper connections with symmetric functions. The study of affine Hecke algebras relates directly to Macdonald polynomials, which generalize Schur polynomials and encode significant combinatorial and algebraic information. In contrast, classical Hecke algebras are closely linked to Schur polynomials through their role in the representation theory of symmetric groups and the study of symmetric functions in algebraic combinatorics.
Open Problems and Future Research Directions
Open problems in the study of affine Hecke algebras center on their representation theory's deeper connections with affine Lie algebras and p-adic groups, specifically understanding the classification of irreducible modules and character formulas. Future research directions emphasize exploring categorical and geometric interpretations via the geometric Langlands program and seeking extensions to double affine Hecke algebras (DAHAs) that could unveil new symmetry structures in algebraic combinatorics and mathematical physics. Developing computational tools for explicit module construction and establishing connections with quantum groups represent crucial ongoing challenges in the field.
Affine Hecke algebra Infographic
 libterm.com
libterm.com