The orthogonal complement of a subspace in a vector space consists of all vectors that are perpendicular to every vector in the original subspace, playing a critical role in linear algebra and functional analysis. Understanding this concept helps solve problems related to projections, decompositions, and solving systems of linear equations. Explore the rest of the article to deepen your grasp of orthogonal complements and their applications.
Table of Comparison
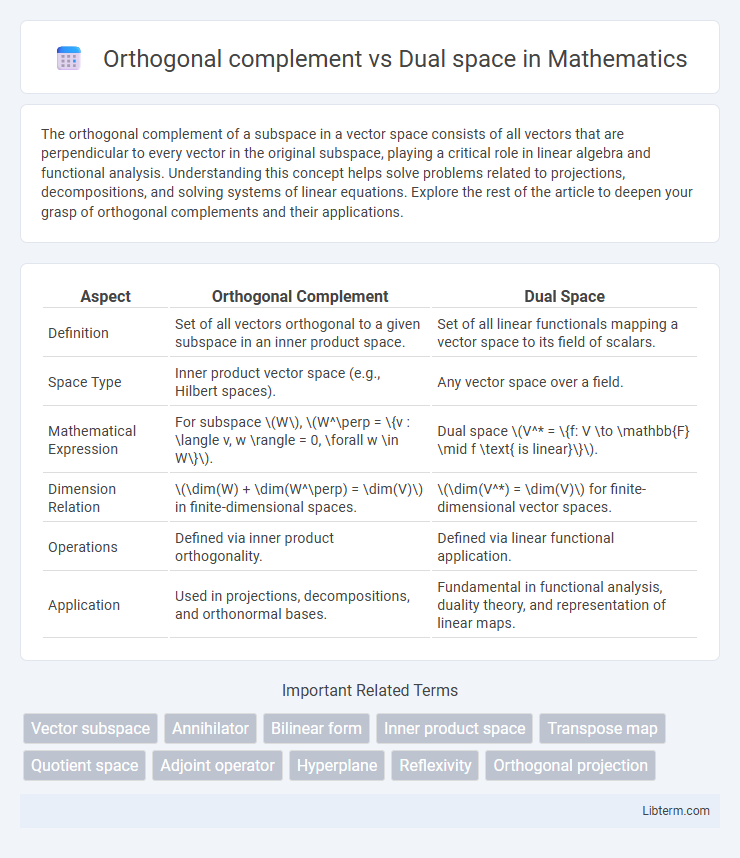
| Aspect | Orthogonal Complement | Dual Space |
|---|---|---|
| Definition | Set of all vectors orthogonal to a given subspace in an inner product space. | Set of all linear functionals mapping a vector space to its field of scalars. |
| Space Type | Inner product vector space (e.g., Hilbert spaces). | Any vector space over a field. |
| Mathematical Expression | For subspace \(W\), \(W^\perp = \{v : \langle v, w \rangle = 0, \forall w \in W\}\). | Dual space \(V^* = \{f: V \to \mathbb{F} \mid f \text{ is linear}\}\). |
| Dimension Relation | \(\dim(W) + \dim(W^\perp) = \dim(V)\) in finite-dimensional spaces. | \(\dim(V^*) = \dim(V)\) for finite-dimensional vector spaces. |
| Operations | Defined via inner product orthogonality. | Defined via linear functional application. |
| Application | Used in projections, decompositions, and orthonormal bases. | Fundamental in functional analysis, duality theory, and representation of linear maps. |
Introduction to Orthogonal Complement and Dual Space
The orthogonal complement of a subspace in an inner product space consists of all vectors that are orthogonal to every vector in that subspace, forming a fundamental concept in linear algebra and functional analysis. The dual space, defined as the set of all linear functionals mapping a vector space to its underlying field, provides a crucial framework for studying linear transformations and bilinear forms. Understanding the orthogonal complement and dual space enables deeper insights into vector space structure, projection theory, and duality principles.
Definitions: Orthogonal Complement vs. Dual Space
The orthogonal complement of a subspace in an inner product space consists of all vectors orthogonal to every vector in that subspace, defined by the inner product zero condition. The dual space of a vector space is the set of all linear functionals mapping vectors to the underlying field, capturing linear mappings rather than vector elements themselves. While the orthogonal complement relates to geometric properties within the vector space, the dual space emphasizes functional mappings, providing distinct but complementary perspectives in linear algebra.
Geometric Interpretations
The orthogonal complement of a subspace in an inner product space consists of all vectors perpendicular to every vector in the subspace, forming a geometric "shadow" that captures directions orthogonal to it. The dual space, composed of all linear functionals mapping vectors to scalars, represents a geometric plane of evaluation rather than a spatial subspace, providing a framework to measure or assign values to vectors. While the orthogonal complement visually represents perpendicular geometric directions, the dual space abstracts vector properties into scalar measurements, linking geometric intuition with functional analysis.
Algebraic Characterization
The orthogonal complement of a subspace \( W \) in a vector space \( V \) consists of all vectors in \( V \) that yield zero when paired with every vector in \( W \) under an inner product. The dual space \( V^* \) is the set of all linear functionals mapping vectors in \( V \) to the underlying field, providing an algebraic characterization as a space of linear maps rather than vectors. The orthogonal complement can be identified with the kernel of the evaluation map induced by elements of \( V^* \), establishing a fundamental link between inner product structures and dual space functionals for subspace analysis.
Relationship and Differences
The orthogonal complement of a subspace in an inner product space consists of all vectors orthogonal to every vector in that subspace, whereas the dual space comprises all linear functionals mapping vectors to the underlying field. The relationship between them is realized through the Riesz representation theorem, which establishes an isometric isomorphism between a Hilbert space and its dual, linking orthogonal complements to kernels of functionals in the dual space. Differences arise because orthogonal complements depend on the inner product structure and are subspaces within the original space, while dual spaces are vector spaces of linear maps defined independently of any inner product.
Applications in Linear Algebra
The orthogonal complement in linear algebra identifies all vectors perpendicular to a given subspace, crucial in solving linear systems and projecting vectors. The dual space consists of all linear functionals mapping vectors to scalars, facilitating the study of matrix transposes and defining adjoint operators. Applications in optimization, such as characterizing null spaces and range spaces, leverage both concepts to analyze vector spaces and linear transformations efficiently.
Role in Inner Product Spaces
The orthogonal complement in an inner product space consists of all vectors orthogonal to a given subspace, serving as a geometric tool to decompose vectors and analyze projections. The dual space, formed by all continuous linear functionals, provides an algebraic framework to study inner product spaces through linear mappings. The Riesz representation theorem connects these concepts by establishing an isometric isomorphism between an inner product space and its dual, emphasizing their complementary roles in functional analysis.
Examples in Finite-Dimensional Spaces
Orthogonal complements in finite-dimensional inner product spaces consist of all vectors orthogonal to a given subspace, such as the orthogonal complement of a plane in \(\mathbb{R}^3\), which is a line, while dual spaces comprise all linear functionals mapping vectors to scalars, exemplified by the dual space of \(\mathbb{R}^n\) being the set of all linear maps from \(\mathbb{R}^n\) to \(\mathbb{R}\). In \(\mathbb{R}^2\) with the standard dot product, the orthogonal complement of a vector \(\mathbf{v}\) is the line perpendicular to \(\mathbf{v}\), whereas its dual space consists of all linear functions such as \(f(x,y) = ax + by\). The dimension of the orthogonal complement plus the dimension of the original subspace equals the dimension of the vector space, and the dual space shares the same dimension as the original space, illustrating key structural differences.
Connections to Functional Analysis
The orthogonal complement of a subspace in a Hilbert space captures all vectors orthogonal to that subspace, playing a crucial role in projection theory and spectral analysis. The dual space consists of all continuous linear functionals on a vector space, forming the foundation for defining weak topologies and analyzing operator adjoints. Both concepts intertwine through the Riesz representation theorem, which identifies the dual space of a Hilbert space with itself via inner products, linking orthogonal complements to the characterization of functionals in functional analysis.
Summary and Key Takeaways
The orthogonal complement of a subspace in an inner product space consists of all vectors orthogonal to that subspace, highlighting geometric intuition and perpendicularity concepts. The dual space comprises all linear functionals mapping vectors to their underlying field, emphasizing functional analysis and linear mappings. Key takeaways include understanding that the orthogonal complement relates to inner products and geometry, while the dual space generalizes function evaluation in linear algebra, both essential in advanced vector space theory.
Orthogonal complement Infographic
 libterm.com
libterm.com