A polyhedron is a three-dimensional solid figure composed of flat polygonal faces, straight edges, and sharp vertices, often studied in geometry and architecture for its structural properties. Understanding the classification of polyhedra, such as regular, irregular, convex, and concave types, can enhance your spatial reasoning and design skills. Explore the full article to discover the fascinating world of polyhedra and their applications.
Table of Comparison
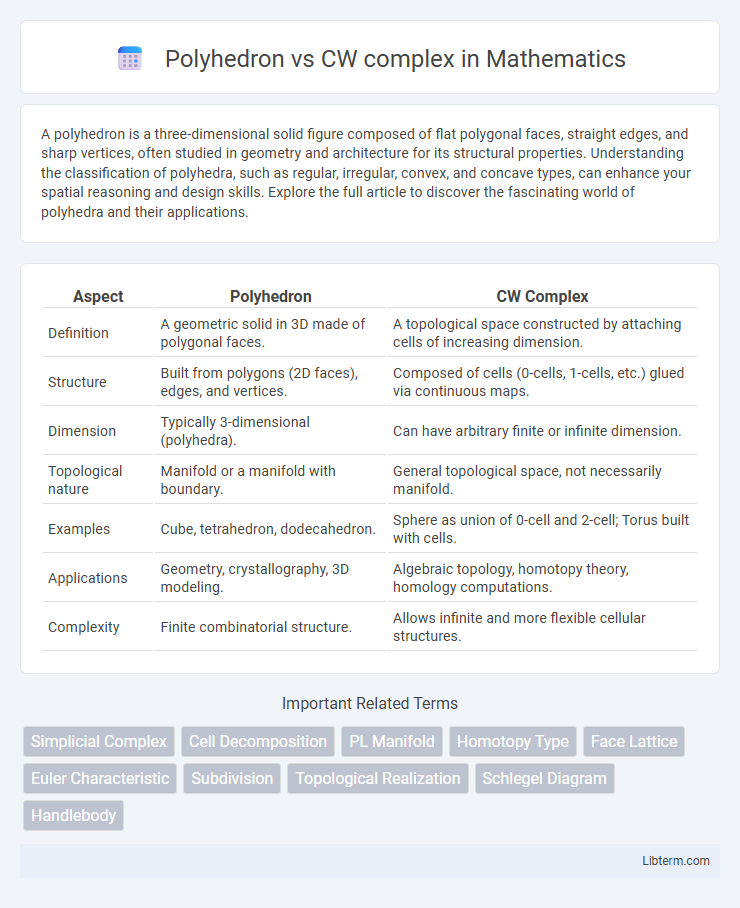
| Aspect | Polyhedron | CW Complex |
|---|---|---|
| Definition | A geometric solid in 3D made of polygonal faces. | A topological space constructed by attaching cells of increasing dimension. |
| Structure | Built from polygons (2D faces), edges, and vertices. | Composed of cells (0-cells, 1-cells, etc.) glued via continuous maps. |
| Dimension | Typically 3-dimensional (polyhedra). | Can have arbitrary finite or infinite dimension. |
| Topological nature | Manifold or a manifold with boundary. | General topological space, not necessarily manifold. |
| Examples | Cube, tetrahedron, dodecahedron. | Sphere as union of 0-cell and 2-cell; Torus built with cells. |
| Applications | Geometry, crystallography, 3D modeling. | Algebraic topology, homotopy theory, homology computations. |
| Complexity | Finite combinatorial structure. | Allows infinite and more flexible cellular structures. |
Introduction to Polyhedra and CW Complexes
Polyhedra are geometric objects formed by joining polygons along their edges to create a solid figure, often studied in topology and combinatorics. CW complexes provide a more flexible framework by assembling spaces from cells of various dimensions, connected via continuous maps, enabling complex topological constructions beyond polyhedral shapes. Understanding the differences between polyhedra and CW complexes is essential for exploring advanced geometric and topological properties in mathematical research.
Defining Polyhedra: Key Properties
Polyhedra are defined as geometric solids in three dimensions bounded by flat polygonal faces, straight edges, and sharp vertices, each face being a convex polygon. Key properties include being a finite union of polygons that meet only along shared edges or vertices, ensuring a well-defined boundary and interior. Unlike CW complexes, polyhedra possess a rigid geometric structure characterized by flat faces and linear edges, making them a foundational concept in classical geometry and combinatorial topology.
Understanding the CW Complex Structure
CW complexes provide a flexible framework for building topological spaces by inductively attaching cells of increasing dimension via characteristic maps, allowing for a clear combinatorial and algebraic structure that is often more general than polyhedra. Unlike polyhedra, which are formed by gluing simplices along faces to create a piecewise-linear space, CW complexes may include cells that are not simplices and afford greater versatility in homotopy theory and algebraic topology. Understanding the CW complex structure involves analyzing its cellular decomposition, the attaching maps defining the topology, and properties like closure-finiteness and the weak topology condition, facilitating computations of homotopy and homology groups beyond polyhedral constraints.
Historical Context: Polyhedra vs CW Complex Origins
Polyhedra trace back to ancient Greek mathematics, where Plato and Euclid studied their geometric and spatial properties, forming the foundation of classical geometry. CW complexes emerged in the 20th century through algebraic topology, introduced by J.H.C. Whitehead to generalize cell complexes and facilitate homotopy theory analysis. The shift from polyhedra to CW complexes marks a transition from combinatorial geometry to more abstract and flexible topological structures.
Topological Differences Between Polyhedra and CW Complexes
Polyhedra are formed by gluing together simplices along their faces, resulting in a combinatorial and geometric structure with a fixed embedding in Euclidean space, whereas CW complexes are constructed by attaching cells via continuous maps, allowing for more flexible topological configurations. The topological differences arise because CW complexes can represent spaces with complicated identifications and non-simplicial attachments, often yielding homotopy equivalences that are not realizable by polyhedra alone. Unlike polyhedra, CW complexes are useful for modeling a broader class of topological spaces due to their inductive cell-by-cell construction and minimal geometric constraints.
Examples of Polyhedra in Geometry
Polyhedra in geometry include classic examples such as the Platonic solids--tetrahedron, cube, octahedron, dodecahedron, and icosahedron--each characterized by regular polygonal faces and identical vertices. Unlike CW complexes, which are built by gluing cells of varying dimensions in a topological space, polyhedra possess a finite arrangement of polygonal faces meeting along edges and vertices, providing concrete combinatorial structures. Other geometric polyhedra examples include Archimedean solids and Johnson solids, which expand the classification with semi-regular and convex forms, respectively.
Illustrative CW Complex Constructions
CW complexes provide a flexible framework for constructing topological spaces by successively attaching cells via continuous maps, offering a more general approach than polyhedra, which are built from simplices glued along faces. Illustrative CW complex constructions often involve building spaces such as spheres, tori, and projective planes through explicit attaching maps of n-cells, highlighting the cellular structure beyond the combinatorial constraints of polyhedra. The adaptability in defining cells and their attaching maps allows CW complexes to represent a wider class of spaces with well-understood homotopy and homology theories, contrasting with the more rigid, combinatorial nature of polyhedral constructions.
Applications of Polyhedra and CW Complexes
Polyhedra serve as fundamental structures in computational geometry, computer graphics, and optimization problems, where their well-defined vertices, edges, and faces enable efficient algorithms for mesh generation and 3D modeling. CW complexes find extensive application in algebraic topology and homotopy theory, providing a flexible framework for decomposing spaces into cells to study their topological properties and compute invariants such as homology and cohomology groups. Both polyhedra and CW complexes facilitate the analysis of spatial structures, but CW complexes are particularly powerful in higher-dimensional topology and abstract homotopical constructions.
Advantages and Limitations: Polyhedron vs CW Complex
Polyhedra offer a rigid geometric structure ideal for finite computational models and explicit triangulations, facilitating straightforward combinatorial manipulations and visualizations. CW complexes provide greater flexibility in topological constructions, enabling the attachment of cells of varying dimensions and accommodating infinite or more abstract spaces beyond polyhedral shapes. Polyhedral limitations include difficulty representing spaces with complicated topology, whereas CW complexes may lack explicit geometric realizations, complicating metric analyses and numerical applications.
Conclusion: Choosing Between Polyhedron and CW Complex
Choosing between a polyhedron and a CW complex depends on the specific application and desired level of topological flexibility; polyhedra offer a concrete, combinatorial structure ideal for computational geometry and visualization, while CW complexes provide a more general, algebraic framework suited for advanced homotopy and homology computations. Polyhedra consist of simplicial complexes with well-defined geometric embeddings, facilitating explicit constructions, whereas CW complexes allow cell attachments of varying dimension and non-simplicial decompositions, enhancing adaptability in topological classification. For computational tasks requiring explicit geometry, polyhedra are preferable, whereas CW complexes excel in theoretical contexts demanding abstract homotopy-theoretic tools.
Polyhedron Infographic
 libterm.com
libterm.com