The Cartier operator plays a crucial role in algebraic geometry by acting on differential forms in characteristic p, enabling the study of Frobenius morphisms and their impact on cohomology. Its applications extend to analyzing the structure of algebraic curves and their moduli in positive characteristic fields, offering deep insights into arithmetic geometry. Explore the rest of the article to understand how the Cartier operator influences modern mathematical research and your studies in the field.
Table of Comparison
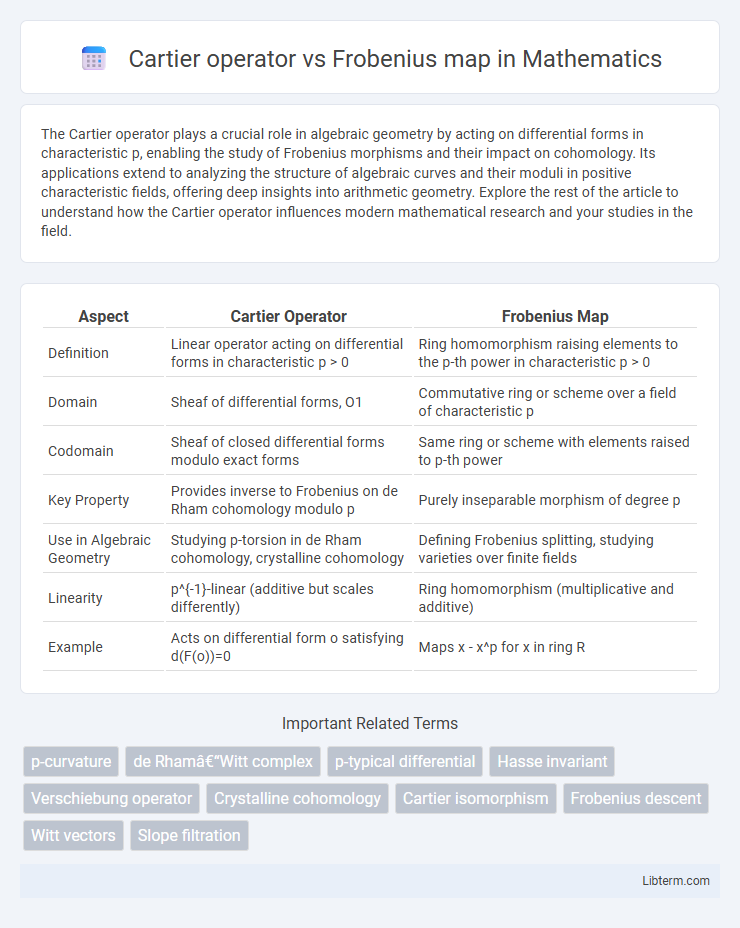
| Aspect | Cartier Operator | Frobenius Map |
|---|---|---|
| Definition | Linear operator acting on differential forms in characteristic p > 0 | Ring homomorphism raising elements to the p-th power in characteristic p > 0 |
| Domain | Sheaf of differential forms, O1 | Commutative ring or scheme over a field of characteristic p |
| Codomain | Sheaf of closed differential forms modulo exact forms | Same ring or scheme with elements raised to p-th power |
| Key Property | Provides inverse to Frobenius on de Rham cohomology modulo p | Purely inseparable morphism of degree p |
| Use in Algebraic Geometry | Studying p-torsion in de Rham cohomology, crystalline cohomology | Defining Frobenius splitting, studying varieties over finite fields |
| Linearity | p^{-1}-linear (additive but scales differently) | Ring homomorphism (multiplicative and additive) |
| Example | Acts on differential form o satisfying d(F(o))=0 | Maps x - x^p for x in ring R |
Introduction to Cartier Operator and Frobenius Map
The Cartier operator is a p-linear operator acting on differential forms in characteristic p, capturing the failure of the Frobenius pullback to be exact. The Frobenius map, a fundamental endomorphism in algebraic geometry over fields of characteristic p, raises coordinates to the p-th power and induces a morphism on schemes. Both concepts are central to understanding the structure of algebraic varieties in positive characteristic and their cohomological properties.
Historical Context in Algebraic Geometry
The Cartier operator, introduced by Pierre Cartier in the 1950s, emerged as a pivotal tool in the study of p-forms and crystalline cohomology within algebraic geometry over fields of positive characteristic. The Frobenius map, dating back to Ferdinand Frobenius's work in the late 19th and early 20th centuries, is a fundamental endomorphism acting on varieties in characteristic p, influencing their arithmetic and geometric structure. The interaction between the Cartier operator and the Frobenius map catalyzed advancements in understanding de Rham cohomology's behavior under inseparable morphisms, shaping modern perspectives on characteristic p geometry.
Definition of the Cartier Operator
The Cartier operator is a p-linear endomorphism acting on the sheaf of differential forms in characteristic p > 0, providing a splitting of the de Rham complex after Frobenius pullback. It serves as an inverse (up to twist) to the Frobenius map on differential forms, enabling the study of the crystalline cohomology and the reduction of algebraic varieties over finite fields. This operator extracts the part of a differential form that remains invariant under the Frobenius morphism, crucial for understanding the structure of de Rham cohomology in positive characteristic.
Definition of the Frobenius Map
The Frobenius map is an endomorphism of a ring of characteristic p, defined by raising each element to its p-th power, i.e., \( F(x) = x^p \). It plays a fundamental role in algebraic geometry and number theory, especially over fields of positive characteristic, where it interacts with the structure of schemes and cohomological operations. The Cartier operator serves as a sort of inverse, acting on differential forms by reversing the Frobenius pullback under certain conditions.
Key Properties of the Cartier Operator
The Cartier operator is a p^{-1}-linear map acting on the de Rham complex of varieties in characteristic p, crucial for studying the structure of differential forms modulo p. It serves as a left inverse to the Frobenius pullback on differential forms, satisfying the property C(F^*o) = o for forms o in the relevant cohomology groups. This operator preserves the Hodge filtration and plays a fundamental role in crystalline cohomology and the analysis of singularities in algebraic geometry over finite fields.
Fundamental Characteristics of the Frobenius Map
The Frobenius map is a ring homomorphism in characteristic p rings, raising each element to its p-th power, and it plays a crucial role in algebraic geometry and number theory. It is fundamental because it preserves the algebraic structure while interacting non-trivially with the cohomology of varieties over finite fields. Unlike the Cartier operator, which acts as a differential operator inverse on the de Rham complex, the Frobenius map drives the arithmetic and geometric properties through its endomorphism behavior on schemes in characteristic p.
Relationship Between Cartier Operator and Frobenius Map
The Cartier operator acts as a quasi-inverse to the Frobenius map on the de Rham complex of smooth varieties in characteristic p, providing a decomposition of differential forms modulo p. While the Frobenius map raises elements to their p-th powers, the Cartier operator extracts p-th roots at the level of differential forms, revealing deep structural insights in crystalline cohomology. This interplay plays a crucial role in understanding the behavior of algebraic varieties over fields of positive characteristic.
Applications in Positive Characteristic Fields
The Cartier operator and Frobenius map are fundamental tools in algebraic geometry over fields of positive characteristic, crucial for studying de Rham cohomology and crystalline cohomology. The Frobenius map acts by raising coordinates to the p-th power, providing a pivotal structure in the classification of algebraic varieties and their morphisms under characteristic p. The Cartier operator serves as a right inverse to the Frobenius action on differential forms, enabling the decomposition of de Rham complexes and facilitating the analysis of Hodge filtration and p-curvature phenomena in positive characteristic settings.
Comparative Analysis: Cartier Operator vs Frobenius Map
The Cartier operator acts on differential forms in characteristic p, providing a splitting of the Frobenius pullback on de Rham cohomology, while the Frobenius map itself is a ring homomorphism raising elements to their p-th power in characteristic p fields. The Cartier operator is semilinear and reduces the degree of differential forms, contrasting with the Frobenius map's purely multiplicative nature on the algebraic structure. This interplay is fundamental in algebraic geometry and arithmetic geometry, influencing the study of crystalline cohomology and p-adic Hodge theory.
Future Research and Open Problems
Future research on the Cartier operator and Frobenius map aims to deepen understanding of their interplay in positive characteristic geometry, particularly within crystalline cohomology and p-adic Hodge theory. Open problems include characterizing the precise algebraic and geometric conditions under which these operators commute or exhibit compatibility, and exploring their roles in the moduli spaces of vector bundles with connection. Advances in computational methods and novel categorical frameworks hold promise for resolving conjectures related to their spectral behavior and lifting properties in mixed characteristic settings.
Cartier operator Infographic
 libterm.com
libterm.com