The dot product is a fundamental algebraic operation that takes two equal-length sequences of numbers (vectors) and returns a single scalar value by multiplying corresponding entries and summing the results. It is widely used in physics, engineering, and computer graphics to determine the angle between vectors or project one vector onto another. Discover how understanding the dot product can enhance Your ability to solve complex problems by reading the rest of this article.
Table of Comparison
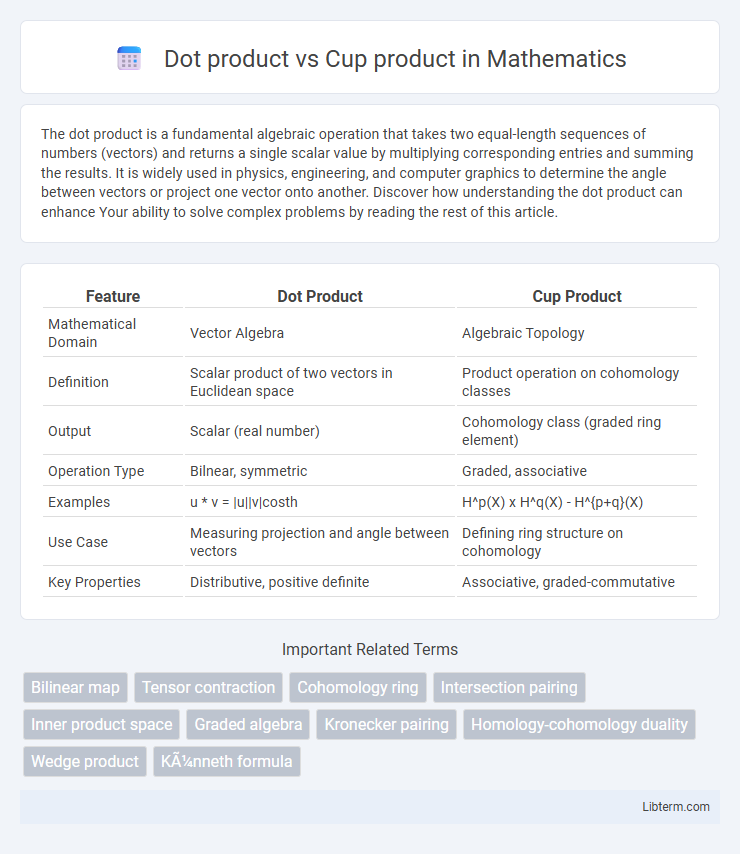
| Feature | Dot Product | Cup Product |
|---|---|---|
| Mathematical Domain | Vector Algebra | Algebraic Topology |
| Definition | Scalar product of two vectors in Euclidean space | Product operation on cohomology classes |
| Output | Scalar (real number) | Cohomology class (graded ring element) |
| Operation Type | Bilnear, symmetric | Graded, associative |
| Examples | u * v = |u||v|costh | H^p(X) x H^q(X) - H^{p+q}(X) |
| Use Case | Measuring projection and angle between vectors | Defining ring structure on cohomology |
| Key Properties | Distributive, positive definite | Associative, graded-commutative |
Introduction to Dot Product and Cup Product
Dot product is an algebraic operation that takes two equal-length sequences of numbers (usually vectors) and returns a single scalar value representing their geometric projection or similarity. Cup product is a fundamental operation in algebraic topology, combining cohomology classes to form new classes, providing a graded ring structure on cohomology groups. While the dot product arises in linear algebra and Euclidean geometry, the cup product plays a crucial role in understanding topological spaces through cohomology theory.
Mathematical Foundations
The dot product is a bilinear operation between two vectors in an inner product space, producing a scalar that measures their geometric alignment and magnitude projection. The cup product arises in cohomology theory as an associative graded-commutative product combining cohomology classes, reflecting topological space structures through algebraic invariants. While the dot product is foundational in linear algebra and Euclidean geometry, the cup product plays a crucial role in algebraic topology, linking cochain complexes to ring structures on cohomology groups.
Definitions and Notations
The dot product, denoted as \( \mathbf{a} \cdot \mathbf{b} \), is an algebraic operation that takes two vectors in Euclidean space and returns a scalar, calculated as the sum of the products of their corresponding components. The cup product, represented as \( \smile \), is a bilinear operation used in cohomology theory, combining cochains to produce a new cochain of higher degree, crucial for defining the ring structure on cohomology groups. While the dot product operates on vectors in \(\mathbb{R}^n\), the cup product acts on elements of cochain complexes \( C^p(X; G) \times C^q(X; G) \to C^{p+q}(X; G) \), where \(X\) is a topological space and \(G\) is a coefficient group.
Key Differences: Algebraic vs Topological
The dot product is an algebraic operation in vector spaces that takes two vectors and returns a scalar, encapsulating magnitude and directional alignment. The cup product, rooted in algebraic topology, combines cohomology classes to form a ring structure reflecting the topological features of a space. Key differences lie in their domains and outputs: the dot product operates in linear algebra producing scalars, while the cup product functions in cohomology, yielding new cohomology classes that capture topological information.
Applications in Mathematics and Physics
The dot product, a scalar product of two vectors, is fundamental in physics for calculating work, projections, and determining angles between vectors in Euclidean spaces. The cup product, an operation in cohomology theory, plays a crucial role in algebraic topology by enabling the construction of ring structures on cohomology groups, facilitating classification of topological spaces. Both products serve distinct purposes; the dot product aids in quantitative physical analysis, while the cup product provides algebraic tools for studying topological invariants.
Geometric Interpretation
The dot product represents the scalar projection of one vector onto another, measuring the magnitude of one vector in the direction of the other and resulting in a scalar that quantifies their alignment or angle. The cup product in algebraic topology combines cohomology classes, reflecting intersection properties of spaces and higher-dimensional analogs, and produces a new cohomology class that encodes how subspaces intersect or overlap. Geometrically, the dot product corresponds to measuring directional similarity in Euclidean space, while the cup product captures complex topological relationships within a space's structure.
Properties and Theorems
The dot product is a bilinear, symmetric operation producing a scalar, satisfying properties such as linearity in each argument and positive-definiteness, making it fundamental in defining inner product spaces. The cup product, defined in cohomology theory, is an associative and graded-commutative operation that combines cohomology classes, adhering to properties like distributivity and naturality, and plays a key role in the ring structure of cohomology groups. Important theorems include the Hodge decomposition relating the dot product to harmonic forms and the Kunneth formula connecting the behavior of the cup product on product spaces.
Computation Methods
The dot product is computed by multiplying corresponding components of two vectors and summing the results, yielding a scalar that represents their directional similarity. The cup product, used in algebraic topology, combines cohomology classes via an operation on chain complexes, resulting in an element of higher degree in the cohomology ring. Computationally, the dot product involves straightforward linear algebraic operations, while the cup product requires complex chain-level maps and boundary operator manipulations to determine the product in cohomology.
Common Misconceptions
The dot product and cup product are often confused due to their similar-sounding names but represent fundamentally different operations in mathematics; the dot product is an algebraic operation between two vectors resulting in a scalar, whereas the cup product is a cohomological operation in algebraic topology used to combine cohomology classes. A common misconception is treating the cup product as simply a vector operation like the dot product, ignoring its richer topological and algebraic structure that encodes interactions between spaces. Unlike the dot product, the cup product is associative and graded-commutative, properties that are essential in the study of algebraic topology but not relevant to the scalar results of dot products in linear algebra.
Summary and Comparative Analysis
The dot product and cup product serve distinct roles in mathematics: the dot product calculates a scalar from two vectors in Euclidean space, while the cup product is an operation in cohomology that combines cochains to form higher-dimensional cohomology classes. The dot product is fundamental in linear algebra and geometry for measuring angles and projections, whereas the cup product is critical in algebraic topology for constructing the cohomology ring of a topological space. Their comparative analysis highlights the dot product's role in vector spaces versus the cup product's function in abstract algebraic structures associated with topological invariants.
Dot product Infographic
 libterm.com
libterm.com