Real numbers form the foundation of mathematics, representing all the values along the continuous number line including both rational and irrational numbers. These numbers are essential in various fields such as engineering, physics, and finance, where accurate measurement and calculation are crucial. Discover how understanding real numbers can enhance your problem-solving skills by reading the rest of this article.
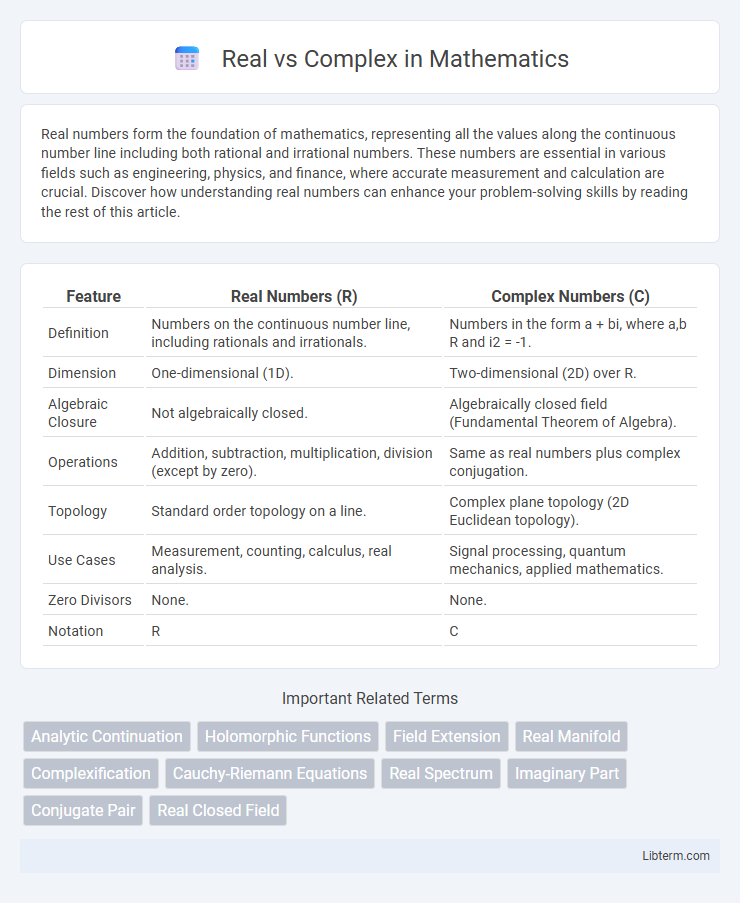
Table of Comparison
| Feature | Real Numbers (R) | Complex Numbers (C) |
|---|---|---|
| Definition | Numbers on the continuous number line, including rationals and irrationals. | Numbers in the form a + bi, where a,b R and i2 = -1. |
| Dimension | One-dimensional (1D). | Two-dimensional (2D) over R. |
| Algebraic Closure | Not algebraically closed. | Algebraically closed field (Fundamental Theorem of Algebra). |
| Operations | Addition, subtraction, multiplication, division (except by zero). | Same as real numbers plus complex conjugation. |
| Topology | Standard order topology on a line. | Complex plane topology (2D Euclidean topology). |
| Use Cases | Measurement, counting, calculus, real analysis. | Signal processing, quantum mechanics, applied mathematics. |
| Zero Divisors | None. | None. |
| Notation | R | C |
Understanding Real Numbers
Real numbers encompass all rational and irrational numbers representing points on the continuous number line, including integers, fractions, and non-repeating decimals. Understanding real numbers is fundamental in mathematical analysis and geometry, as they allow precise measurement and representation of quantities in both theoretical and applied contexts. Real numbers differ from complex numbers, which include an imaginary component represented by the unit "i," where i2 = -1, expanding the number system to solve equations with no real roots.
Defining Complex Numbers
Complex numbers extend the real number system by incorporating an imaginary unit, denoted as \( i \), where \( i^2 = -1 \). A complex number is expressed in the form \( a + bi \), with \( a \) representing the real part and \( b \) the imaginary part. This definition allows for the representation and manipulation of numbers beyond the one-dimensional real number line, enabling solutions to equations that have no real roots.
Key Differences: Real vs Complex Numbers
Real numbers include all rational and irrational numbers that lie on the number line, expressed as decimals or fractions without an imaginary part. Complex numbers consist of a real part and an imaginary part, typically written as a + bi, where "a" and "b" are real numbers and "i" represents the square root of -1. Key differences involve arithmetic properties; real numbers are ordered and lie on a one-dimensional number line, while complex numbers exist in a two-dimensional plane, making them non-orderable but suitable for solving polynomial equations lacking real solutions.
Properties of Real Numbers
Real numbers possess properties such as closure under addition, subtraction, multiplication, and division (excluding division by zero), making them a complete ordered field. They adhere to the commutative, associative, and distributive properties, facilitating consistent algebraic manipulation. Unlike complex numbers, real numbers can be represented on a one-dimensional number line, providing a natural order relation and enabling comparison between magnitudes.
Properties of Complex Numbers
Complex numbers consist of a real part and an imaginary part, often expressed as a + bi, where a and b are real numbers and i is the imaginary unit with the property i2 = -1. They exhibit unique properties such as being closed under addition, subtraction, multiplication, and division (except division by zero), unlike real numbers where certain operations may lead outside the set of real numbers. The magnitude (or modulus) of a complex number is calculated as (a2 + b2), and its conjugate, a - bi, plays a crucial role in simplifying division and solving polynomial equations.
Operations with Real and Complex Numbers
Operations with real numbers involve basic arithmetic such as addition, subtraction, multiplication, and division within the set of all rational and irrational numbers on the number line. Complex number operations extend these concepts by incorporating imaginary units, where addition and subtraction combine real and imaginary parts separately, and multiplication and division use the distributive property alongside the imaginary unit squared (i2 = -1). The ability to perform these operations on complex numbers is essential in fields like electrical engineering and quantum mechanics, where real and imaginary components represent different dimensions of physical phenomena.
Geometric Representation
Real numbers are represented geometrically on a one-dimensional number line, where each point corresponds to a specific value with magnitude and sign. Complex numbers extend this representation to a two-dimensional plane, known as the complex plane or Argand diagram, where the horizontal axis denotes the real part and the vertical axis indicates the imaginary part. This geometric framework allows visualization of complex number operations such as addition, subtraction, and multiplication through vector addition and rotation.
Applications in Mathematics and Engineering
Real numbers are essential in calculus, algebra, and real analysis, forming the basis for problems involving measurements, rates of change, and real-valued functions in engineering and physics. Complex numbers extend these applications by enabling solutions in electrical engineering, control systems, and signal processing through their representation of oscillations and waveforms in the complex plane. The use of complex analysis allows for more comprehensive problem-solving approaches in both theoretical mathematics and practical engineering design challenges.
Advantages and Limitations
Real numbers offer simplicity and efficiency in computations, making them ideal for applications requiring straightforward arithmetic and easy interpretation, such as measurement and basic engineering tasks. Complex numbers provide powerful tools for solving problems involving oscillations, waves, and electrical engineering by enabling representation of both magnitude and phase. However, real numbers are limited in representing phenomena with multiple dimensions or non-real solutions, while complex numbers involve more computational complexity and may require specialized understanding for practical implementation.
Summary: Choosing Real or Complex Numbers
Real numbers represent quantities along a continuous number line, ideal for measuring tangible values such as distance, weight, and time. Complex numbers incorporate both real and imaginary parts, enabling solutions to equations lacking real roots and facilitating advanced engineering, physics, and signal processing tasks. Selecting real or complex numbers depends on the problem's nature: real numbers suit straightforward calculations, while complex numbers handle multidimensional phenomena and abstract mathematical models.
Real Infographic
 libterm.com
libterm.com