Setting a lower limit ensures that minimum requirements are consistently met, preventing underperformance and maintaining quality standards in various processes. This threshold acts as a safeguard, helping you avoid risks associated with insufficient levels in measurements, finances, or production. Explore the rest of the article to understand how establishing lower limits can optimize your operations effectively.
Table of Comparison
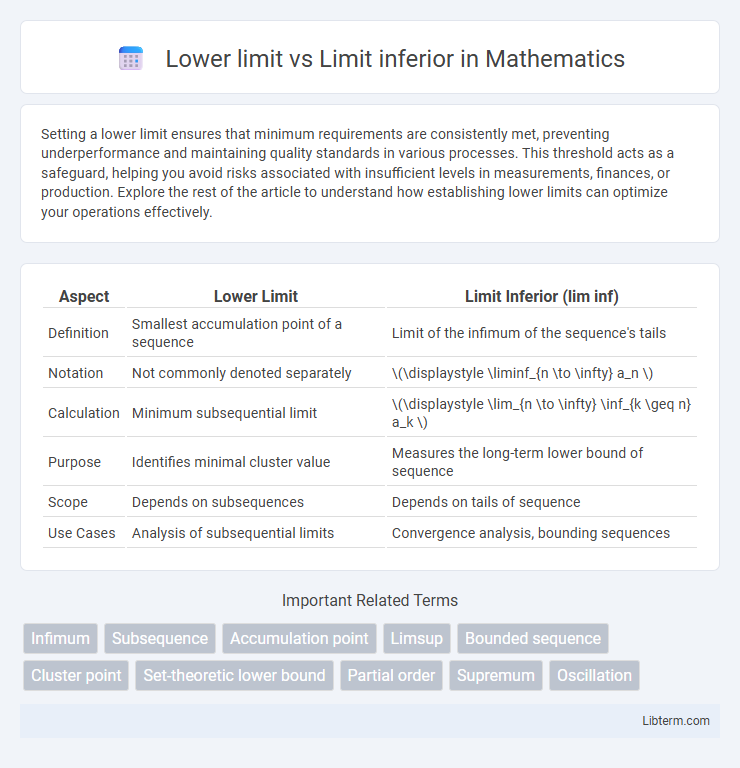
| Aspect | Lower Limit | Limit Inferior (lim inf) |
|---|---|---|
| Definition | Smallest accumulation point of a sequence | Limit of the infimum of the sequence's tails |
| Notation | Not commonly denoted separately | \(\displaystyle \liminf_{n \to \infty} a_n \) |
| Calculation | Minimum subsequential limit | \(\displaystyle \lim_{n \to \infty} \inf_{k \geq n} a_k \) |
| Purpose | Identifies minimal cluster value | Measures the long-term lower bound of sequence |
| Scope | Depends on subsequences | Depends on tails of sequence |
| Use Cases | Analysis of subsequential limits | Convergence analysis, bounding sequences |
Understanding the Concepts: Lower Limit vs Limit Inferior
The lower limit of a sequence is the smallest accumulation point or the infimum of the set of subsequential limits, providing a measure of the sequence's minimal long-term behavior. The limit inferior, often denoted as lim inf, formalizes this concept by representing the limit of the sequence of infimums of the tails of the sequence, capturing the minimal values the sequence approaches infinitely often. Understanding the distinction between lower limit and limit inferior is crucial for analyzing convergence properties and oscillatory behaviors in mathematical sequences.
Defining Lower Limit in Mathematical Terms
The lower limit of a sequence, often called the limit inferior (lim inf), is defined as the greatest lower bound of the set of all subsequential limits, capturing the smallest accumulation point. Mathematically, for a sequence (a_n), the lower limit is expressed as lim inf a_n = lim (n-) inf {a_k : k >= n}. This concept ensures that the sequence does not fall below this boundary infinitely often, serving as a fundamental tool in real analysis for understanding sequence convergence behavior.
What Is Limit Inferior (lim inf)?
Limit inferior (lim inf) of a sequence is the greatest lower bound of its subsequential limits, capturing the long-term minimum values the sequence approaches. It is defined as the limit of the infimum of the tail sets of the sequence, mathematically expressed as lim inf a_n = lim (n-) inf {a_k : k >= n}. Unlike the lower limit, which often refers to a minimal bound in various contexts, the limit inferior provides precise characterization of a sequence's asymptotic lower behavior.
Key Differences Between Lower Limit and Limit Inferior
Lower limit and limit inferior are closely related concepts in mathematical analysis, often used in the context of sequences. The lower limit, also called the infimum limit, refers to the greatest lower bound of the set of subsequential limits of a sequence, while the limit inferior is defined formally as the limit of the infimums of the tails of the sequence. Key differences lie in their definitions and applications: the limit inferior is a limit process involving the infimum over the tail sets, whereas the lower limit emphasizes the smallest cluster point and is often used in order theory and topology.
Importance of Lower Limit in Real Analysis
Lower limit, often defined as the infimum of a sequence's tail subsequences, captures the minimal accumulation points necessary for understanding sequence convergence in real analysis. Limit inferior provides a precise measure of the smallest limit value a sequence approaches infinitely often, essential for characterizing boundedness and convergence properties in metric spaces. Emphasizing the lower limit enables rigorous analysis of function behavior, aiding in the study of monotonicity and oscillatory behavior within advanced calculus and real analysis frameworks.
Applications of Limit Inferior in Sequences
Limit inferior, or lim inf, of a sequence is the greatest lower bound of its set of subsequential limits, providing crucial insights into the sequence's long-term behavior and stability. Applications of limit inferior include analyzing convergence in real analysis, determining oscillatory behavior in bounded sequences, and establishing criteria for almost sure convergence in probability theory. In dynamical systems, lim inf helps identify invariant sets and equilibrium points, while in optimization, it assists in evaluating the limiting behavior of iterative algorithms.
Visualizing Lower Limit and Limit Inferior
Visualizing the lower limit involves examining the smallest subsequential values a sequence approaches, highlighting points where the sequence eventually stays above certain thresholds. The limit inferior, or lim inf, captures the greatest lower bound of these subsequential limits, representing the "long-term" minimum behavior of the sequence. Graphically, the lower limit can be seen as the limit of the infimum of the tails of the sequence, forming a non-decreasing step-like visualization approaching the lim inf.
Common Misconceptions and Errors
Lower limit is often confused with limit inferior, but the lower limit typically refers to the minimum value within a set, while the limit inferior concerns the limit of the infimum of a sequence as it progresses to infinity. A common error is assuming the lower limit and limit inferior are interchangeable terms, leading to misinterpretations in convergence analysis. Clarifying that the limit inferior captures long-term behavior in sequences helps in avoiding mistakes in mathematical proofs and applications.
Lower Limit vs Limit Inferior: Practical Examples
Lower limit and limit inferior both describe boundary behavior of sequences, but the lower limit refers to the greatest lower bound of the set of subsequential limits, while the limit inferior identifies the limit of the sequence's infimum over all tail segments. For example, given the sequence a_n = (-1)^n + 1/n, the lower limit is -1 since subsequences approach -1, whereas the limit inferior is also -1 representing the lowest cluster point in the tail. In practical analysis, the lower limit provides insight into subsequential bounds, whereas the limit inferior is essential for understanding the asymptotic minimal behavior of oscillating sequences.
Summary and Final Thoughts
Lower limit and limit inferior both describe the smallest accumulation points of a sequence, but limit inferior specifically refers to the limit of the sequence of infima of tail subsequences. The lower limit highlights immediate minimum bounds, while the limit inferior captures overall subsequential behavior across infinite terms. Understanding their distinction clarifies convergence properties and aids in analyzing sequence limits and boundedness in real analysis.
Lower limit Infographic
 libterm.com
libterm.com