Bounded concepts are essential in mathematics and computer science, referring to limits within which values or functions operate. Understanding bounded systems helps you analyze constraints and optimize solutions in areas like algorithms, data structures, and real-world problem-solving. Explore the rest of this article to uncover detailed examples and applications of bounded principles.
Table of Comparison
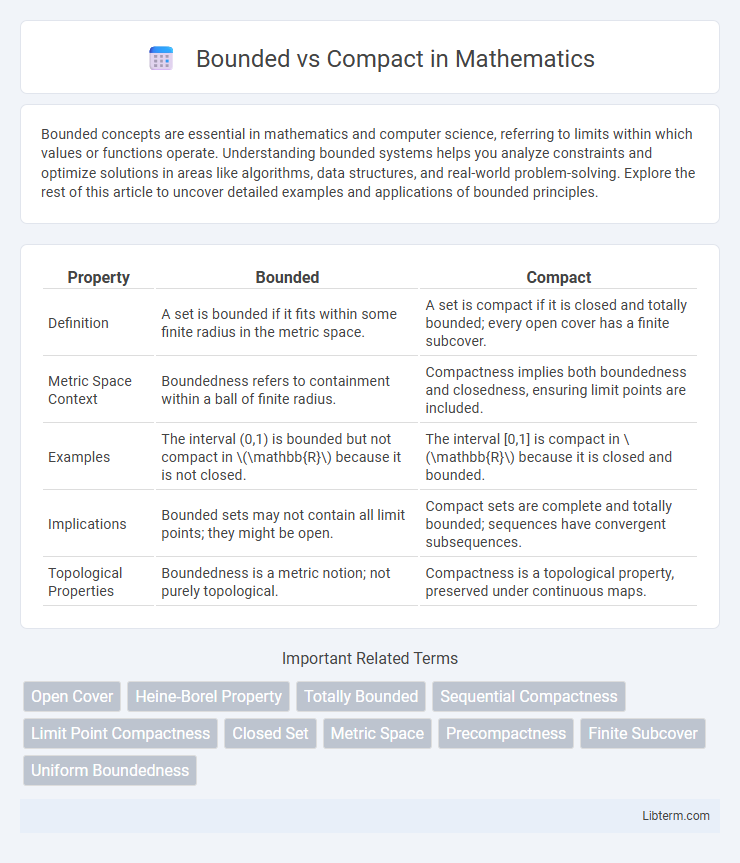
| Property | Bounded | Compact |
|---|---|---|
| Definition | A set is bounded if it fits within some finite radius in the metric space. | A set is compact if it is closed and totally bounded; every open cover has a finite subcover. |
| Metric Space Context | Boundedness refers to containment within a ball of finite radius. | Compactness implies both boundedness and closedness, ensuring limit points are included. |
| Examples | The interval (0,1) is bounded but not compact in \(\mathbb{R}\) because it is not closed. | The interval [0,1] is compact in \(\mathbb{R}\) because it is closed and bounded. |
| Implications | Bounded sets may not contain all limit points; they might be open. | Compact sets are complete and totally bounded; sequences have convergent subsequences. |
| Topological Properties | Boundedness is a metric notion; not purely topological. | Compactness is a topological property, preserved under continuous maps. |
Understanding Bounded Sets
Bounded sets in a metric space are those contained within some fixed radius ball, ensuring all points lie within a finite distance from a central point. Understanding boundedness is crucial for analyzing the size and limits of sets, especially in contrast with compact sets, which are both bounded and closed. This distinction underpins many fundamental theorems in analysis and topology, such as Heine-Borel, highlighting that boundedness alone does not guarantee compactness without closure.
Defining Compact Sets
Compact sets in topology are defined as those that are both closed and bounded in Euclidean spaces, ensuring every open cover has a finite subcover. Unlike merely bounded sets, compact sets guarantee properties like sequential compactness and limit point containment, which are essential for continuity and convergence analysis. The Heine-Borel theorem specifically characterizes compact subsets of Euclidean spaces by this intersection of closedness and boundedness.
Key Differences: Boundedness vs. Compactness
Boundedness refers to a set being contained within some finite region, meaning all its points lie within a fixed distance from a central reference, while compactness requires a set to be both closed and bounded, ensuring that every open cover has a finite subcover. In metric spaces, compact sets are always bounded, but bounded sets need not be compact unless the space is complete and closed conditions are met. The key difference lies in compactness guaranteeing limit point inclusion and finite subcover existence, properties not ensured by mere boundedness.
The Role of Topology in Compactness
Topology plays a crucial role in understanding compactness, distinguishing it from mere boundedness by emphasizing the structure of open covers rather than size constraints. Compactness requires every open cover to have a finite subcover, a property deeply tied to the topological space's open sets and continuity, unlike boundedness, which relies solely on metric constraints. Consequently, compactness serves as a powerful topological invariant, often implying boundedness in metric spaces but extending far beyond through its intrinsic topological definition.
Examples of Bounded but Not Compact Sets
In metric spaces, the set of rational numbers within the interval [0,1] is bounded but not compact due to lack of completeness. The open interval (0,1) in the real numbers is bounded but fails to be compact because it is not closed, allowing sequences to escape the set's closure. Similarly, the set of points {(x, sin(1/x)) : x (0,1]} in R2 is bounded but not compact, as it lacks limit points at x=0, highlighting the necessity of closedness for compactness in Euclidean spaces.
Real-World Applications of Compact Sets
Compact sets have crucial applications in optimization, where the existence of maximum and minimum values on closed and bounded domains ensures solution feasibility in engineering and economics. In control theory, compactness guarantees system stability by confining trajectories within manageable boundaries, crucial for robotics navigation and automated systems. Furthermore, compact sets facilitate numerical methods in computer graphics, enabling efficient rendering algorithms by exploiting their finiteness and limiting behaviors.
The Heine-Borel Theorem Explained
The Heine-Borel Theorem characterizes compact subsets of Euclidean space as those that are both closed and bounded, illustrating a precise relationship between boundedness and compactness. In \(\mathbb{R}^n\), a set is compact if every open cover has a finite subcover, ensuring properties like sequential compactness and limit point inclusion. This theorem distinguishes compact sets from merely bounded sets by emphasizing closure, making it a cornerstone in real analysis and topology.
Counterexamples: Compact Without Boundedness
A classic counterexample illustrating compactness without boundedness arises in certain infinite-dimensional function spaces, such as the space of continuous functions on [0,1] with the topology of pointwise convergence, where compact sets need not be bounded in the norm topology. In metric spaces, compactness always implies boundedness, but this equivalence fails in general topological vector spaces, highlighting the subtle distinctions between these properties. Understanding this nuance is essential in functional analysis, especially when dealing with weak topologies or non-metric settings where compactness and boundedness diverge.
Compactness in Metric Spaces
In metric spaces, compactness is characterized by every open cover having a finite subcover, ensuring limit points exist within the set, which is stronger than mere boundedness that only restricts the set's diameter. Compact metric spaces are necessarily complete and totally bounded, meaning they can be covered by finitely many balls of any positive radius. This intrinsic link between compactness, completeness, and total boundedness differentiates compact sets from simply bounded ones in metric space topology.
Summary: Choosing Between Bounded and Compact
Bounded sets contain all points within a fixed distance but may lack completeness or closure, while compact sets are both closed and bounded, guaranteeing properties like limit point inclusion and compactness-related theorems. For practical applications in analysis and topology, compact sets are preferable due to their stronger structural characteristics, such as ensuring every open cover has a finite subcover. When choosing between bounded and compact, prioritize compactness for stability and convergence in metric spaces, but consider boundedness alone if closure or completeness conditions are not required.
Bounded Infographic
 libterm.com
libterm.com