Semimetric structures offer a balanced approach, combining symmetry with subtle asymmetry to create visual interest and functional design. Their unique properties make them ideal for applications in architecture, art, and product design, enhancing both aesthetics and usability. Explore the following article to discover how semimetric principles can transform your creative projects.
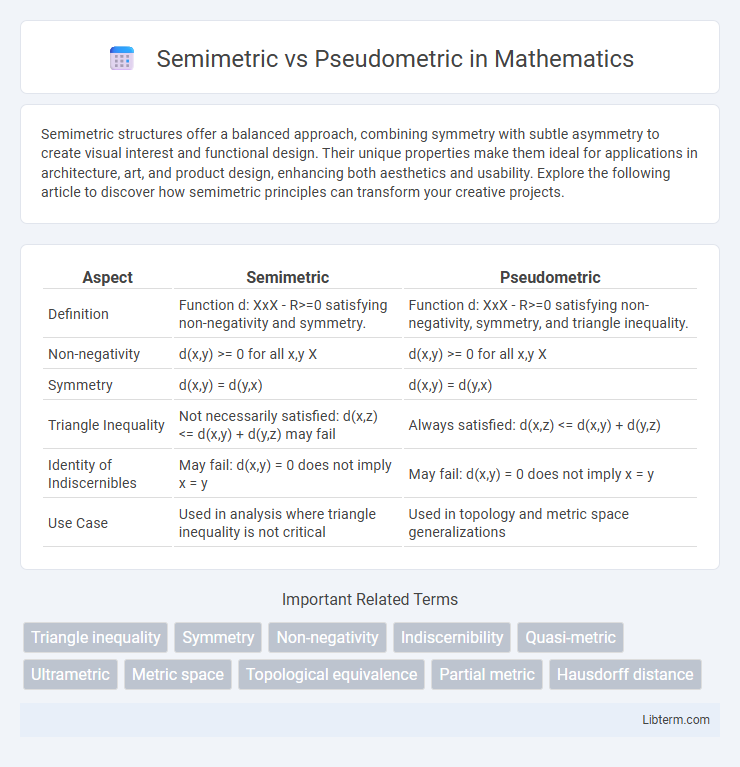
Table of Comparison
| Aspect | Semimetric | Pseudometric |
|---|---|---|
| Definition | Function d: XxX - R>=0 satisfying non-negativity and symmetry. | Function d: XxX - R>=0 satisfying non-negativity, symmetry, and triangle inequality. |
| Non-negativity | d(x,y) >= 0 for all x,y X | d(x,y) >= 0 for all x,y X |
| Symmetry | d(x,y) = d(y,x) | d(x,y) = d(y,x) |
| Triangle Inequality | Not necessarily satisfied: d(x,z) <= d(x,y) + d(y,z) may fail | Always satisfied: d(x,z) <= d(x,y) + d(y,z) |
| Identity of Indiscernibles | May fail: d(x,y) = 0 does not imply x = y | May fail: d(x,y) = 0 does not imply x = y |
| Use Case | Used in analysis where triangle inequality is not critical | Used in topology and metric space generalizations |
Introduction to Generalized Metrics
Semimetrics relax the symmetry requirement found in traditional metrics, allowing distance functions d(x, y) d(y, x), while pseudometrics permit distinct points to have zero distance, i.e., d(x, y) = 0 for x y, generalizing metric space concepts. These generalized metrics enable analysis in asymmetric spaces and improve clustering or similarity measures where symmetry or identity of indiscernibles may fail. The study of semimetric and pseudometric spaces expands applications in machine learning, network theory, and topology by accommodating more flexible distance definitions.
Defining Semimetric Spaces
Semimetric spaces are defined by a distance function that satisfies non-negativity and identity of indiscernibles but may lack symmetry and the triangle inequality, differentiating them from pseudometric spaces which require symmetry and the triangle inequality. In semimetric spaces, the distance between two points can be zero even if the points are distinct, similar to pseudometrics, but the absence of symmetry allows d(x, y) d(y, x). This relaxed structure enables modeling of asymmetric relationships in data analysis and computer science where traditional metric properties do not hold.
Understanding Pseudometric Spaces
Pseudometric spaces generalize metric spaces by allowing distinct points to have zero distance, meaning d(x, y) = 0 does not imply x = y, unlike in semimetric spaces where the triangle inequality or symmetry may fail. Understanding pseudometric spaces involves studying their relaxed distance functions that retain non-negativity, symmetry, and the triangle inequality but permit indiscernibles, making them crucial in functional analysis and topology. These spaces facilitate the analysis of equivalence classes and quotient spaces by identifying points at zero pseudodistance, broadening the scope of metric space applications.
Key Differences: Semimetric vs Pseudometric
Semimetrics differ from pseudometrics primarily in the relaxation of the triangle inequality, where semimetrics do not require it to hold, while pseudometrics enforce a generalized form of the triangle inequality. Unlike semimetrics, pseudometrics allow distinct points to have zero distance but still maintain symmetry and the triangle inequality. The key distinction lies in the adherence to metric space axioms: pseudometrics closely mimic metrics except for distinct zero distances, whereas semimetrics broaden the concept by relaxing one or more metric conditions.
Mathematical Properties of Semimetrics
Semimetrics generalize metrics by relaxing the triangle inequality, allowing d(x, x) = 0 without requiring d(x, y) > 0 for x y, unlike pseudometrics where symmetry and triangle inequality must hold. Semimetrics maintain non-negativity and identity of indiscernibles but may fail symmetry, impacting their topological and convergence properties. These mathematical properties enable semimetrics to model asymmetric relations and specialized distance-like functions in various applied settings.
Core Characteristics of Pseudometrics
Pseudometrics are distance functions that satisfy non-negativity, symmetry, and the triangle inequality but allow distinct points to have zero distance, unlike metrics. They play a crucial role in functional analysis and topology by relaxing the strict distinguishability condition found in metrics. This core characteristic enables the modeling of equivalence relations within metric spaces, making pseudometrics essential in the study of quotient spaces and convergence structures.
Real-World Examples and Applications
Semimetric spaces, which relax the triangle inequality, are useful in fields like psychology for modeling subjective similarities where perception distances don't strictly adhere to metric rules; for instance, in cognitive science, the perceived difference between stimuli may fail the triangle inequality. Pseudometric spaces, allowing zero distance between distinct points, are frequently applied in clustering algorithms and pattern recognition, such as in machine learning where objects in the same cluster have zero pairwise distance despite being distinct entities. Real-world applications include recommendation systems utilizing pseudometrics to group similar user preferences and computational biology employing semimetrics to represent genetic similarity measures that do not strictly conform to metric properties.
Importance in Topology and Analysis
Semimetrics and pseudometrics play crucial roles in topology and analysis by generalizing the concept of distance while relaxing the strict properties of metrics. Semimetrics omit symmetry or the triangle inequality, enabling the study of asymmetric or non-triangular structures in topological spaces, which is important in domains like domain theory and functional analysis. Pseudometrics allow distinct points to have zero distance, facilitating the construction of quotient spaces and the treatment of equivalence classes in analysis and metric topology.
Common Misconceptions and Pitfalls
Semimetric and pseudometric spaces are often confused due to their relaxed conditions compared to metrics, but a key misconception is that both satisfy the triangle inequality, whereas only pseudometrics do. Semimetrics drop the requirement of the triangle inequality, leading to potential pitfalls in applications like clustering or similarity measurement where this property ensures meaningful distance interpretation. Ignoring these distinctions can result in incorrect algorithm behavior or misinterpretation of data structures, particularly in machine learning and topological data analysis contexts.
Conclusion: Choosing Between Semimetric and Pseudometric
Choosing between semimetric and pseudometric depends on the specific requirements of distance properties in your analysis. Semimetrics relax the triangle inequality, allowing more flexibility in modeling dissimilarities without strict metric constraints, while pseudometrics maintain the triangle inequality but permit zero distances between distinct points. Prioritize pseudometrics for datasets needing metric-like reliability and semimetrics when capturing more generalized or asymmetric relationships is crucial.
Semimetric Infographic
 libterm.com
libterm.com