Functors are a fundamental concept in programming and category theory, acting as mappings between categories that preserve their structure. They enable the transformation of data while maintaining context, widely used in functional programming languages like Haskell to handle operations on containers or computational contexts. Explore the rest of the article to deepen your understanding of how functors facilitate powerful abstractions in software development.
Table of Comparison
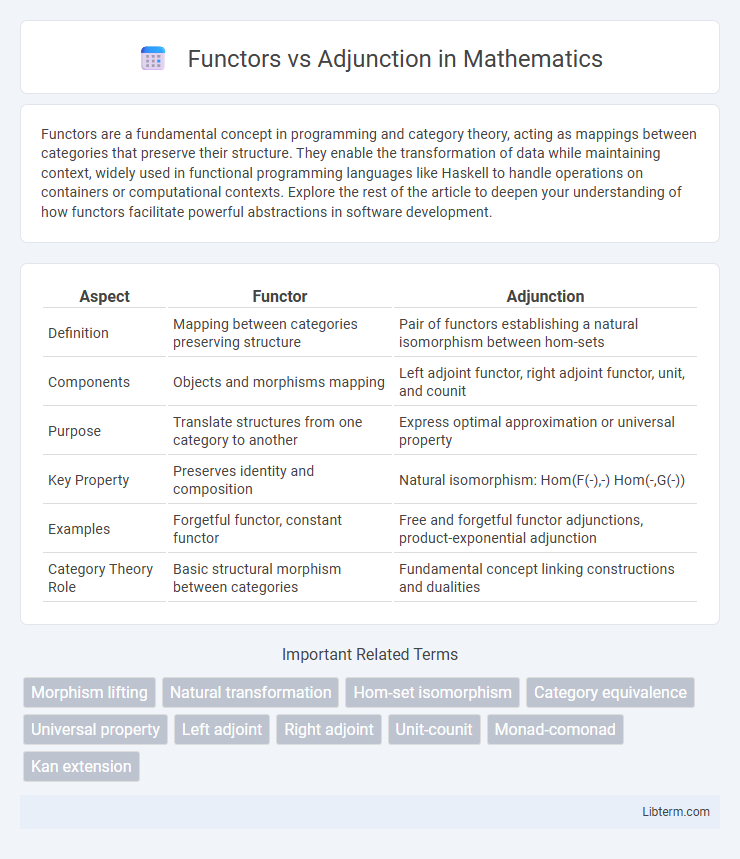
| Aspect | Functor | Adjunction |
|---|---|---|
| Definition | Mapping between categories preserving structure | Pair of functors establishing a natural isomorphism between hom-sets |
| Components | Objects and morphisms mapping | Left adjoint functor, right adjoint functor, unit, and counit |
| Purpose | Translate structures from one category to another | Express optimal approximation or universal property |
| Key Property | Preserves identity and composition | Natural isomorphism: Hom(F(-),-) Hom(-,G(-)) |
| Examples | Forgetful functor, constant functor | Free and forgetful functor adjunctions, product-exponential adjunction |
| Category Theory Role | Basic structural morphism between categories | Fundamental concept linking constructions and dualities |
Introduction to Functors and Adjunctions
Functors are structure-preserving mappings between categories, enabling the transfer of objects and morphisms while maintaining composition and identity. Adjunctions describe a paired relationship between two functors, capturing a fundamental connection through natural transformations known as unit and counit, which reflect a generalized form of inverse behavior. Understanding functors and adjunctions is essential for exploring categorical constructs and abstracting mathematical patterns in various domains.
Understanding Functors in Category Theory
Functors in category theory serve as structure-preserving mappings between categories, associating objects and morphisms in one category to objects and morphisms in another while maintaining composition and identity. They enable the translation of mathematical concepts across different contexts, facilitating comparisons and the transfer of properties. Understanding functors is fundamental for studying adjunctions, where pairs of functors exhibit a special relationship characterized by natural transformations and universal properties.
What Is an Adjunction?
An adjunction in category theory is a fundamental concept describing a pair of functors between two categories that stand in a specific relationship, called adjoint functors. One functor, called the left adjoint, maps objects from the first category to the second, while its right adjoint functor maps objects back, with a natural isomorphism relating hom-sets. This natural isomorphism encapsulates a precise way to transform morphisms involving these functors, revealing deep structural connections between categories beyond simple functorial mappings.
Key Differences: Functors vs Adjunctions
Functors map objects and morphisms between categories, preserving their structure, while adjunctions establish a pair of functors linked by a natural isomorphism between hom-sets, capturing a universal property. Functors act as category-to-category transformations, whereas adjunctions provide a framework for comparing these transformations bidirectionally through unit and counit natural transformations. Key distinctions lie in functors' role as structure-preserving maps versus adjunctions' role in expressing a fundamental relationship between two functors.
Functorial Examples in Mathematics
Functorial examples in mathematics include the fundamental group functor, which assigns to each topological space a group capturing its loop structure, and the homology functor, which maps topological spaces to sequences of abelian groups reflecting their geometric features. Another key example is the tensor product functor in category theory, linking modules over a ring through bilinear maps and revealing interactions between algebraic structures. These functors exemplify how mathematical objects and morphisms transform across categories, preserving essential properties and enabling deeper structural insights.
Real-World Applications of Adjunctions
Adjunctions play a crucial role in computer science by modeling the relationship between syntax and semantics, such as in type theory where free functors and forgetful functors form adjoint pairs to simplify program reasoning. In category theory applied to database theory, adjunctions enable data migration between schemas through left and right adjoints, facilitating query optimization and data integration. Moreover, in quantum computing, adjoint functors underpin the construction of dualities, supporting the development of reversible computations and error correction codes.
How Adjunctions Relate to Functors
Adjunctions establish a fundamental relationship between pairs of functors, typically a left adjoint and a right adjoint, connecting categories via natural transformations called unit and counit. These natural transformations create a bijection between hom-sets, meaning the process of mapping objects and morphisms in one category aligns precisely with the reverse mapping in another, governed by the adjunction. This interplay enables functors to reflect and preserve structural properties, making adjunctions essential for understanding equivalences and constructions in category theory.
Importance of Functors and Adjunctions in Algebra
Functors serve as essential tools in algebra for mapping objects and morphisms between categories, preserving structural relationships and enabling seamless translation of properties across different algebraic contexts. Adjunctions establish a fundamental link between pairs of functors, capturing universal constructions such as free objects and forgetful functors, which are central to understanding categorical equivalences and dualities in algebra. The interplay of functors and adjunctions facilitates the abstraction and generalization of algebraic concepts, driving advances in fields like module theory, homological algebra, and representation theory.
Common Misconceptions about Functors and Adjunctions
Functors are often misunderstood as simply structure-preserving maps between categories, but they also capture deeper transformations linking mathematical contexts, while adjunctions describe a pair of functors with a tight, reciprocal relationship that generalizes universal constructions. A common misconception is that all functors have adjoints; however, adjoints exist only under specific conditions related to limits, colimits, or representability. Misinterpreting adjunctions as mere equivalences overlooks their role in establishing fundamental correspondences that underpin constructions like free objects and hom-set isomorphisms.
Conclusion: Choosing Between Functors and Adjunctions
Choosing between functors and adjunctions depends on the complexity and goals of the category-theoretic framework being employed. Functors serve as basic structure-preserving maps between categories, suitable for straightforward transformations, while adjunctions provide a deeper relationship that encapsulates universal properties and dualities. Leveraging adjunctions enables more powerful abstractions and connections between categories, making them essential for advanced categorical constructions and equivalences.
Functors Infographic
 libterm.com
libterm.com