Cocountable is a versatile term often used in mathematics and logic to describe sets whose complements are countable, meaning they have a finite or countably infinite number of elements missing. Understanding cocountable sets can help you grasp key concepts in topology and measure theory, where these sets play a crucial role in defining certain types of spaces and functions. Explore the rest of the article to deepen your knowledge of cocountable sets and their applications.
Table of Comparison
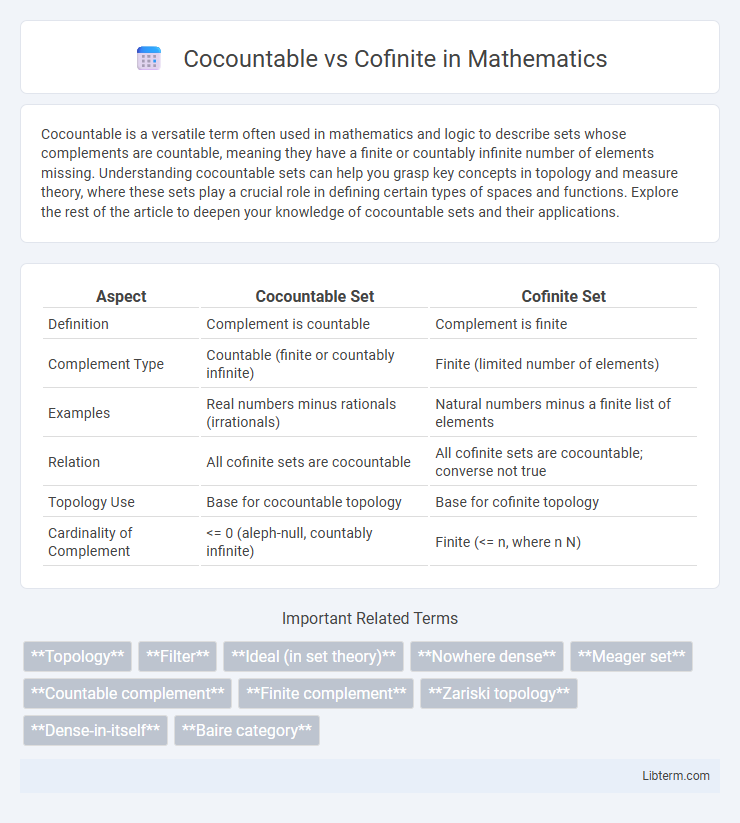
| Aspect | Cocountable Set | Cofinite Set |
|---|---|---|
| Definition | Complement is countable | Complement is finite |
| Complement Type | Countable (finite or countably infinite) | Finite (limited number of elements) |
| Examples | Real numbers minus rationals (irrationals) | Natural numbers minus a finite list of elements |
| Relation | All cofinite sets are cocountable | All cofinite sets are cocountable; converse not true |
| Topology Use | Base for cocountable topology | Base for cofinite topology |
| Cardinality of Complement | <= 0 (aleph-null, countably infinite) | Finite (<= n, where n N) |
Introduction to Cocountable and Cofinite Sets
Cocountable and cofinite sets are important concepts in set theory that describe subsets of an infinite set by the nature of their complements. A cocountable set has a complement that is countable, meaning the omitted elements form a set with the same cardinality as the natural numbers or less. In contrast, a cofinite set has a finite complement, implying only finitely many elements are excluded from the whole set, making these definitions useful in topology and real analysis.
Definitions: What is Cocountable?
A set is cocountable if its complement in a given universal set is countable, meaning the rest of the elements outside the set form a countable subset. Cocountable sets often arise in topology, where the cocountable topology includes open sets whose complements are countable or empty. Understanding cocountability helps distinguish between large sets with small complements and their role in various mathematical structures.
Definitions: What is Cofinite?
A set is cofinite if its complement within a given universal set is finite, meaning the set includes all but a finite number of elements from the universal set. In contrast, a set is cocountable if its complement is countable, which could be finite or infinite but countably enumerable. Understanding cofinite sets is crucial in topology and algebra, where they help characterize closed sets and define continuity conditions.
Key Differences Between Cocountable and Cofinite Sets
Cocountable sets are subsets of a given set whose complements are countable, meaning they have a finite or countably infinite number of elements removed from the original set. Cofinite sets specifically have complements that are finite, making the difference that all cofinite sets are cocountable, but not all cocountable sets are cofinite. The key distinction lies in the size of the complement: cocountable sets allow countably infinite complements, while cofinite sets restrict the complement to a strictly finite number of elements.
Examples of Cofinite Sets
Cofinite sets are subsets of a given set whose complements are finite, meaning they contain all elements except a finite number. For example, in the set of natural numbers \(\mathbb{N}\), the set \(\mathbb{N} \setminus \{1, 2, 3\}\) is cofinite because its complement \(\{1, 2, 3\}\) is finite. Another example is the set of all real numbers except a finite number of points, such as \(\mathbb{R} \setminus \{0, 1\}\), which is cofinite since only two points are excluded.
Examples of Cocountable Sets
Cocountable sets are subsets of a set whose complements are countable, such as the real numbers excluding the natural numbers or any uncountable set minus a countable subset like the rationals removed from the reals. For instance, the set of all real numbers except for a finite or countable number of points, like \(\mathbb{R} \setminus \mathbb{Q}\), is cocountable because its complement, the rationals \(\mathbb{Q}\), is countable. Cofinite sets are a specific case where the complement is finite, whereas cocountable sets allow countably infinite complements, illustrating their broader scope in topology and measure theory.
Set Theory Context: Importance of Cocountable and Cofinite
Cocountable sets in set theory are those whose complements are countable, while cofinite sets have complements that are finite. These concepts are crucial in topology and analysis for defining closure properties and convergence criteria within infinite sets. Understanding cocountable and cofinite sets enables mathematicians to characterize important set-theoretic structures and their interactions in infinite contexts.
Relations to Countability and Uncountability
Cocountable sets have complements that are countable, making them relevant in analyzing uncountable spaces by excluding only countably many elements. Cofinite sets have finite complements, thus they relate closely to countability as finite sets are a special case of countable sets. Both concepts illustrate how sets interact with countable or uncountable universes, emphasizing the balance between large sets and their small exceptions.
Applications in Topology and Analysis
Cocountable and cofinite topologies serve significant roles in topology and functional analysis by providing frameworks for convergence and continuity criteria. The cocountable topology, characterized by complements of countable sets as open, aids in studying spaces with dense countable subsets and formulating convergence in spaces lacking usual Euclidean structure. Cofinite topology, defined by complements of finite sets, simplifies compactness arguments and is instrumental in understanding minimal topological conditions for continuity and separation axioms in abstract analysis.
Summary: Choosing Cocountable or Cofinite in Mathematical Proofs
In mathematical proofs, choosing between cocountable and cofinite sets depends on the desired level of strictness regarding the complement's size; cocountable sets have complements with countably infinite elements, while cofinite sets possess finite complements, providing stronger constraints. Cocountable sets are often used in analysis and topology to handle "large" sets within uncountable universes, whereas cofinite sets simplify arguments requiring only finitely many exceptions. Understanding the distinction is crucial for accurately characterizing set properties and ensuring proofs rely on appropriate definitions of largeness or density within infinite sets.
Cocountable Infographic
 libterm.com
libterm.com