Homotopy equivalence is a fundamental concept in algebraic topology that describes when two topological spaces can be continuously deformed into each other, preserving their essential shape. This notion allows mathematicians to classify spaces based on their intrinsic properties rather than their exact geometric form, making it a powerful tool in studying complex structures. Explore the rest of the article to deepen your understanding of homotopy equivalence and its applications.
Table of Comparison
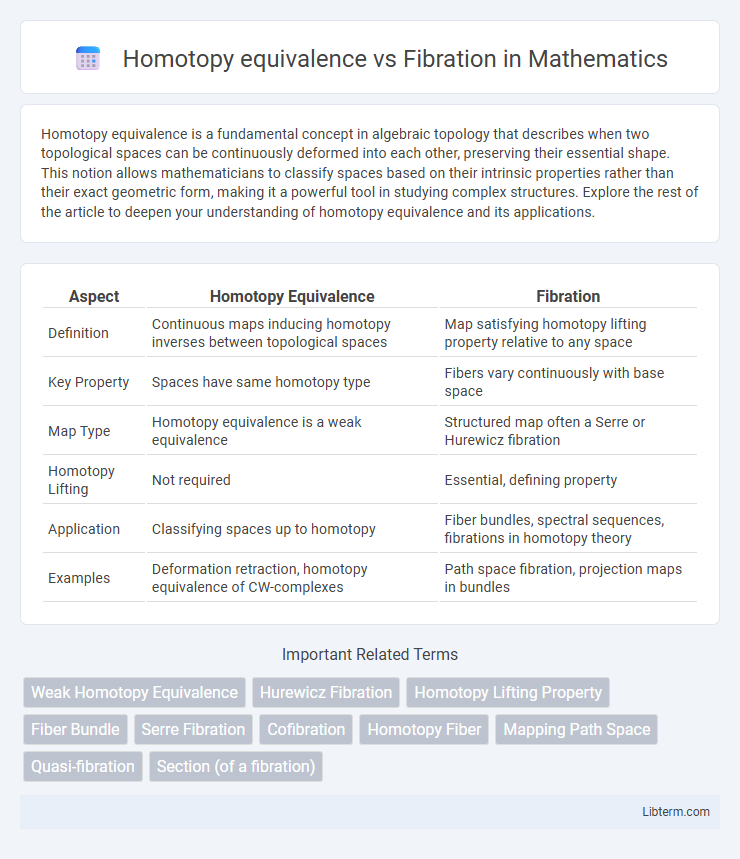
| Aspect | Homotopy Equivalence | Fibration |
|---|---|---|
| Definition | Continuous maps inducing homotopy inverses between topological spaces | Map satisfying homotopy lifting property relative to any space |
| Key Property | Spaces have same homotopy type | Fibers vary continuously with base space |
| Map Type | Homotopy equivalence is a weak equivalence | Structured map often a Serre or Hurewicz fibration |
| Homotopy Lifting | Not required | Essential, defining property |
| Application | Classifying spaces up to homotopy | Fiber bundles, spectral sequences, fibrations in homotopy theory |
| Examples | Deformation retraction, homotopy equivalence of CW-complexes | Path space fibration, projection maps in bundles |
Introduction to Homotopy Equivalence and Fibration
Homotopy equivalence is a fundamental concept in algebraic topology where two spaces are considered equivalent if they can be continuously deformed into each other through homotopy maps. Fibrations are a special class of maps characterized by the homotopy lifting property, essential for studying fiber bundles and their associated long exact sequences. Understanding homotopy equivalence and fibrations lays the foundation for analyzing topological spaces up to deformation and investigating the structure of fiber bundles in homotopy theory.
Fundamental Concepts in Topology
Homotopy equivalence classifies spaces that can be continuously deformed into each other, preserving their essential topological properties. Fibration, characterized by the homotopy lifting property, allows the study of spaces by relating a total space to its base and fiber, facilitating the decomposition of complex topological structures. Understanding these concepts is crucial for analyzing fiber bundles, long exact sequences in homotopy, and the fundamental group actions on covering spaces.
Defining Homotopy Equivalence
Homotopy equivalence is defined by the existence of continuous maps f: X - Y and g: Y - X such that the compositions gf and fg are homotopic to the identity maps on X and Y, respectively. This relation preserves topological properties up to deformation, emphasizing the equivalence of spaces in the homotopy category. Unlike fibrations, which involve a projection map with a homotopy lifting property, homotopy equivalence focuses on the invertibility of maps up to homotopy.
Understanding Fibrations in Topology
Fibrations in topology are maps that satisfy the homotopy lifting property for every space, enabling the study of complex spaces via simpler fiber and base components. Understanding fibrations involves analyzing how continuous maps preserve homotopy equivalence within the fiber structure, ensuring that homotopy types remain consistent between the total space and its fibers. This framework is essential for decomposing spaces in homotopy theory and studying properties like fiber bundles and Serre fibrations.
Core Properties of Homotopy Equivalence
Homotopy equivalence is characterized by the existence of continuous maps between two topological spaces that compose to maps homotopic to the identity, ensuring a strong form of topological similarity. Core properties include invariance of homotopy groups, preservation of homological and cohomological structures, and inducing isomorphisms in all homotopy-invariant functors. Unlike fibrations, which focus on lifting properties and fiber structures, homotopy equivalences guarantee equivalences in global homotopy types.
Essential Features of Fibrations
Fibrations are characterized by the homotopy lifting property, allowing continuous lifting of homotopies from the base space to the total space, which ensures controlled deformation within the fiber structure. Unlike general homotopy equivalences that only guarantee existence of inverse maps up to homotopy, fibrations provide structured fiber bundles with well-defined projection maps preserving fiber homotopy types. Essential features include local triviality, a long exact sequence of homotopy groups, and the ability to model fiberwise homotopy types critical in algebraic topology.
Key Differences between Homotopy Equivalence and Fibration
Homotopy equivalence refers to a continuous map between topological spaces that can be reversed up to homotopy, indicating that the spaces have the same homotopy type. Fibration, specifically a Serre or Hurewicz fibration, involves a continuous surjective map with the homotopy lifting property relative to any space, structuring a fiber bundle-like relationship but not necessarily implying homotopy equivalence of total and base spaces. The key difference lies in their roles: homotopy equivalence characterizes an essential sameness of spaces in homotopy theory, while fibration organizes spaces into fibrations with specified fiber behavior without guaranteeing homotopy equivalence between involved spaces.
Examples Illustrating Homotopy Equivalence
In algebraic topology, examples illustrating homotopy equivalence include the deformation retraction of a solid disk onto its boundary circle, showing the disk and circle share the same homotopy type despite different shapes. The inclusion map from a bouquet of circles into its wedge sum with an additional circle provides another classic example, where this inclusion is a homotopy equivalence due to the contractibility of attaching spaces. These examples contrast with fibrations, where fiber bundles like the Hopf fibration induce homotopy equivalences in fibers but emphasize structural projections rather than direct space equivalences.
Case Studies of Fibrations
Case studies of fibrations reveal that homotopy equivalence plays a crucial role in understanding fiber bundles and their classification spaces. Examples such as the Hopf fibration demonstrate how total spaces, base spaces, and fibers relate through homotopy equivalence to analyze the preservation of topological properties. These case studies highlight the importance of lifting properties and homotopy lifting extensions in establishing fibrations as foundational structures in algebraic topology.
Applications and Significance in Algebraic Topology
Homotopy equivalence serves as a fundamental concept in algebraic topology by classifying spaces up to continuous deformation, thus enabling the simplification of complex topological problems without altering their essential properties. Fibrations provide a structured framework for studying fiber bundles and their homotopy groups, facilitating the analysis of long exact sequences and spectral sequences crucial for computations in homotopy theory. The interplay between homotopy equivalences and fibrations underpins advanced applications such as the construction of classifying spaces, the study of fiber homotopy types, and the development of obstruction theory in topological and geometric contexts.
Homotopy equivalence Infographic
 libterm.com
libterm.com