A circle is a fundamental geometric shape defined by all points equidistant from a central point, known as the center. Its properties include circumference, diameter, radius, and area, which are essential for various mathematical calculations and real-world applications. Discover how understanding the circle can enhance your grasp of geometry and practical problem-solving by reading the rest of this article.
Table of Comparison
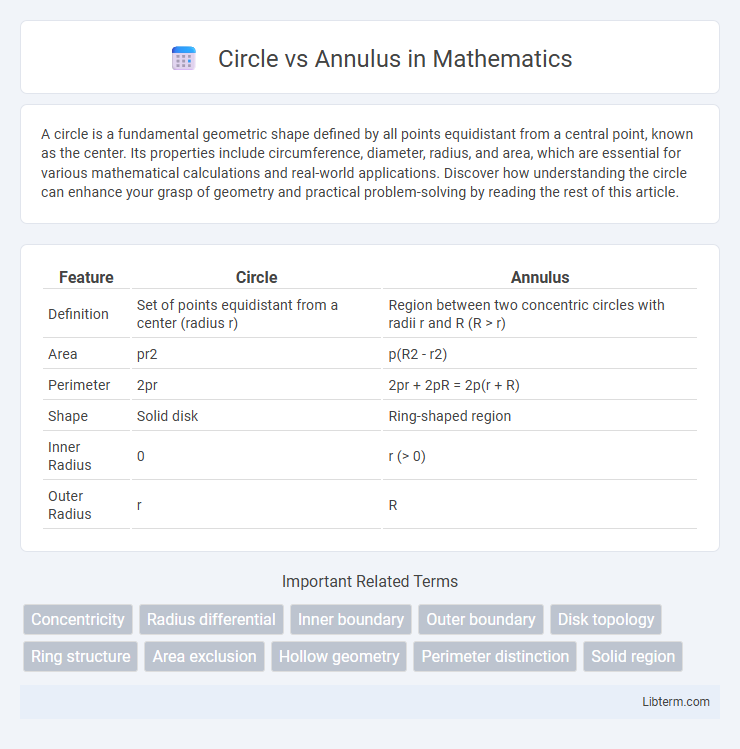
| Feature | Circle | Annulus |
|---|---|---|
| Definition | Set of points equidistant from a center (radius r) | Region between two concentric circles with radii r and R (R > r) |
| Area | pr2 | p(R2 - r2) |
| Perimeter | 2pr | 2pr + 2pR = 2p(r + R) |
| Shape | Solid disk | Ring-shaped region |
| Inner Radius | 0 | r (> 0) |
| Outer Radius | r | R |
Understanding the Basics: Circle and Annulus
A circle is a set of all points in a plane equidistant from a central point, defined by its radius. An annulus is the region between two concentric circles with different radii, representing a ring-shaped area. Understanding these basic properties helps distinguish a solid circular area from a hollow ring-like shape in geometry.
Definition and Key Differences
A circle is a closed curve consisting of all points equidistant from a fixed center point, defined by its radius. An annulus is a ring-shaped region bounded by two concentric circles with different radii, representing the area between them. The key difference lies in the annulus having an inner and outer radius, whereas a circle only has one radius defining its boundary.
Mathematical Properties
A circle is defined as the set of all points equidistant from a fixed center point, characterized by its radius and circumference with the area calculated using the formula pr2. An annulus consists of two concentric circles with different radii, where its area is determined by subtracting the area of the smaller circle from the larger one, given by p(R2 - r2). Both shapes exhibit fundamental properties in Euclidean geometry involving radius, diameter, chord, and central angle measures but differ primarily in spatial region and topology.
Area Formulas: Circle vs. Annulus
The area of a circle is calculated using the formula A = pr2, where r represents the radius of the circle. In contrast, the area of an annulus, which is the region between two concentric circles, is found by subtracting the area of the smaller inner circle from the area of the larger outer circle, expressed as A = p(R2 - r2), where R is the radius of the outer circle and r is the radius of the inner circle. These formulas highlight the key difference in area calculations between a solid circle and the ring-shaped annulus.
Real-Life Applications
A circle, defined by all points equidistant from a center, is fundamental in designing round objects like wheels, clocks, and lenses, where uniform curvature ensures smooth motion and clear focus. An annulus, the region bounded by two concentric circles, appears in engineering applications such as washers, bearings, and pipe cross-sections, where the hollow center allows for weight reduction and fluid flow. Both shapes play crucial roles in mechanical systems, architecture, and manufacturing, optimizing strength, stability, and functional efficiency.
Visual Representation and Diagrams
A circle is visually represented as a single closed curve where all points are equidistant from a central point, typically illustrated with a solid line and a labeled radius from the center to the perimeter. In contrast, an annulus consists of two concentric circles, creating a ring-shaped figure bounded by an inner and outer circle, often depicted with shaded regions to emphasize the area between the two radii. Diagrams of annuli highlight the difference in radii, r (inner radius) and R (outer radius), while circle diagrams focus solely on a single radius and central angle for clarity.
Perimeter and Circumference Comparisons
A circle's perimeter, known as its circumference, is calculated by the formula C = 2pr, where r is the radius. An annulus, formed by two concentric circles with radii r and R (R > r), has a perimeter equal to the sum of the circumferences of both circles, expressed as P = 2pr + 2pR = 2p(r + R). Thus, while a circle's circumference depends on one radius, an annulus' perimeter depends on the sum of the inner and outer radii, representing two boundary lengths.
Common Misconceptions
A common misconception between a circle and an annulus is that both represent two-dimensional shapes with the same area, while in reality, an annulus is a ring-shaped region bounded by two concentric circles with different radii, resulting in an area equal to the difference between the areas of the outer and inner circles. Many confuse the perimeter of the annulus with that of a single circle, but the annulus has two distinct circumferences corresponding to the radii of the inner and outer circles. Understanding the difference in these geometric properties is essential for correctly applying formulas in problems involving circular regions.
Importance in Geometry and Engineering
The circle, defined by all points equidistant from a center, serves as a fundamental shape in geometry crucial for understanding concepts like symmetry, area, and circumference. The annulus, a ring-shaped region bounded by two concentric circles, plays a significant role in engineering by modeling components such as bearings and pipe cross-sections, where material properties and structural integrity depend on annular measurements. Precise calculations involving circles and annuli enable optimization of mechanical designs and ensure efficient material usage in various engineering applications.
Summary Table: Circle vs. Annulus
The summary table for Circle vs. Annulus highlights that a circle is a closed curve representing all points equidistant from a center, characterized by radius, diameter, and area formulas pr2 and pd2/4. An annulus is the region bounded between two concentric circles with different radii, defined by inner radius r and outer radius R, with the area calculated as p(R2 - r2). Key differences include the circle's single radius and uniform curvature versus the annulus's dual radii and ring-like shape.
Circle Infographic
 libterm.com
libterm.com