Differentiable functions allow you to compute derivatives, which are essential for understanding rates of change in various mathematical and real-world contexts. These functions must be smooth and continuous, enabling precise calculations in calculus and optimization problems. Explore the rest of this article to deepen your understanding of differentiability and its significance in advanced mathematics.
Table of Comparison
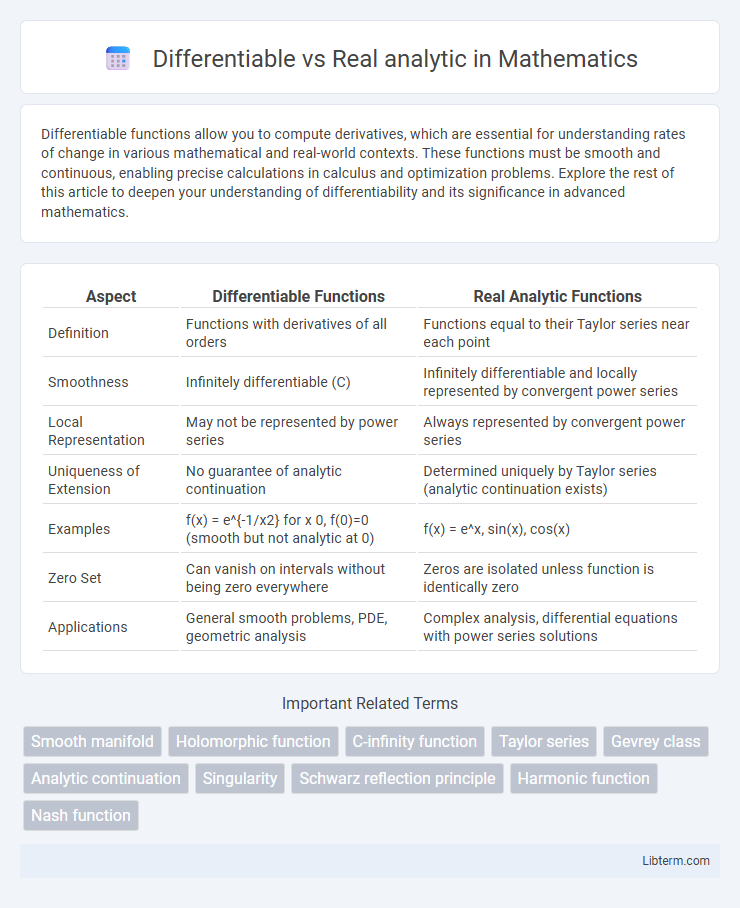
| Aspect | Differentiable Functions | Real Analytic Functions |
|---|---|---|
| Definition | Functions with derivatives of all orders | Functions equal to their Taylor series near each point |
| Smoothness | Infinitely differentiable (C) | Infinitely differentiable and locally represented by convergent power series |
| Local Representation | May not be represented by power series | Always represented by convergent power series |
| Uniqueness of Extension | No guarantee of analytic continuation | Determined uniquely by Taylor series (analytic continuation exists) |
| Examples | f(x) = e^{-1/x2} for x 0, f(0)=0 (smooth but not analytic at 0) | f(x) = e^x, sin(x), cos(x) |
| Zero Set | Can vanish on intervals without being zero everywhere | Zeros are isolated unless function is identically zero |
| Applications | General smooth problems, PDE, geometric analysis | Complex analysis, differential equations with power series solutions |
Introduction to Differentiable and Real Analytic Functions
Differentiable functions are those that possess derivatives at each point within their domain, enabling the use of calculus techniques for local linear approximations. Real analytic functions are a subclass characterized by being representable as convergent power series around every point in their domain, ensuring infinite differentiability and stronger structural properties. Understanding the distinction between these functions is crucial for fields like differential geometry and complex analysis, where the nature of smoothness impacts solution behavior and function classification.
Core Definitions: Differentiability vs Real Analyticity
Differentiability refers to a function having a well-defined derivative at a point, meaning it can be locally approximated by a linear map. Real analyticity requires a function to be expressible as a convergent power series around a point, ensuring infinite differentiability and a stronger form of local approximability. While all real analytic functions are infinitely differentiable, not all differentiable functions are real analytic.
Key Mathematical Distinctions
Differentiable functions are defined by the existence of derivatives at each point within their domain, allowing local linear approximations, while real analytic functions require their Taylor series to converge exactly to the function in a neighborhood around every point. The key mathematical distinction lies in real analytic functions being infinitely differentiable with representatives by power series, contrasting with merely differentiable functions where derivatives may exist without guaranteeing such series expansions. Analyticity implies strong rigidity and structural properties, whereas differentiability alone permits more flexible, less constrained function behavior.
Examples of Differentiable but Not Analytic Functions
A classic example of a function that is differentiable everywhere but not analytic is \( f(x) = e^{-1/x^2} \) for \( x \neq 0 \) and \( f(0) = 0 \), which is infinitely differentiable but has a Taylor series at zero that converges only to zero, not to the function itself. Smooth bump functions, used in differential geometry and functional analysis, provide other cases where functions have derivatives of all orders but fail to be expressible as convergent power series near certain points. These examples illustrate the distinction between differentiability--a requirement of smoothness--and real analyticity, which demands local expressibility via converging power series.
Real Analytic Functions: Properties and Applications
Real analytic functions are distinguished by their ability to be locally represented by a convergent power series, ensuring infinite differentiability and strong uniqueness properties. These functions exhibit exceptional smoothness and rigidity, allowing precise approximations and predictions in complex analysis, differential equations, and dynamical systems. Applications span from solving boundary value problems to modeling physical phenomena where exact behavior near points is crucial, highlighting their significance over merely differentiable functions.
When Differentiability Implies Analyticity
When a function is differentiable in the complex plane (holomorphic) on an open set, it is automatically real analytic, meaning it can be locally represented by a convergent power series. Real differentiability in the real domain does not necessarily imply analyticity, but complex differentiability imposes stronger conditions that ensure analyticity. Functions satisfying the Cauchy-Riemann equations have derivatives of all orders, guaranteeing real analyticity on open subsets of the complex plane.
Importance in Calculus and Analysis
Differentiable functions are crucial in calculus as they guarantee the existence of derivatives, enabling the study of rates of change and local linear approximations. Real analytic functions, which are infinitely differentiable and equal to their Taylor series expansions within a radius of convergence, play a fundamental role in analysis by allowing precise function reconstruction and facilitating deep insights into function behavior. Understanding the distinction between general differentiability and real analyticity is essential for advanced problem-solving in differential equations, complex analysis, and mathematical modeling.
The Role in Differential Equations
Differentiable functions provide the basic framework for solving differential equations by allowing local linear approximations and the application of derivative operations. Real analytic functions, characterized by convergent power series expansions, offer stronger conditions that guarantee uniqueness and extend solutions beyond local neighborhoods through analytic continuation. These properties make real analytic functions crucial in ensuring global behavior and stability in the solutions of many differential equations.
Practical Considerations in Mathematical Modeling
Differentiable functions, characterized by the existence of derivatives at every point, offer flexibility and ease of use in numerical methods and simulations, making them practical for modeling real-world phenomena with potential irregularities. Real analytic functions, defined by convergent power series expansions in neighborhoods, provide stronger structural properties that guarantee predictability and stability in models but require stricter smoothness assumptions. Choosing between differentiable and real analytic frameworks depends on the desired balance between computational tractability and the precision of analytic continuation in mathematical modeling.
Conclusion: Choosing Between Differentiable and Real Analytic
Choosing between differentiable and real analytic functions depends on the desired properties and applications: differentiable functions allow flexibility and broader applicability, while real analytic functions ensure stronger convergence and unique power series representation. In contexts requiring precise behavior modeling and strong constraints, real analytic functions are preferred. For general purposes where smoothness suffices without stringent structural requirements, differentiable functions offer a suitable framework.
Differentiable Infographic
 libterm.com
libterm.com