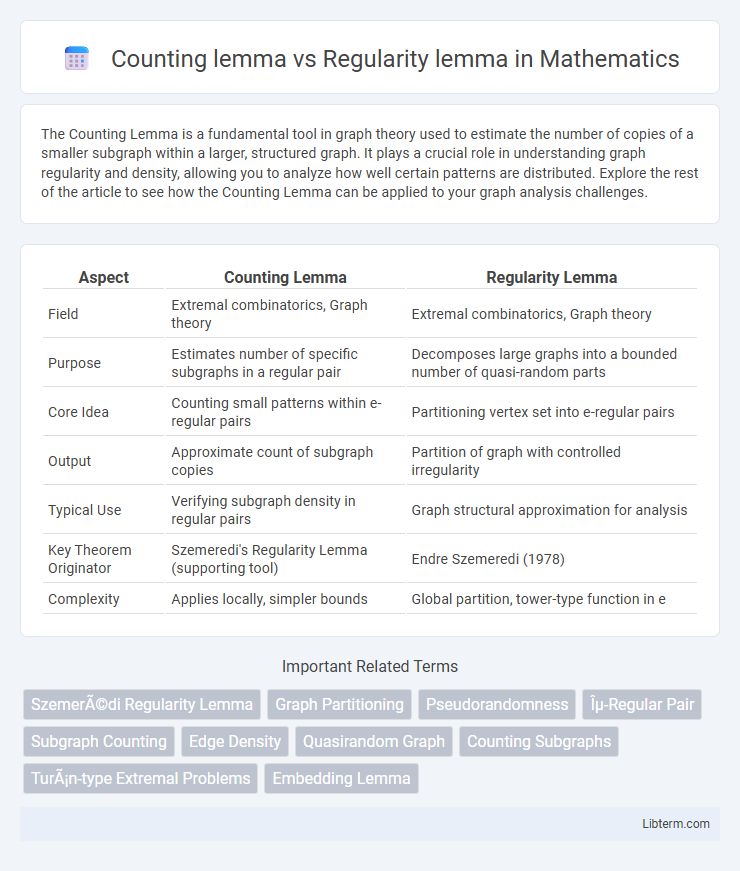
The Counting Lemma is a fundamental tool in graph theory used to estimate the number of copies of a smaller subgraph within a larger, structured graph. It plays a crucial role in understanding graph regularity and density, allowing you to analyze how well certain patterns are distributed. Explore the rest of the article to see how the Counting Lemma can be applied to your graph analysis challenges.
Table of Comparison
| Aspect | Counting Lemma | Regularity Lemma |
|---|---|---|
| Field | Extremal combinatorics, Graph theory | Extremal combinatorics, Graph theory |
| Purpose | Estimates number of specific subgraphs in a regular pair | Decomposes large graphs into a bounded number of quasi-random parts |
| Core Idea | Counting small patterns within e-regular pairs | Partitioning vertex set into e-regular pairs |
| Output | Approximate count of subgraph copies | Partition of graph with controlled irregularity |
| Typical Use | Verifying subgraph density in regular pairs | Graph structural approximation for analysis |
| Key Theorem Originator | Szemeredi's Regularity Lemma (supporting tool) | Endre Szemeredi (1978) |
| Complexity | Applies locally, simpler bounds | Global partition, tower-type function in e |
Introduction to Graph Theory Lemmas
The Counting Lemma and Regularity Lemma are fundamental tools in graph theory, particularly in the study of dense graphs. The Regularity Lemma, introduced by Szemeredi, partitions large graphs into a bounded number of random-like bipartite subgraphs, enabling complex structure analysis. The Counting Lemma complements it by providing precise estimates for the number of small subgraphs within these pseudorandom partitions, crucial for embedding patterns and subgraph counting.
What is the Regularity Lemma?
The Regularity Lemma, formulated by Endre Szemeredi, is a fundamental tool in graph theory and combinatorics that approximates any large graph by a union of a bounded number of random-like bipartite graphs called regular pairs. This lemma states that for every e > 0, any sufficiently large graph can be partitioned into a finite number of vertex subsets such that most pairs of subsets exhibit e-regularity, meaning their edge distribution is uniformly random-like. Its applications range from graph property testing to proving deep results in additive number theory and theoretical computer science.
What is the Counting Lemma?
The Counting Lemma is a fundamental combinatorial result that estimates the number of copies of a small fixed graph within a large, dense, and suitably pseudorandom host graph. It provides precise quantitative bounds when the host graph meets certain regularity conditions, allowing accurate counting of subgraph occurrences. This lemma plays a crucial role in graph theory by bridging the structural insights given by the Regularity Lemma with explicit enumerative consequences.
Key Differences Between Counting and Regularity Lemmas
The Counting lemma provides precise estimates for the number of small subgraphs within a larger graph based on a given partition, relying on quasirandomness conditions. In contrast, the Regularity lemma offers a way to partition any large graph into a bounded number of random-like regular pairs, facilitating structural analysis but without directly counting subgraphs. The key difference lies in the Counting lemma's quantitative focus on subgraph frequencies versus the Regularity lemma's qualitative structural decomposition of graphs.
Applications of the Regularity Lemma
The Regularity Lemma is pivotal in graph theory and combinatorics, enabling the approximation of large graphs by structured, random-like partitions, which aids in solving problems related to graph property testing, embedding large graphs, and proving graph removal lemmas. Its applications extend to number theory and computer science, particularly in designing efficient algorithms for dense graph property testing and in combinatorial optimization. Compared to the Counting Lemma, the Regularity Lemma provides a broader framework for analyzing complex graph structures despite offering less precise edge counts.
Applications of the Counting Lemma
The Counting Lemma plays a crucial role in combinatorics by providing precise estimates for the number of copies of a fixed subgraph within regular pairs, enabling accurate density calculations in graph structures. This lemma is essential in applying the Szemeredi Regularity Lemma, where it bridges the gap between approximate regular partitions and exact subgraph counts, facilitating proofs in extremal graph theory and additive number theory. Its applications extend to property testing, algorithmic graph theory, and proving the removal lemmas essential for understanding large combinatorial configurations.
How the Regularity Lemma Supports the Counting Lemma
The Regularity Lemma decomposes large graphs into a bounded number of random-like bipartite subgraphs, enabling a structured approximation of complex graph behavior. This decomposition creates uniform pairs, which the Counting Lemma leverages to accurately estimate the number of small subgraphs within the larger graph. By ensuring these pairs behave pseudorandomly, the Regularity Lemma provides the necessary framework for the Counting Lemma to perform precise subgraph counting, critical for applications in extremal graph theory and combinatorics.
Limitations and Challenges of Each Lemma
The Counting Lemma faces challenges in handling sparse graphs, as its accuracy diminishes when edge densities become too low or irregular, limiting its applicability in certain combinatorial structures. The Regularity Lemma, while powerful for decomposing large graphs into regular pairs, suffers from massive tower-type bounds on the size of the partitions, making it computationally infeasible for practical use in large-scale problems. Both lemmas struggle with balancing precision and complexity, where Counting Lemma requires strong regularity conditions and Regularity Lemma incurs severe combinatorial explosion in partition sizes, hindering their direct computational implementation.
Practical Examples in Extremal Graph Theory
The Counting Lemma provides precise estimates for the number of small subgraphs within a larger regular pair, proving essential in analyzing triangles and cliques during extremal graph problems. The Regularity Lemma, by partitioning large graphs into a bounded number of e-regular pairs, simplifies complex network structures to facilitate these counting arguments. Practical applications include bounding Turan numbers and detecting forbidden subgraphs by combining both lemmas to approximate the frequency of patterns in dense graphs.
Summary: Comparing Counting Lemma vs Regularity Lemma
The Counting Lemma provides precise estimates for the number of specific subgraphs within a structured graph, relying on e-regular pairs to guarantee these counts. The Regularity Lemma, in contrast, partitions any large graph into a bounded number of e-regular pairs, offering a global approximation of the graph's structure. Together, the Regularity Lemma sets up the partition framework, while the Counting Lemma enables exact subgraph enumeration within those partitions.
Counting lemma Infographic
 libterm.com
libterm.com