The pullback functor plays a crucial role in category theory and algebraic geometry by allowing the transfer of structures along morphisms. It provides a systematic way to "pull back" sheaves, bundles, or objects from one space to another, preserving essential properties. Explore this article to understand how the pullback functor operates and why it is vital for your studies in advanced mathematics.
Table of Comparison
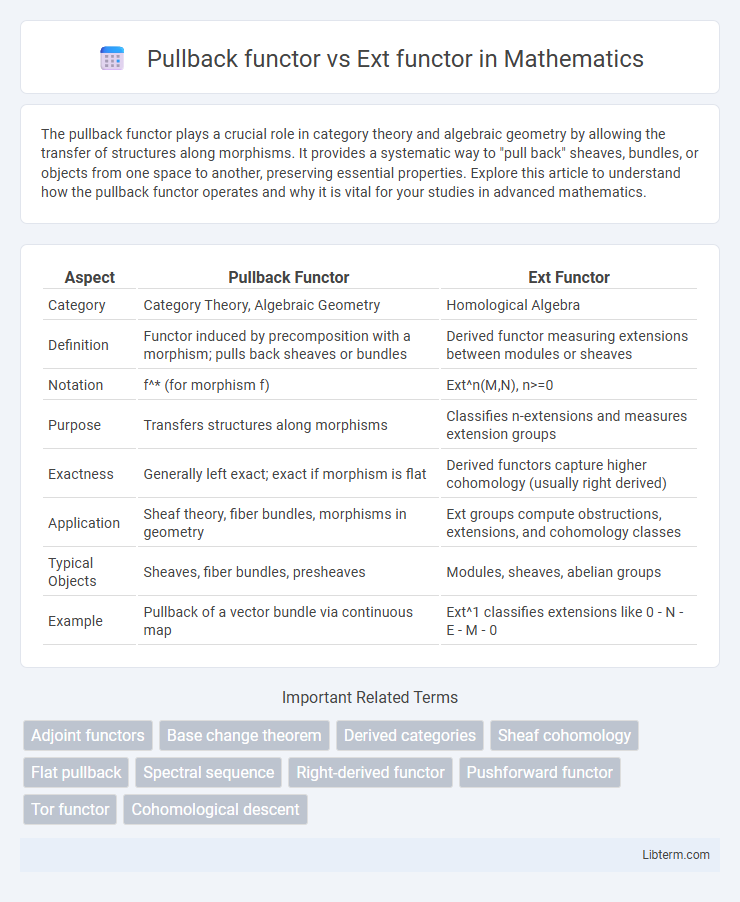
| Aspect | Pullback Functor | Ext Functor |
|---|---|---|
| Category | Category Theory, Algebraic Geometry | Homological Algebra |
| Definition | Functor induced by precomposition with a morphism; pulls back sheaves or bundles | Derived functor measuring extensions between modules or sheaves |
| Notation | f^* (for morphism f) | Ext^n(M,N), n>=0 |
| Purpose | Transfers structures along morphisms | Classifies n-extensions and measures extension groups |
| Exactness | Generally left exact; exact if morphism is flat | Derived functors capture higher cohomology (usually right derived) |
| Application | Sheaf theory, fiber bundles, morphisms in geometry | Ext groups compute obstructions, extensions, and cohomology classes |
| Typical Objects | Sheaves, fiber bundles, presheaves | Modules, sheaves, abelian groups |
| Example | Pullback of a vector bundle via continuous map | Ext^1 classifies extensions like 0 - N - E - M - 0 |
Introduction to Functors in Category Theory
The pullback functor in category theory maps objects and morphisms along a given morphism, preserving the structure of fibered categories. The Ext functor, derived from homological algebra, measures extensions between objects, capturing higher-dimensional morphisms in abelian categories. Both functors illustrate how categorical constructions encode algebraic and geometric properties through functorial relationships.
Overview of Pullback Functor
The pullback functor, often denoted as \( f^* \), maps objects and morphisms in a category along a fixed morphism \( f: X \to Y \), preserving the structure through inverse image constructions. It plays a crucial role in sheaf theory and algebraic geometry by transferring sheaves or modules from the target space \( Y \) to the source space \( X \), enabling comparison and analysis of local data. Unlike the Ext functor, which measures extensions and derived functor cohomology, the pullback functor is exact in many contexts and serves as a foundational tool for constructing fibered categories and analyzing base change phenomena.
Overview of Ext Functor
The Ext functor, denoted as Ext^n, measures extensions of modules and classifies n-extensions between them, playing a central role in homological algebra. It arises as the right derived functor of the Hom functor, capturing information about the failure of exactness when applying Hom to a short exact sequence. Ext groups provide crucial invariants in module theory, representation theory, and algebraic geometry, enabling the study of extensions, obstructions, and cohomology classes.
Categorical Foundations: Pullbacks and Extensions
Pullback functors arise from pullback squares in category theory, enabling the reindexing of objects along morphisms and preserving limits such as finite limits. Ext functors, originating in homological algebra, measure extensions of modules or objects in abelian categories, capturing higher-dimensional extension classes via derived functors of Hom. Categorical foundations link pullbacks to limit constructions, while Ext functors relate to derived categories and cohomological methods, highlighting their complementary roles in analyzing structures and morphisms in categories.
Formal Definitions and Notations
The pullback functor, often denoted as \( f^* \) for a morphism \( f: X \to Y \), maps sheaves or modules from the target category over \( Y \) to the source category over \( X \), preserving the inverse image structure. The Ext functor, \( \mathrm{Ext}^n_R(M, N) \), defined in homological algebra, measures extensions of modules \( M \) and \( N \) over a ring \( R \), computed as the right derived functors of \( \mathrm{Hom}_R(M, -) \). While the pullback functor acts on objects via precomposition with \( f \), the Ext functor captures higher cohomological information about module extensions, emphasizing their distinct categorical and homological roles.
Pullback Functor in Sheaf Theory
The pullback functor in sheaf theory, denoted as \( f^* \), assigns to each sheaf on a topological space \( Y \) a sheaf on \( X \) via a continuous map \( f: X \to Y \), preserving the local structure by pulling back sections along \( f \). Unlike the Ext functor, which measures extensions and homological dimensions between sheaves, the pullback functor is exact on sheaves of sets and right exact on abelian sheaves, crucial for defining inverse image sheaves and for computations in derived categories. This functor plays a fundamental role in sheaf cohomology, algebraic geometry, and the study of fibered spaces, enabling transfer of complex geometric and topological data between spaces.
Ext Functor in Homological Algebra
Ext functor in homological algebra measures extensions of modules, providing a derived functor of Hom that captures obstructions to lifting module homomorphisms. It plays a critical role in classifying extensions and computing cohomology groups, essential for understanding module structure and extensions. Unlike the pullback functor, which pulls back objects along morphisms, Ext functors extract higher-level extension information crucial for derived category theory and homological computations.
Key Differences Between Pullback and Ext Functors
Pullback functors are induced by a morphism between topological spaces or schemes, translating sheaves or modules along that map, primarily preserving structure by "pulling back" objects. Ext functors, arising from homological algebra, measure extensions and classify equivalence classes of exact sequences, providing deeper information about module or sheaf cohomology. The key difference lies in the pullback functor's role in geometric transformation and the Ext functor's role in capturing extension and cohomological properties of algebraic objects.
Applications in Algebraic Geometry and Topology
The pullback functor, crucial in algebraic geometry, enables the transfer of sheaves along morphisms, preserving geometric structures and facilitating fiber product computations. The Ext functor, prominent in both algebraic geometry and topology, measures extensions and obstructions in module and sheaf categories, playing a key role in deformation theory and spectral sequence analysis. Their interplay is essential for understanding cohomological phenomena, such as sheaf cohomology and derived categories, which underpin modern approaches to moduli problems and duality theories.
Comparative Summary and Further Reading
The Pullback functor preserves limits and is right adjoint to the pushforward functor, playing a crucial role in fibered categories and sheaf theory, whereas the Ext functor measures extensions of modules and serves as a derived functor of Hom in homological algebra. Pullback functors are exact and maintain structural properties in categorical frameworks, while Ext functors are generally left derived and provide insight into dimension and cohomology theories. For deeper understanding, consult Mac Lane's "Categories for the Working Mathematician" for pullbacks and Weibel's "An Introduction to Homological Algebra" for Ext functors.
Pullback functor Infographic
 libterm.com
libterm.com