The tensor product is a fundamental operation in linear algebra that combines two vector spaces into a new, higher-dimensional space, capturing interactions between vectors. This concept plays a crucial role in quantum mechanics, computer graphics, and multilinear algebra by enabling the representation of complex systems. Explore the rest of the article to understand how tensor products enhance your mathematical toolkit and their practical applications.
Table of Comparison
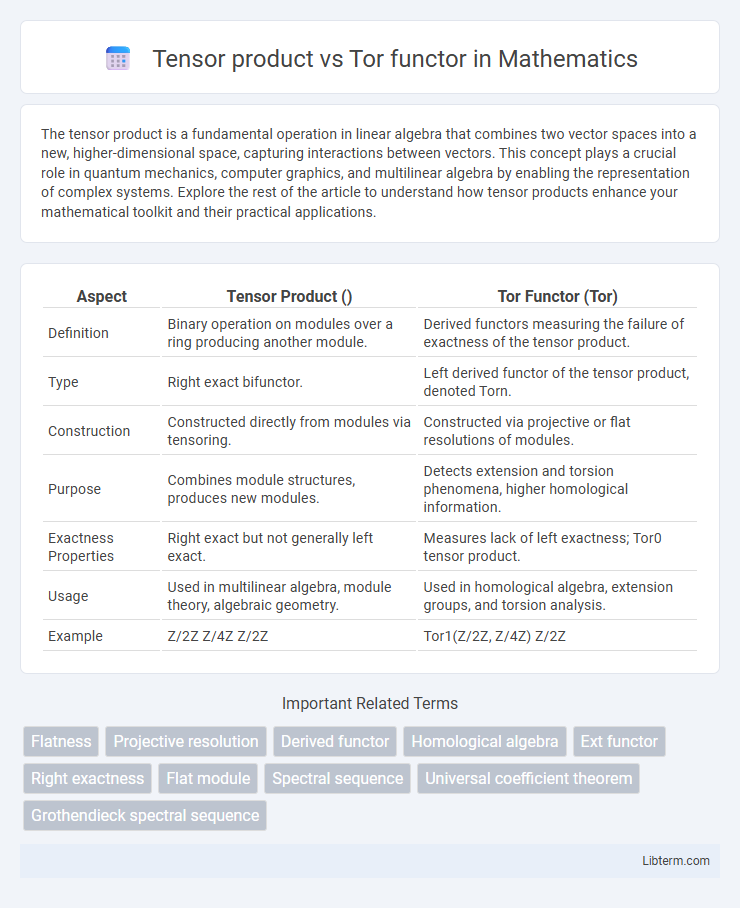
| Aspect | Tensor Product () | Tor Functor (Tor) |
|---|---|---|
| Definition | Binary operation on modules over a ring producing another module. | Derived functors measuring the failure of exactness of the tensor product. |
| Type | Right exact bifunctor. | Left derived functor of the tensor product, denoted Torn. |
| Construction | Constructed directly from modules via tensoring. | Constructed via projective or flat resolutions of modules. |
| Purpose | Combines module structures, produces new modules. | Detects extension and torsion phenomena, higher homological information. |
| Exactness Properties | Right exact but not generally left exact. | Measures lack of left exactness; Tor0 tensor product. |
| Usage | Used in multilinear algebra, module theory, algebraic geometry. | Used in homological algebra, extension groups, and torsion analysis. |
| Example | Z/2Z Z/4Z Z/2Z | Tor1(Z/2Z, Z/4Z) Z/2Z |
Introduction to Tensor Product and Tor Functor
The tensor product of modules over a ring provides a way to construct a new module that encodes bilinear maps, playing a fundamental role in homological algebra and module theory. The Tor functor arises as a derived functor of the tensor product, measuring the extent to which the tensor product fails to be exact, thus capturing torsion-related information in module extensions. Understanding the tensor product and Tor functor is essential for analyzing projective resolutions, computing homology groups, and exploring the structure of modules over rings.
Algebraic Background: Modules and Exact Sequences
The tensor product of modules over a ring measures how modules combine, preserving exactness in sequences where modules are flat, while the Tor functor arises as the left derived functor of the tensor product, capturing information about the failure of exactness when tensoring with non-flat modules. In the context of exact sequences, the tensor product is right exact but not necessarily left exact, making Tor groups essential for detecting extensions and torsion phenomena in homological algebra. Modules, projective resolutions, and exact sequences form the algebraic framework where the interplay between tensor products and Tor functors reveals deeper structural properties of objects in module categories.
Defining the Tensor Product: Basics and Properties
The tensor product of two modules over a commutative ring R, denoted \(M \otimes_R N\), constructs a new module capturing bilinear maps from the Cartesian product \(M \times N\). It is defined by the universal property that any bilinear map factors uniquely through the tensor product, ensuring its uniqueness up to isomorphism. Key properties include right exactness and the ability to distribute over direct sums, making the tensor product foundational for studying module extensions and homological algebra.
Understanding the Tor Functor: Motivation and Definition
The Tor functor arises in homological algebra as a tool to measure the failure of the tensor product to be exact, capturing torsion phenomena in modules over a ring. It is defined via projective resolutions, where applying the tensor product to a projective resolution of one module and taking homology yields the derived functors Tor_n, which quantify extensions and obstructions beyond the tensor product. Understanding the Tor functor involves recognizing its role in detecting hidden relationships between modules that the tensor product alone cannot reveal, especially in contexts involving non-flat modules.
Key Differences Between Tensor Product and Tor Functor
Tensor product, denoted by , is a bifunctor used to construct a new module from two modules over a commutative ring, preserving exact sequences only in the right argument but not in the left. Tor functor, denoted by Tor_i^R(-,-), is a derived functor of the tensor product that measures the failure of the tensor product to be exact, capturing higher homological information such as extension and torsion phenomena. Key differences include the fact that the tensor product is a right-exact functor producing modules, whereas the Tor functor is a family of left derived functors providing homological invariants in multiple degrees.
Homological Perspective: Projective Resolutions and Derived Functors
The tensor product is a right exact functor that measures the interaction between modules, while the Tor functor arises as its left derived functor, capturing the failure of exactness. Projective resolutions are used to compute Tor groups by resolving modules into projective modules, allowing the application of the tensor product functor to derive homological invariants. This homological perspective through derived functors reveals deeper structural information about extensions and relations between modules beyond direct tensoring.
Examples Illustrating Tensor Product vs Tor Functor
The tensor product of modules, such as \(\mathbb{Z}/2\mathbb{Z} \otimes_{\mathbb{Z}} \mathbb{Z}/4\mathbb{Z} \cong \mathbb{Z}/2\mathbb{Z}\), demonstrates how it combines modules but may overlook torsion phenomena. The Tor functor, especially \(\mathrm{Tor}_1^{\mathbb{Z}}(\mathbb{Z}/2\mathbb{Z}, \mathbb{Z}/4\mathbb{Z}) \cong \mathbb{Z}/2\mathbb{Z}\), detects torsion elements that tensor products miss, revealing extension and interaction properties. These examples highlight that Tor functors capture homological information related to projective resolutions and torsion, which the tensor product alone cannot reflect.
Applications in Algebra and Topology
The tensor product is fundamental in algebra for constructing new modules and rings by combining existing structures, allowing the study of bilinear maps and extension of scalars, while the Tor functor measures the failure of exactness in tensoring, detecting torsion phenomena and providing crucial invariants in homological algebra. In topology, the tensor product helps compute homology groups of product spaces, whereas the Tor functor arises in spectral sequences and universal coefficient theorems, linking homology and cohomology with coefficients in different modules. Both tools are essential in classifying complex algebraic and topological structures through their ability to capture finer module interactions and obstruction classes.
Computing Tor: Methods and Tools
Computing Tor functors involves using projective resolutions and chain complexes to measure the failure of exactness in tensor products, providing insights into derived functors in homological algebra. Tools such as spectral sequences, computer algebra systems like Macaulay2 and SageMath, and software libraries specializing in homological computations facilitate the calculation of Tor groups explicitly. These methods enable the effective handling of complex algebraic structures, such as modules over rings, by algorithmically resolving tensor product limitations through homological methods.
Summary and Further Reading on Tensor Product and Tor Functor
The tensor product combines two modules over a ring into a new module, capturing bilinear relations, while the Tor functor measures the failure of exactness in tensoring, providing crucial homological information about module extensions and flatness. Key properties include the right exactness of the tensor product and the derived nature of Tor functors, which arise from projective resolutions in homological algebra. For further reading, explore classic texts like "An Introduction to Homological Algebra" by Charles A. Weibel and "Homological Algebra" by Henri Cartan and Samuel Eilenberg, which offer in-depth treatments of these fundamental constructions.
Tensor product Infographic
 libterm.com
libterm.com