Finsler geometry extends classical Riemannian geometry by generalizing the notion of distance through a norm that varies smoothly with position and direction, enabling the study of more complex spaces. This framework plays a crucial role in various fields such as physics, optimization, and control theory due to its flexibility in handling anisotropic environments. Explore the rest of this article to deepen your understanding of Finsler geometry and its diverse applications.
Table of Comparison
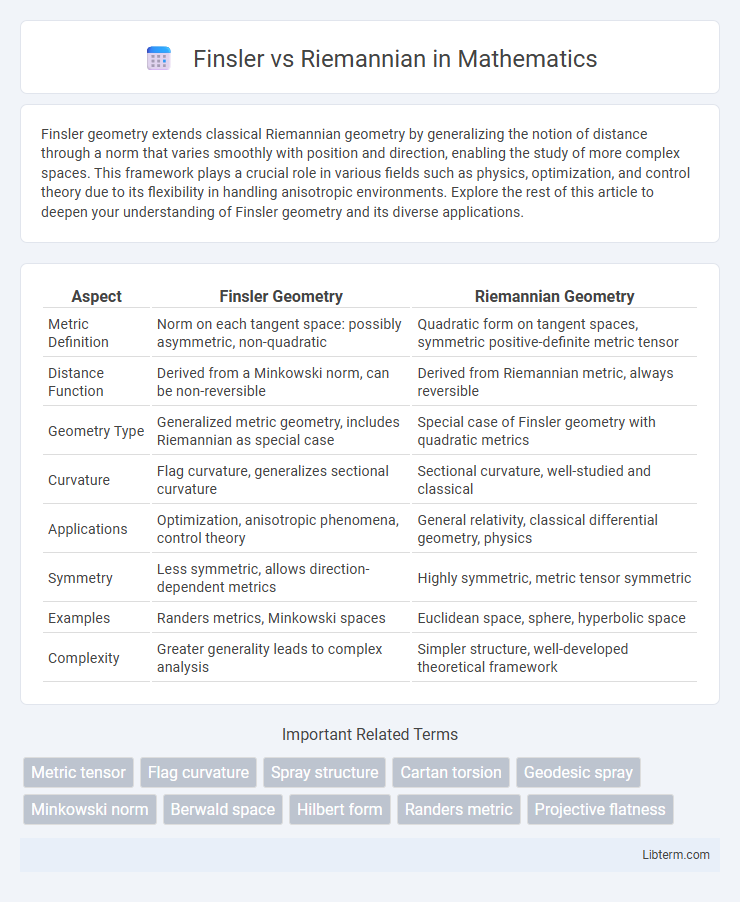
| Aspect | Finsler Geometry | Riemannian Geometry |
|---|---|---|
| Metric Definition | Norm on each tangent space: possibly asymmetric, non-quadratic | Quadratic form on tangent spaces, symmetric positive-definite metric tensor |
| Distance Function | Derived from a Minkowski norm, can be non-reversible | Derived from Riemannian metric, always reversible |
| Geometry Type | Generalized metric geometry, includes Riemannian as special case | Special case of Finsler geometry with quadratic metrics |
| Curvature | Flag curvature, generalizes sectional curvature | Sectional curvature, well-studied and classical |
| Applications | Optimization, anisotropic phenomena, control theory | General relativity, classical differential geometry, physics |
| Symmetry | Less symmetric, allows direction-dependent metrics | Highly symmetric, metric tensor symmetric |
| Examples | Randers metrics, Minkowski spaces | Euclidean space, sphere, hyperbolic space |
| Complexity | Greater generality leads to complex analysis | Simpler structure, well-developed theoretical framework |
Introduction to Finsler and Riemannian Geometry
Finsler geometry generalizes Riemannian geometry by allowing the metric to be a norm that varies smoothly on the tangent bundle, rather than a quadratic form. Riemannian geometry studies smooth manifolds equipped with a positive-definite metric tensor defining infinitesimal distances through an inner product. This fundamental difference leads Finsler geometry to describe more general metric spaces with applications in physics and optimization that extend beyond the classical Riemannian framework.
Fundamental Definitions and Concepts
Finsler geometry generalizes Riemannian geometry by allowing the metric to depend on both position and direction, defining a norm on each tangent space rather than an inner product. The fundamental object in Riemannian geometry is the metric tensor \(g_{ij}\), a smoothly varying positive-definite inner product on tangent spaces, whereas Finsler geometry replaces this with a Finsler function \(F(x, y)\) that is positive, positively homogeneous, and smooth on the slit tangent bundle. This leads to distinct notions of length and curvature, where Riemannian length is computed via quadratic forms and Finsler length arises from more general Minkowski norms, enabling the study of more flexible and anisotropic geometries.
Historical Development and Key Mathematicians
Finsler geometry, introduced by Paul Finsler in 1918, extends Riemannian geometry by allowing the metric to be non-quadratic, thereby generalizing distance measurement in manifolds. Bernhard Riemann laid the foundational framework in the 19th century with his 1854 lecture on the foundations of geometry, introducing Riemannian metrics based on quadratic forms. Subsequent key mathematicians like Elie Cartan and Hermann Weyl further developed differential geometry, helping to establish the formal properties and applications of both Finsler and Riemannian structures.
Core Differences Between Finsler and Riemannian Metrics
Finsler metrics generalize Riemannian metrics by allowing the norm on each tangent space to be non-quadratic and potentially asymmetric, while Riemannian metrics require a positive-definite quadratic form. The core difference lies in Finsler geometry's flexibility to define distance functions using Minkowski norms, contrasting with Riemannian geometry's strict reliance on inner products to measure lengths and angles. Consequently, geodesics and curvature properties differ significantly, with Finsler metrics accommodating anisotropic and direction-dependent behaviors not present in Riemannian structures.
Geodesics in Finsler and Riemannian Spaces
Geodesics in Riemannian spaces are curves that locally minimize distance based on a metric defined by an inner product on tangent spaces, resulting in well-behaved and symmetric distance functions. In contrast, geodesics in Finsler spaces arise from a norm on tangent spaces, which may lack quadratic structure, leading to potentially asymmetric and more general distance measures. The study of geodesics in Finsler geometry involves analyzing the variation of the Finsler norm and leads to nonlinear differential equations, extending the classical Riemannian geodesic equations.
Curvature: Comparing Finsler and Riemannian Approaches
Finsler geometry extends Riemannian concepts by allowing the metric to depend non-quadratically on tangent vectors, resulting in curvature measures that generalize sectional curvature into flag curvature. While Riemannian curvature tensors derive from symmetric positive-definite metrics yielding isotropic behavior, Finsler curvature exhibits anisotropy reflecting directional dependence. This leads to richer geometric structures in Finsler spaces, with applications in differential geometry and physics where non-Euclidean anisotropic metrics are essential.
Applications in Physics and Engineering
Finsler geometry generalizes Riemannian geometry by allowing the metric to depend on both position and direction, which enhances modeling capabilities in physics and engineering fields such as anisotropic materials and complex fluid dynamics. Unlike Riemannian metrics, Finsler metrics capture directional dependencies crucial for analyzing wave propagation in anisotropic media and optimizing trajectories in robotics and control systems. This flexibility makes Finsler geometry particularly valuable in general relativity extensions and the design of advanced materials with direction-dependent properties.
Advantages and Limitations of Each Geometry
Finsler geometry generalizes Riemannian geometry by allowing the metric to be non-quadratic, offering greater flexibility in modeling anisotropic spaces and handling more complex distance measures. Riemannian geometry benefits from a well-established theoretical framework and simpler computational techniques due to its quadratic metric form, making it suitable for many classical applications in physics and engineering. However, Finsler geometry's complexity can lead to challenging calculations and less-developed tools, while Riemannian geometry may be limited in capturing phenomena involving direction-dependent metrics or irregular geometries.
Recent Research and Developments
Recent research in Finsler geometry emphasizes its applications in general relativity, where anisotropic spacetime models extend classical Riemannian frameworks. Advances in metric geometry highlight Finsler spaces' role in optimal transport and variational problems, surpassing Riemannian structural constraints. Computational techniques have improved the analysis of curvature and geodesics in Finsler manifolds, fostering deeper insights into geometric flows and topology beyond Riemannian assumptions.
Conclusion: Choosing Between Finsler and Riemannian Geometry
Choosing between Finsler and Riemannian geometry depends on the complexity and generality of the metric structure needed; Riemannian geometry suits problems requiring isotropic and quadratic metrics, essential in classical physics and standard relativity. Finsler geometry generalizes this by allowing directional dependence and non-quadratic metrics, making it ideal for advanced fields like anisotropic media, biology, and generalized spacetime theories. The decision hinges on whether the application demands the simpler, well-understood Riemannian framework or the flexible, broader scope offered by Finsler structures.
Finsler Infographic
 libterm.com
libterm.com