Indecomposable objects are fundamental in various branches of mathematics, representing elements that cannot be expressed as a combination of simpler components. Understanding their structure helps in areas like algebra, representation theory, and module theory by revealing the building blocks of more complex entities. Explore the rest of the article to deepen your knowledge of indecomposable elements and their critical role in mathematical frameworks.
Table of Comparison
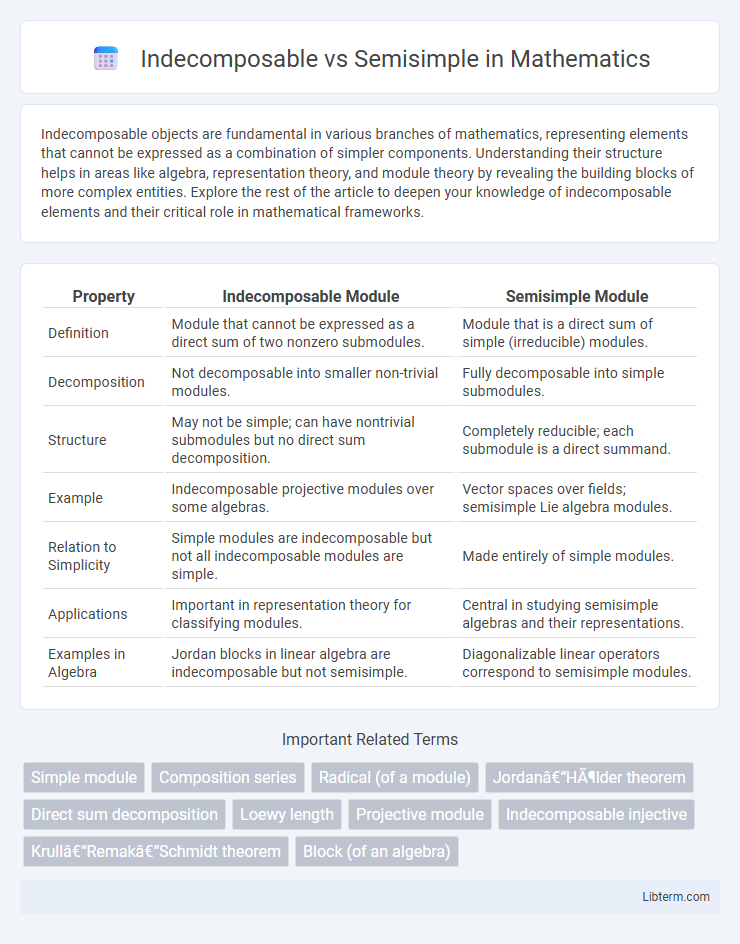
| Property | Indecomposable Module | Semisimple Module |
|---|---|---|
| Definition | Module that cannot be expressed as a direct sum of two nonzero submodules. | Module that is a direct sum of simple (irreducible) modules. |
| Decomposition | Not decomposable into smaller non-trivial modules. | Fully decomposable into simple submodules. |
| Structure | May not be simple; can have nontrivial submodules but no direct sum decomposition. | Completely reducible; each submodule is a direct summand. |
| Example | Indecomposable projective modules over some algebras. | Vector spaces over fields; semisimple Lie algebra modules. |
| Relation to Simplicity | Simple modules are indecomposable but not all indecomposable modules are simple. | Made entirely of simple modules. |
| Applications | Important in representation theory for classifying modules. | Central in studying semisimple algebras and their representations. |
| Examples in Algebra | Jordan blocks in linear algebra are indecomposable but not semisimple. | Diagonalizable linear operators correspond to semisimple modules. |
Introduction to Indecomposable and Semisimple Modules
Indecomposable modules are modules that cannot be expressed as a direct sum of two non-zero submodules, serving as fundamental building blocks in module theory. Semisimple modules decompose into a direct sum of simple modules, each having no proper non-zero submodules, reflecting a highly structured and well-understood class. Understanding the distinction between indecomposable and semisimple modules is essential for analyzing module decompositions and representation theory over rings.
Defining Indecomposable Modules
Indecomposable modules are modules that cannot be expressed as a direct sum of two non-zero submodules, representing the atomic building blocks in the module category. Semisimple modules, on the other hand, are modules that are direct sums of simple modules, implying every submodule has a complement. The distinction lies in indecomposables potentially having nontrivial endomorphisms and extensions, whereas semisimple modules are completely reducible with a straightforward structure.
Understanding Semisimple Modules
Semisimple modules decompose into a direct sum of simple modules, making their structure completely reducible and easy to analyze. Unlike indecomposable modules, which cannot be expressed as a direct sum of two nonzero submodules, semisimple modules exhibit maximal decomposability linked to their internal simplicity. This complete reducibility of semisimple modules plays a crucial role in representation theory and module classification, facilitating a clearer understanding of algebraic structures.
Key Differences between Indecomposable and Semisimple
Indecomposable modules cannot be expressed as a direct sum of two non-zero submodules, whereas semisimple modules are direct sums of simple modules. Indecomposable objects have a unique structure resistant to decomposition, while semisimple objects decompose fully into simple components. The classification of modules heavily relies on distinguishing indecomposable modules for internal structure and semisimple modules for straightforward decompositions.
Examples of Indecomposable Structures
Indecomposable structures include modules like the Jordan block in linear algebra, which cannot be expressed as a direct sum of smaller invariant subspaces. Another example is the indecomposable representation of quivers that fail to split into simpler subrepresentations. Such structures contrast with semisimple ones that decompose fully into simple modules or representations.
Properties of Semisimple Modules
Semisimple modules are characterized by their decomposition into direct sums of simple modules, ensuring complete reducibility without any nontrivial extensions. These modules exhibit the property that every submodule has a complementary submodule, allowing them to be expressed as a direct sum of minimal, indecomposable components. Unlike indecomposable modules, semisimple modules lack nontrivial submodules that cannot be further decomposed, making their structure easier to analyze in representation theory and module decomposition.
Indecomposable vs Semisimple in Representation Theory
Indecomposable representations in representation theory are modules that cannot be expressed as a direct sum of two nontrivial submodules, highlighting their structural simplicity. Semisimple representations, by contrast, completely decompose into a direct sum of simple modules, ensuring no further nontrivial decompositions exist. The distinction is crucial in understanding module categories over algebras, where indecomposable components serve as building blocks and semisimple modules represent fully reducible structures.
Applications in Algebra and Beyond
Indecomposable modules are fundamental in representation theory, serving as building blocks for more complex structures, while semisimple modules decompose neatly into direct sums of simple modules, facilitating the classification of algebraic objects. In algebraic geometry and number theory, understanding indecomposable and semisimple representations aids in analyzing Galois groups and vector bundles. Beyond pure algebra, these concepts find applications in quantum physics and coding theory, where the structure of modules influences the behavior of quantum states and error-correcting codes.
Common Misconceptions Clarified
Indecomposable modules are often mistakenly thought to be simple, but they can have nontrivial submodules without decomposing into direct sums. Semisimple modules are incorrectly assumed to be indecomposable, though they actually decompose into direct sums of simple modules. Clarifying this distinction is crucial for understanding module theory in algebra and avoiding common errors in representation analysis.
Summary and Further Reading
Indecomposable modules cannot be expressed as a direct sum of two nontrivial submodules, highlighting their fundamental role in module theory, while semisimple modules decompose entirely into simple submodules, emphasizing their structural clarity and ease of analysis. The distinction is crucial in representation theory and algebra, where understanding module decomposition aids in classifying representations of algebras and groups. For further reading, explore texts such as "Representations and Characters of Groups" by James and Liebeck and "Algebras and Representation Theory" by Assem, Simson, and Skowronski.
Indecomposable Infographic
 libterm.com
libterm.com