Minimal design emphasizes simplicity by focusing on essential elements and eliminating unnecessary details to create clean, functional spaces. This approach enhances clarity and fosters calm, making environments more inviting and easier to navigate. Discover how embracing minimalism can transform your space by reading the full article.
Table of Comparison
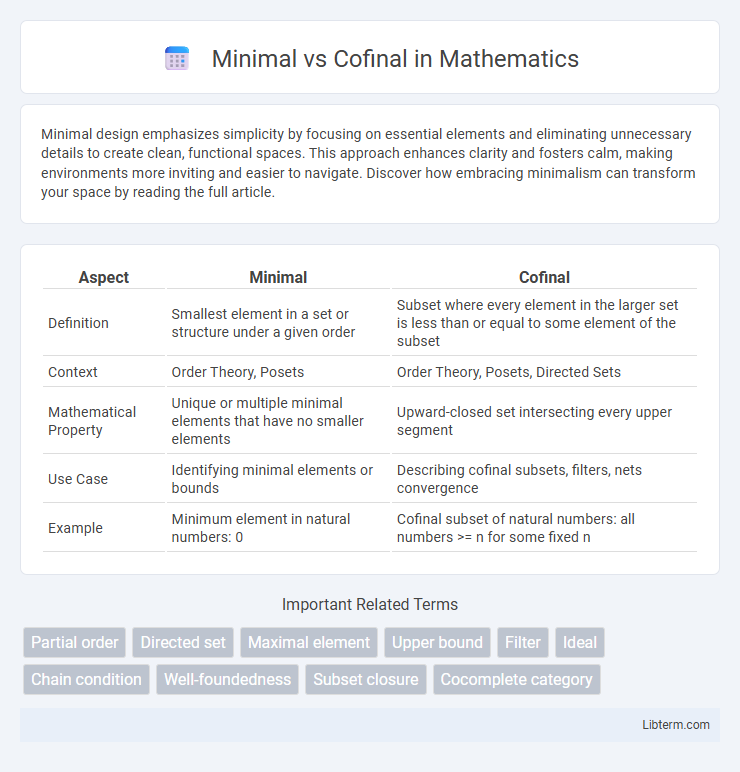
| Aspect | Minimal | Cofinal |
|---|---|---|
| Definition | Smallest element in a set or structure under a given order | Subset where every element in the larger set is less than or equal to some element of the subset |
| Context | Order Theory, Posets | Order Theory, Posets, Directed Sets |
| Mathematical Property | Unique or multiple minimal elements that have no smaller elements | Upward-closed set intersecting every upper segment |
| Use Case | Identifying minimal elements or bounds | Describing cofinal subsets, filters, nets convergence |
| Example | Minimum element in natural numbers: 0 | Cofinal subset of natural numbers: all numbers >= n for some fixed n |
Introduction to Minimal and Cofinal Concepts
Minimal elements are those in a partially ordered set that have no smaller elements preceding them, representing the foundational points within the order structure. Cofinal sets consist of elements that are unbounded above, meaning every element in the set has an upper bound within the cofinal subset. Understanding minimal and cofinal concepts is essential for analyzing order theory and lattice structures, where minimal elements identify starting points and cofinal subsets capture growth or extension behavior.
Defining Minimal Sets: Key Characteristics
Minimal sets are defined by the property that no proper subset satisfies the same conditions, highlighting their irreducibility in set theory and computer science. Key characteristics include uniqueness within the system, non-redundancy, and serving as foundational building blocks for more complex structures. These sets play a crucial role in optimization problems and formal logic where minimal solutions represent the simplest or most efficient configurations.
Understanding Cofinal Sets: Core Principles
Cofinal sets are subsets of a partially ordered set that intersect every upper segment of the set, ensuring coverage of all elements beyond certain bounds in the order. They play a crucial role in order theory by providing a framework to analyze the structure and behavior of infinite sequences and directed sets. Understanding cofinal sets involves recognizing how they compare with minimal sets, where cofinal sets capture maximal reach within the order, whereas minimal sets focus on the smallest elements with specific properties.
Mathematical Foundations of Minimality
Minimality in mathematics refers to the property of an object having no proper subobject with the same property, often studied in algebra, order theory, and topology to understand foundational structures. Cofinality concerns the least ordinal or smallest subset that is unbounded in a partially ordered set, crucial for analyzing the structure of infinite sets and ordinal numbers. The mathematical foundations of minimality explore how minimal elements serve as building blocks or irreducible components, contrasting with cofinal subsets that capture the essence of "direction" or "growth" within ordered frameworks.
The Role of Cofinality in Set Theory
Cofinality in set theory measures the smallest order type of an unbounded subset within a partially ordered set, playing a crucial role in classifying infinite cardinals and ordinals. Unlike minimal elements that represent the least element under a given order, cofinality identifies how a set can be approached through smaller subsets, influencing properties such as limit ordinals and cardinal arithmetic. Understanding cofinality aids in analyzing the structure of ordinals, particularly in distinguishing regular and singular cardinals, impacting foundational aspects of transfinite induction and recursion.
Comparing Minimal and Cofinal Structures
Minimal structures represent the simplest or least complex form within a partially ordered set, containing elements that have no smaller elements beneath them. Cofinal structures, in contrast, consist of subsets that intersect every larger element in the set, effectively capturing an unbounded growth or coverage within the order. Comparing minimal and cofinal structures highlights their dual roles in order theory: minimal elements define foundational baselines, while cofinal subsets ensure comprehensive reach throughout the entire set.
Applications of Minimal and Cofinal Elements
Minimal elements in partially ordered sets are crucial in optimization problems where identifying least elements guarantees the efficiency of algorithms in scheduling and resource allocation. Cofinal elements are essential in model theory and set theory for constructing chains and directed systems, enabling the analysis of infinite structures and ordinal numbers. Practical applications of minimal elements appear in database theory for query optimization, while cofinal elements support proofs in topology and the study of limits in category theory.
Advantages and Limitations of Each Approach
Minimal approaches prioritize simplicity and efficiency by using the least necessary components, reducing computational overhead and minimizing potential errors, which benefits systems requiring quick response times. However, minimal methods may lack flexibility and adaptability, limiting their effectiveness in complex or evolving environments. Cofinal approaches emphasize completeness and thoroughness, enabling comprehensive coverage of scenarios and improved robustness, yet they often involve increased complexity and resource consumption, which can hinder performance in time-sensitive applications.
Real-World Examples of Minimal vs Cofinal Use
Minimal sets appear prominently in network design where the least number of nodes ensure complete connectivity, such as minimal spanning trees in communication networks. Cofinal subsets emerge in economic models to describe agent behaviors where preferences or strategies eventually cover all possible outcomes, ensuring no option is omitted over time. These concepts highlight how minimal structures optimize resources while cofinal sets guarantee comprehensive reach in ordered systems.
Conclusion: Choosing Between Minimal and Cofinal
Selecting between minimal and cofinal elements depends heavily on the structure of the partially ordered set (poset) and the specific problem requirements. Minimal elements provide foundational starting points without predecessors, ideal for baseline analyses or initial conditions. Cofinal elements, encompassing maximal bounding conditions within posets, suit comprehensive coverage and ensure that every element is beneath or equal to some cofinal element in hierarchy-driven contexts.
Minimal Infographic
 libterm.com
libterm.com