A simple module is a fundamental concept in algebra, defined as a module that has no proper nonzero submodules. Understanding simple modules helps you grasp the building blocks of module theory, revealing structural insights about rings and their representations. Explore the rest of the article to deepen your knowledge of simple modules and their applications.
Table of Comparison
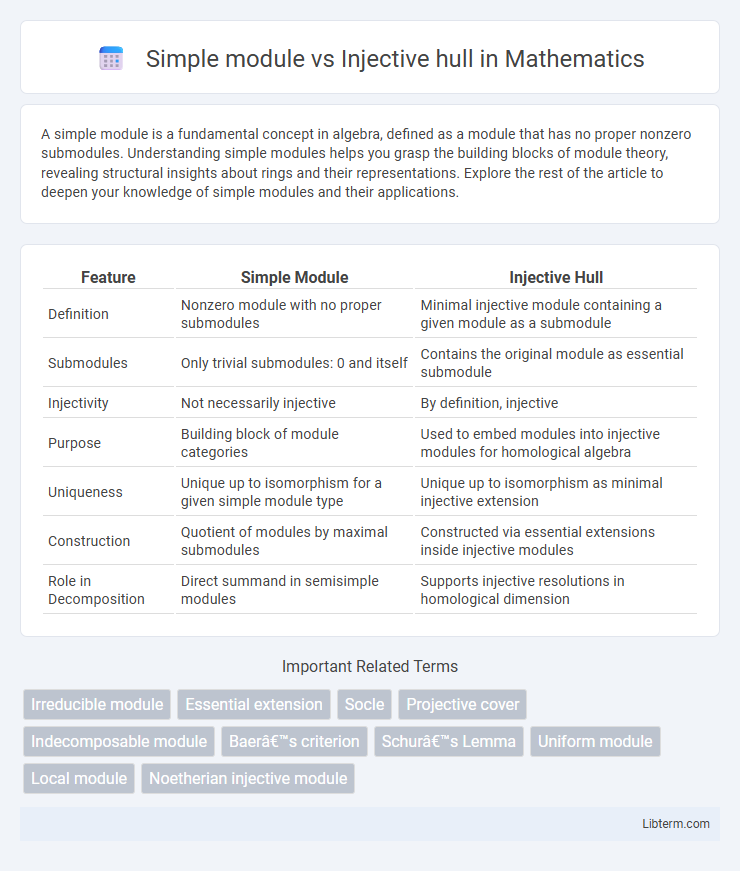
| Feature | Simple Module | Injective Hull |
|---|---|---|
| Definition | Nonzero module with no proper submodules | Minimal injective module containing a given module as a submodule |
| Submodules | Only trivial submodules: 0 and itself | Contains the original module as essential submodule |
| Injectivity | Not necessarily injective | By definition, injective |
| Purpose | Building block of module categories | Used to embed modules into injective modules for homological algebra |
| Uniqueness | Unique up to isomorphism for a given simple module type | Unique up to isomorphism as minimal injective extension |
| Construction | Quotient of modules by maximal submodules | Constructed via essential extensions inside injective modules |
| Role in Decomposition | Direct summand in semisimple modules | Supports injective resolutions in homological dimension |
Introduction to Simple Modules and Injective Hulls
Simple modules are modules over a ring that contain no proper non-zero submodules, making them the building blocks for module theory through composition series. Injective hulls represent the smallest injective module containing a given module as a submodule, serving as essential tools for extending modules while preserving homomorphic properties. Understanding simple modules and their injective hulls is fundamental in homological algebra and module classification, facilitating deeper insights into module extensions and decompositions.
Defining Simple Modules: Key Properties
Simple modules are modules over a ring that contain no nontrivial submodules, making them the building blocks of module theory. Each simple module has the property that every nonzero element generates the entire module, ensuring irreducibility. Injective hulls, on the other hand, provide minimal injective extensions of modules, often used to study embeddings of simple modules within larger, more complex structures.
Understanding Injective Hulls: Core Concepts
The injective hull of a module is the smallest injective module containing it as a submodule, providing a minimal essential extension that preserves injectivity properties. Simple modules serve as atomic building blocks in module theory, while injective hulls enable the embedding of these modules into larger structures that admit homomorphic extension properties. Understanding injective hulls involves recognizing essential extensions and the role they play in decompositions and homological algebra contexts.
Differences Between Simple Modules and Injective Hulls
Simple modules contain no proper nonzero submodules, representing minimal building blocks in module theory, while injective hulls are the smallest injective modules containing a given module as a submodule. A simple module is characterized by its irreducibility and minimality, whereas an injective hull ensures maximal extension and injectivity, often used to study module embeddings and essential extensions. The difference lies in simplicity versus injective maximality: simple modules have minimal substructure, and injective hulls provide essential, maximal injective envelopes.
Construction of Injective Hulls for Simple Modules
The construction of injective hulls for simple modules involves embedding a simple module into an injective module that contains it as an essential submodule, ensuring minimality and uniqueness up to isomorphism. Over a ring R, every simple module S has an injective hull E(S), which can be explicitly constructed using Baer's criterion by extending homomorphisms to injective envelopes. This process leverages the essential extension property to build E(S) as the smallest injective module that fully captures the structure of S while maintaining injectivity.
Examples Illustrating Simple Modules and Their Injective Hulls
Simple modules are modules with no proper nonzero submodules, such as the field \( k \) viewed as a module over itself or \( \mathbb{Z}/p\mathbb{Z} \) as a simple module over \( \mathbb{Z} \). The injective hull of a simple module provides the smallest injective module containing it; for example, the injective hull of \( \mathbb{Z}/p\mathbb{Z} \) as a \( \mathbb{Z} \)-module is the Prufer \( p \)-group \( \mathbb{Z}(p^\infty) \). In the category of \( k \)-vector spaces, every simple module is injective, demonstrating cases where the simple module and its injective hull coincide.
Significance in Module Theory and Algebra
Simple modules provide the foundational building blocks in module theory, representing modules with no proper submodules and enabling classification of more complex structures. Injective hulls serve as minimal injective extensions that preserve essential submodule properties while facilitating homological algebra techniques like exact sequences and decompositions. Both concepts are crucial for understanding module categories, with simple modules highlighting irreducibility and injective hulls ensuring completeness and extensibility in algebraic analysis.
Applications of Simple Modules and Injective Hulls
Simple modules serve as building blocks in module theory, offering critical insights in the classification of modules over rings and facilitating the decomposition of more complex modules. Injective hulls provide minimal injective extensions, essential for studying homological dimensions and exactness properties in module categories. Applications include representation theory, where simple modules classify irreducible representations, and homological algebra, where injective hulls are used to compute injective resolutions and derive functors such as Ext and Tor.
Challenges in Computing Injective Hulls
Computing injective hulls presents significant challenges due to their complexity and the intricate structure of injective modules, which often necessitates detailed knowledge of module decompositions and extensions. Unlike simple modules that are minimal and highly structured, injective hulls can be large and difficult to explicitly construct, especially over non-Noetherian rings or in infinite-dimensional cases. Algorithmic approaches must handle extensive homological algebra computations and the often non-unique embeddings into injective envelopes, complicating practical implementation in computational algebra systems.
Summary and Future Perspectives
Simple modules represent the fundamental building blocks in module theory, characterized by having no proper submodules, while injective hulls provide the minimal injective extension containing a given module. Research continues to explore the intricate relationships between these concepts, particularly in classifying modules over different rings and understanding their homological dimensions. Future advancements may leverage categorical approaches and computational methods to further clarify the structure and applications of simple modules and their injective hulls in representation theory and algebraic geometry.
Simple module Infographic
 libterm.com
libterm.com