Hausdorff measure extends the concept of length, area, and volume to irregular and fractal sets by using a dimension parameter that can be non-integer. It captures the size of a set in a way that conventional measures fail, making it essential for analyzing complex geometric structures in both pure and applied mathematics. Discover how Hausdorff measure applies to your work and explore its mathematical foundations in the rest of this article.
Table of Comparison
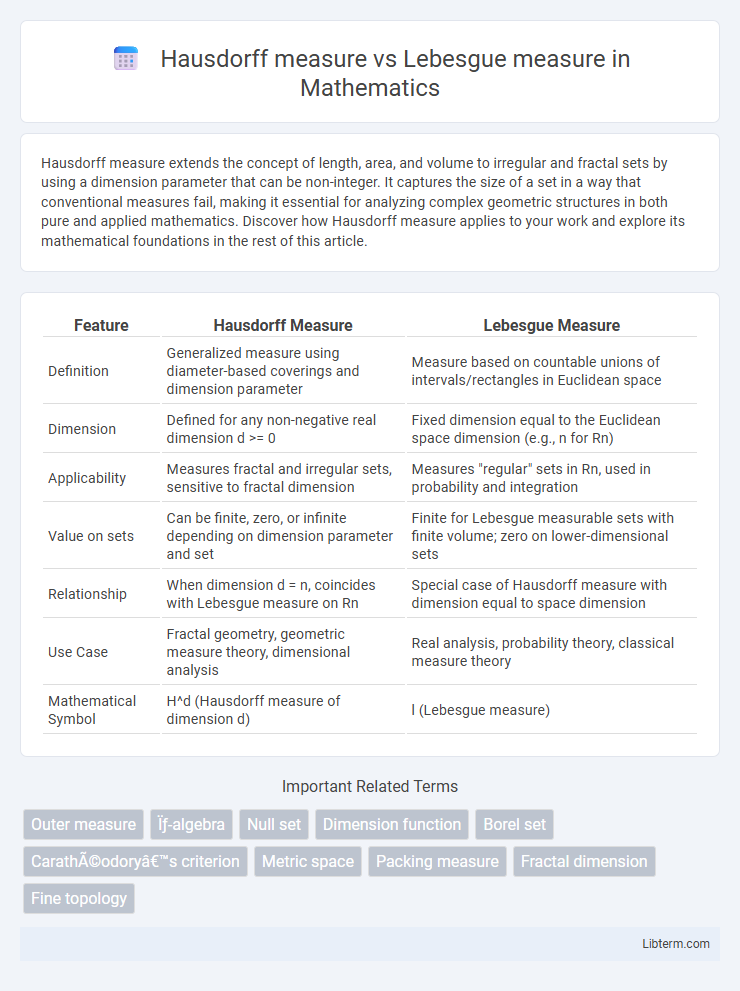
| Feature | Hausdorff Measure | Lebesgue Measure |
|---|---|---|
| Definition | Generalized measure using diameter-based coverings and dimension parameter | Measure based on countable unions of intervals/rectangles in Euclidean space |
| Dimension | Defined for any non-negative real dimension d >= 0 | Fixed dimension equal to the Euclidean space dimension (e.g., n for Rn) |
| Applicability | Measures fractal and irregular sets, sensitive to fractal dimension | Measures "regular" sets in Rn, used in probability and integration |
| Value on sets | Can be finite, zero, or infinite depending on dimension parameter and set | Finite for Lebesgue measurable sets with finite volume; zero on lower-dimensional sets |
| Relationship | When dimension d = n, coincides with Lebesgue measure on Rn | Special case of Hausdorff measure with dimension equal to space dimension |
| Use Case | Fractal geometry, geometric measure theory, dimensional analysis | Real analysis, probability theory, classical measure theory |
| Mathematical Symbol | H^d (Hausdorff measure of dimension d) | l (Lebesgue measure) |
Introduction to Measure Theory
Hausdorff measure extends Lebesgue measure by incorporating a dimensional parameter, enabling the measurement of fractal and irregular sets that Lebesgue measure cannot accurately capture. In measure theory, Lebesgue measure is designed for subsets of Euclidean space with integer dimensions, providing a standardized way to assign volume, area, or length. Hausdorff measure generalizes this concept, allowing the analysis of sets with non-integer Hausdorff dimensions, thus offering a finer tool for quantifying complex geometric structures.
Defining the Lebesgue Measure
The Lebesgue measure defines the standard way to assign a measure to subsets of Euclidean space, focusing on the length, area, or volume in n-dimensional spaces. It is constructed by covering sets with countable collections of intervals (or rectangles) and taking the infimum of the sums of their volumes, ensuring countable additivity and completeness. Unlike the Hausdorff measure, which generalizes dimension through scaling by diameters of sets, the Lebesgue measure aligns exactly with the intuitive geometric notion of size in \(\mathbb{R}^n\).
Understanding the Hausdorff Measure
Hausdorff measure generalizes the concept of length, area, and volume by assigning a measure to subsets of a metric space based on their fractal dimension, unlike Lebesgue measure which is limited to integer dimensions. It uses a scaling parameter called the dimension parameter \( d \) and covers the set with countable collections of sets whose diameters tend to zero, measuring the size in a way that captures the geometric complexity of irregular or fragmented sets. This makes Hausdorff measure essential for analyzing fractals, where traditional Lebesgue measure often fails to provide meaningful results.
Key Differences Between Lebesgue and Hausdorff Measures
Lebesgue measure is primarily designed to measure subsets of Euclidean space with integer dimensions, assigning volume in a way consistent with conventional notions of length, area, and volume. Hausdorff measure generalizes Lebesgue measure to non-integer dimensions, effectively quantifying the size of fractals and irregular geometric sets through a dimensional parameter. Unlike Lebesgue measure, which is additive and suitable for well-behaved sets, Hausdorff measure captures fine geometric detail and scale invariance, making it essential for analyzing sets with complex structures.
Mathematical Properties of Lebesgue Measure
Lebesgue measure is a complete, translation-invariant measure defined on the sigma-algebra of Lebesgue measurable sets in Euclidean space, assigning the intuitive notion of volume to subsets. It is countably additive and regular, facilitating the integration of a broader class of functions compared to Riemann integration. Unlike Hausdorff measure, which generalizes dimension and measures fractal sets, Lebesgue measure primarily applies to sets with integer dimension and serves as the foundation for modern analysis and probability theory.
Mathematical Properties of Hausdorff Measure
Hausdorff measure extends Lebesgue measure by quantifying the size of fractal and irregular sets based on their dimensional scaling properties, using a parameter called the Hausdorff dimension. Unlike Lebesgue measure, which is primarily defined for integer dimensions and standard geometric sets, Hausdorff measure applies to any non-negative real dimension, enabling precise measurement of complex geometrical structures. It is countably subadditive, monotone, and invariant under isometries, making it a fundamental tool in geometric measure theory and fractal geometry.
Applications of Lebesgue Measure in Analysis
Lebesgue measure plays a crucial role in real analysis by providing a foundation for integrating functions over complex sets with irregular boundaries, enabling the development of Lebesgue integration. Its applications include studying convergence theorems, such as the Dominated Convergence Theorem, and facilitating the precise formulation of function spaces like L^p spaces crucial for partial differential equations and harmonic analysis. Compared to Hausdorff measure, which generalizes measure to fractal and lower-dimensional sets, Lebesgue measure remains the standard tool for measuring volumes and integrating functions on Euclidean spaces.
Applications of Hausdorff Measure in Fractal Geometry
Hausdorff measure provides a powerful tool for quantifying fractal dimensions, capturing the intricate scaling properties of sets that traditional Lebesgue measure cannot measure effectively. It is essential in fractal geometry for calculating dimensions of objects with complex, self-similar structures, such as the Mandelbrot set or Cantor dust. This measure allows mathematicians and scientists to rigorously analyze and compare fractal sets by assigning a dimension that reflects their geometric complexity beyond integer values.
Examples Illustrating Both Measures
The Lebesgue measure assigns the length, area, or volume to standard geometric shapes such as intervals, rectangles, and cubes in Euclidean spaces, exemplified by the unit interval [0,1] having Lebesgue measure 1. In contrast, the Hausdorff measure generalizes beyond integer dimensions to fractal sets, such as the Cantor set, which has zero Lebesgue measure but a positive Hausdorff measure corresponding to its fractal dimension. These examples highlight Lebesgue measure's suitability for regular sets and Hausdorff measure's effectiveness in capturing the size of irregular or fractal structures.
Choosing the Appropriate Measure: Use Cases and Summary
Hausdorff measure is ideal for analyzing fractal sets, irregular geometric shapes, and dimension theory, providing precise scaling properties on non-integer dimensional objects. Lebesgue measure excels in measuring volume, area, and length of regular sets in Euclidean space, supporting integral definitions and classical calculus applications. Selecting the appropriate measure depends on the set's structural complexity and dimensionality, with Hausdorff measure capturing fine geometric detail and Lebesgue measure delivering simplicity for standard measurable sets.
Hausdorff measure Infographic
 libterm.com
libterm.com