The null set, also known as the empty set, is a fundamental concept in mathematics representing a set with no elements. It serves as the foundation for set theory and is denoted by the symbol . Discover more about the properties and applications of the null set in the rest of the article.
Table of Comparison
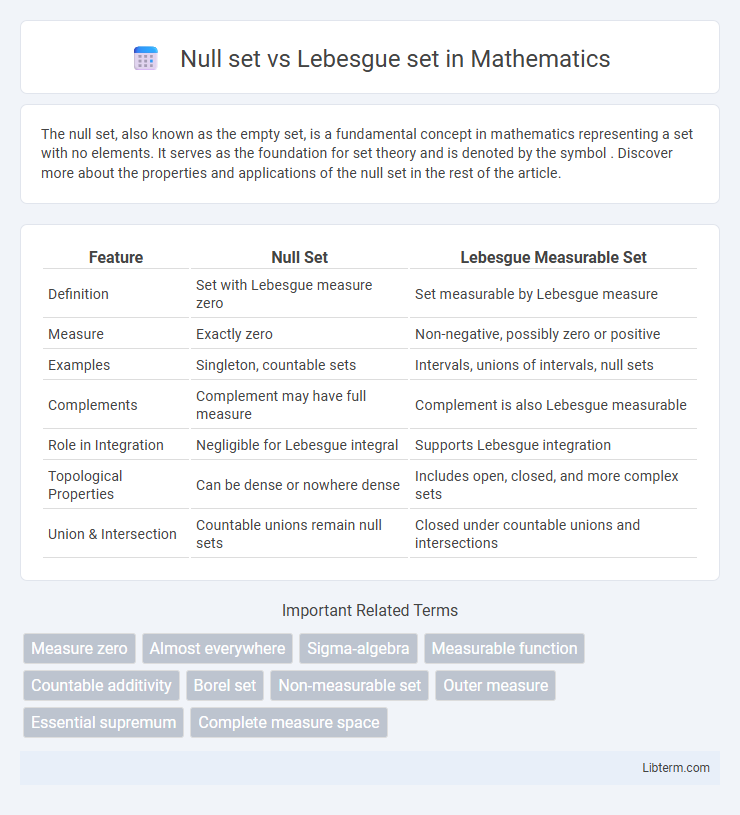
| Feature | Null Set | Lebesgue Measurable Set |
|---|---|---|
| Definition | Set with Lebesgue measure zero | Set measurable by Lebesgue measure |
| Measure | Exactly zero | Non-negative, possibly zero or positive |
| Examples | Singleton, countable sets | Intervals, unions of intervals, null sets |
| Complements | Complement may have full measure | Complement is also Lebesgue measurable |
| Role in Integration | Negligible for Lebesgue integral | Supports Lebesgue integration |
| Topological Properties | Can be dense or nowhere dense | Includes open, closed, and more complex sets |
| Union & Intersection | Countable unions remain null sets | Closed under countable unions and intersections |
Understanding the Null Set: Definition and Basics
A null set, also known as a measure-zero set, is a subset of a measure space whose Lebesgue measure equals zero, meaning it occupies no "volume" in the space despite possibly containing infinitely many points. Understanding the null set involves recognizing that it forms the foundation for Lebesgue integration, allowing functions to be equal almost everywhere while differing on sets of measure zero without affecting integrals. This concept contrasts with Lebesgue measurable sets, which are those sets for which the Lebesgue measure is well-defined and include null sets as special cases with measure zero.
Introduction to Lebesgue Sets in Measure Theory
Lebesgue sets are fundamental in measure theory, representing measurable sets with well-defined Lebesgue measure, unlike null sets which have measure zero and no volume in the Lebesgue sense. These sets form the basis for Lebesgue integration, allowing for the generalization of classical Riemann integration by accommodating functions with more complex discontinuities. Understanding Lebesgue sets enables precise handling of measurable functions and contributes to advanced analysis in probability, real analysis, and mathematical physics.
Key Differences Between Null Sets and Lebesgue Sets
Null sets are subsets of real numbers with Lebesgue measure zero, meaning they occupy no "volume" in the measure-theoretic sense. Lebesgue sets, in contrast, refer to measurable sets where the Lebesgue integral is well-defined, encompassing all sets with finite or infinite measure, not necessarily zero. The key difference lies in null sets having measure zero and negligible size, whereas Lebesgue sets include all measurable sets regardless of their measure, playing a critical role in defining integration and measure theory.
Properties and Examples of Null Sets
Null sets, also known as measure zero sets, are subsets of a given space that can be covered by countably many intervals whose total length sums to zero, exhibiting properties such as having zero Lebesgue measure and being negligible in integration theory. Examples include single points, countable sets like the rationals, and Cantor sets, each having Lebesgue measure zero despite possible complex structures. Unlike Lebesgue measurable sets, null sets do not affect the value of Lebesgue integrals, allowing them to serve as a foundation for defining almost everywhere properties in real analysis.
Exploring the Characteristics of Lebesgue Measurable Sets
Lebesgue measurable sets extend beyond null sets by including any set whose symmetric difference with a Borel set has measure zero, enabling a broader framework for integration theory. These sets maintain closure under countable unions and intersections, crucial for establishing the Lebesgue measure's completeness. Understanding the interplay between null sets and Lebesgue measurable sets highlights how measure theory accommodates complex subsets of the real line in analysis.
Measure Zero: The Role in Both Null and Lebesgue Sets
Measure zero plays a crucial role in differentiating null sets and Lebesgue sets by quantifying the "size" of subsets within a given space. Null sets are defined as sets with Lebesgue measure zero, implying that these sets occupy no volume in the measure-theoretic sense. In contrast, Lebesgue sets involve measurable sets where the concept of density and measure zero subsets helps characterize points of approximate continuity for measurable functions.
Set Operations: Null Sets vs Lebesgue Sets
Null sets have measure zero in Lebesgue measure theory, meaning their union or intersection with any measurable set does not affect the set's measure. Lebesgue sets are measurable sets where the Lebesgue differentiation theorem applies, often involving operations like countable unions or intersections that preserve measurability. Set operations on null sets generally maintain nullity, while operations on Lebesgue sets preserve measure properties critical for integration and analysis.
Applications in Real Analysis and Probability
Null sets are crucial in real analysis for defining almost everywhere properties, enabling the rigorous treatment of functions that differ only on sets of measure zero, which ensures integrals and limits remain stable. Lebesgue measurable sets, which can have positive measure, form the foundation of Lebesgue integration, extending Riemann integrals and allowing integration of a wider class of functions. In probability theory, null sets correspond to events with zero probability, while Lebesgue measurable sets represent the valid measurable events in continuous probability spaces, facilitating the formal definition of probability measures and expectations.
Common Misconceptions About Null and Lebesgue Sets
Null sets, often misunderstood as simply "empty" or negligible, actually refer to sets of measure zero in Lebesgue measure, meaning their total length, area, or volume is zero, even if they contain infinitely many points. Lebesgue measurable sets include all null sets but also encompass more complex sets that can be approximated by open or closed intervals, ensuring well-defined measures. A common misconception is that all subsets of null sets must be null themselves, but non-measurable subsets can exist, emphasizing the subtle distinctions in measure theory.
Summary: Choosing Between Null Sets and Lebesgue Sets
Null sets have measure zero and are critical in measure theory for identifying negligible subsets in spaces. Lebesgue sets provide a framework for integrating functions with respect to the Lebesgue measure, capturing more intricate structures than null sets alone. Selecting between null sets and Lebesgue sets hinges on whether the focus is on measure-zero exceptions or on sets suitable for Lebesgue integration and detailed function analysis.
Null set Infographic
 libterm.com
libterm.com