A local ring is a commutative ring with a unique maximal ideal, making it a fundamental structure in algebraic geometry and commutative algebra. Its properties help analyze algebraic varieties and modules at specific points, providing deep insights into local behavior. Explore the rest of the article to understand how local rings play a crucial role in mathematical theory and applications.
Table of Comparison
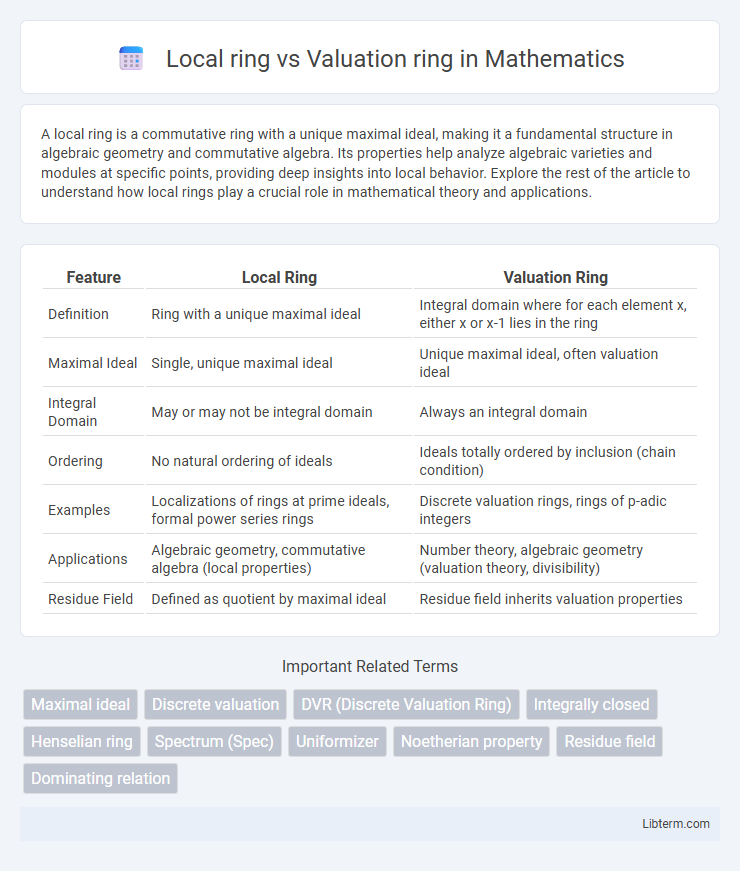
| Feature | Local Ring | Valuation Ring |
|---|---|---|
| Definition | Ring with a unique maximal ideal | Integral domain where for each element x, either x or x-1 lies in the ring |
| Maximal Ideal | Single, unique maximal ideal | Unique maximal ideal, often valuation ideal |
| Integral Domain | May or may not be integral domain | Always an integral domain |
| Ordering | No natural ordering of ideals | Ideals totally ordered by inclusion (chain condition) |
| Examples | Localizations of rings at prime ideals, formal power series rings | Discrete valuation rings, rings of p-adic integers |
| Applications | Algebraic geometry, commutative algebra (local properties) | Number theory, algebraic geometry (valuation theory, divisibility) |
| Residue Field | Defined as quotient by maximal ideal | Residue field inherits valuation properties |
Introduction to Local Rings and Valuation Rings
Local rings are commutative rings with a unique maximal ideal, essential in algebraic geometry and commutative algebra for studying local properties of algebraic varieties and schemes. Valuation rings are a specific type of local ring characterized by a total ordering of ideals, providing a framework to measure elements' divisibility and serve as key tools in valuation theory and algebraic number theory. Both structures are foundational in understanding local behavior in rings, with valuation rings refining the concept of local rings by incorporating value-based divisibility conditions.
Defining Local Rings
Local rings are commutative rings with a unique maximal ideal, which simplifies their structure and facilitates localization in algebraic geometry and commutative algebra. Valuation rings are a special class of local rings characterized by their valuation property, where every element or its inverse belongs to the ring, reflecting an order structure on the field. The defining feature of a local ring is the presence of only one maximal ideal, contrasting with valuation rings that impose additional valuation conditions to measure divisibility within the ring.
Defining Valuation Rings
A valuation ring is an integral domain in which for every element of its field of fractions, either the element or its inverse belongs to the ring, providing a total order on the ideals. Unlike a local ring, which merely requires a unique maximal ideal, a valuation ring's structure reflects a valuation assigning values to elements that embed into a totally ordered abelian group. This characterization of valuation rings plays a crucial role in algebraic geometry and number theory by encoding information about divisibility and valuation of elements in the field.
Key Properties of Local Rings
Local rings are commutative rings with a unique maximal ideal, ensuring all non-units form this ideal, which is crucial for algebraic geometry and commutative algebra. Valuation rings are a specialized type of local ring characterized by a total ordering on their ideals, reflecting valuation properties related to divisibility and absolute values. The key properties of local rings include their ability to localize algebraic structures, support dimension theory through Krull dimension, and enable the study of formal neighborhoods in schemes.
Key Properties of Valuation Rings
Valuation rings are integral local rings characterized by the property that for every element in their field of fractions, either the element or its inverse belongs to the ring, encoding a total ordering on the ideals. These rings are integrally closed and have a unique maximal ideal, with their value group providing a valuation that measures divisibility. Unlike arbitrary local rings, valuation rings ensure that all finitely generated ideals are principal or well-ordered, enabling a precise control over the ring's structure and rational function behavior.
Local Ring vs Valuation Ring: Structural Differences
Local rings possess a unique maximal ideal, providing a framework for studying algebraic structures near a point, whereas valuation rings extend local rings by incorporating a total ordering on value groups that measures the size of elements in a field. Structural differences lie in valuation rings being integrally closed local rings with valuation functions that encode divisibility properties, contrasting with general local rings which may lack such valuation structures. The hierarchy of ideals in valuation rings is totally ordered, reflecting their valuation nature, while local rings allow more complex, partially ordered ideal lattices.
Examples of Local Rings in Algebra
Local rings are commutative rings with a unique maximal ideal, exemplified by the ring of formal power series k[[x]] over a field k, where the maximal ideal consists of power series with zero constant term. Valuation rings serve as local rings arising from valuation theory, such as the ring of p-adic integers \(\mathbb{Z}_p\), characterized by a valuation defining divisibility properties and a unique maximal ideal generated by p. In algebra, examples of local rings include the localization of a ring \(R\) at a prime ideal \(P\), denoted \(R_P\), which sets all elements outside \(P\) as units, thus producing a local ring with maximal ideal \(P R_P\).
Examples of Valuation Rings in Algebra
Valuation rings, such as the ring of p-adic integers \(\mathbb{Z}_p\) and the ring of formal power series \(k[[t]]\) over a field \(k\), serve as key examples distinguishing them from general local rings by their totality in ordering ideals. Unlike local rings that simply have a unique maximal ideal, valuation rings impose a valuation that orders elements by divisibility, enabling applications like discrete valuation rings in number theory and algebraic geometry. These valuation rings exemplify how valuations characterize local properties while providing structure for completion and factorization in integral domains.
Applications in Algebraic Geometry and Number Theory
Local rings provide a foundational framework for studying singularities and local properties of algebraic varieties, enabling precise analysis of function behavior at specific points in algebraic geometry. Valuation rings play a crucial role in describing valuations and completions that facilitate resolution of singularities and local uniformization, essential tools in birational geometry and arithmetic geometry. In number theory, valuation rings underpin the construction of discrete valuation rings used in local field theory, aiding in the characterization of norms, places, and local-global principles.
Summary: Choosing Between Local and Valuation Rings
Local rings are commutative rings with a unique maximal ideal, often used to study algebraic varieties at specific points. Valuation rings generalize this concept by incorporating a valuation measuring element divisibility, providing a finer structure used in valuation theory and algebraic geometry. Selecting between local and valuation rings depends on the need for either localized algebraic information or a valuation-based hierarchical structure capturing element size and divisibility.
Local ring Infographic
 libterm.com
libterm.com