Weak convergence refers to a type of convergence in functional analysis where sequences of functions converge not pointwise but in terms of their integral properties against all continuous linear functionals. This concept is crucial in fields like probability theory and partial differential equations, helping to understand limits of distributions and weak solutions. Explore the rest of the article to deepen your understanding of weak convergence and its applications.
Table of Comparison
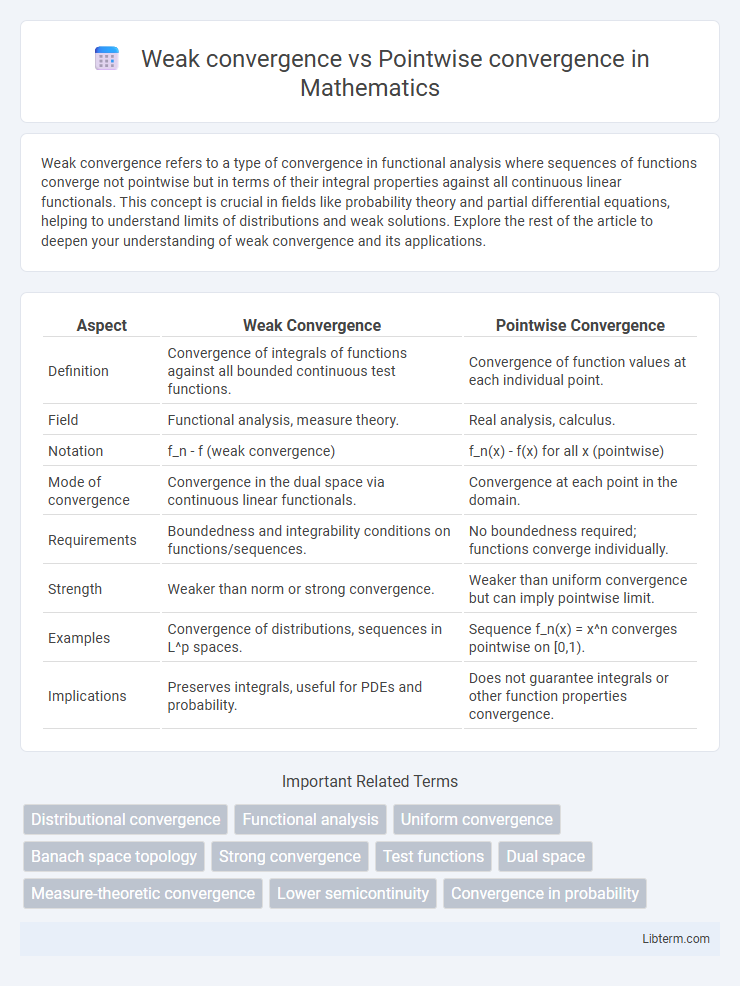
| Aspect | Weak Convergence | Pointwise Convergence |
|---|---|---|
| Definition | Convergence of integrals of functions against all bounded continuous test functions. | Convergence of function values at each individual point. |
| Field | Functional analysis, measure theory. | Real analysis, calculus. |
| Notation | f_n - f (weak convergence) | f_n(x) - f(x) for all x (pointwise) |
| Mode of convergence | Convergence in the dual space via continuous linear functionals. | Convergence at each point in the domain. |
| Requirements | Boundedness and integrability conditions on functions/sequences. | No boundedness required; functions converge individually. |
| Strength | Weaker than norm or strong convergence. | Weaker than uniform convergence but can imply pointwise limit. |
| Examples | Convergence of distributions, sequences in L^p spaces. | Sequence f_n(x) = x^n converges pointwise on [0,1). |
| Implications | Preserves integrals, useful for PDEs and probability. | Does not guarantee integrals or other function properties convergence. |
Introduction to Convergence in Mathematics
Weak convergence describes the convergence of functionals or sequences with respect to a weaker topology, typically involving integrals or distributions, making it essential in functional analysis and probability theory. Pointwise convergence occurs when a sequence of functions converges at each individual point in the domain, emphasizing local or direct behavior without necessarily preserving continuity or integrability. Understanding these forms of convergence is crucial for analyzing limits in infinite-dimensional spaces and ensuring appropriate function behavior in mathematical modeling.
Defining Pointwise Convergence
Pointwise convergence of a sequence of functions \((f_n)\) to a function \(f\) occurs when, for every fixed point \(x\), the sequence \(f_n(x)\) converges to \(f(x)\) as \(n\) approaches infinity. This type of convergence emphasizes behavior at individual points rather than on the entire domain simultaneously. Unlike weak convergence, pointwise convergence does not require integration or inner product structures, making it fundamental in real analysis and function approximation.
Understanding Weak Convergence
Weak convergence in functional analysis refers to a sequence of functions converging in the sense that their integrals against every continuous linear functional converge, contrasting with pointwise convergence where each function value converges individually. Understanding weak convergence involves recognizing how it captures a generalized form of convergence crucial in infinite-dimensional spaces, particularly in Hilbert and Banach spaces. This concept is fundamental in optimization, partial differential equations, and variational methods, where strong (pointwise) convergence may fail but weak convergence still yields meaningful limits.
Mathematical Formalism of Pointwise Convergence
Pointwise convergence of a sequence of functions \((f_n)_{n\in\mathbb{N}}\) to a function \(f\) on a domain \(D\) is defined by the condition that for every \(x \in D\), the sequence \((f_n(x))_{n\in\mathbb{N}}\) converges to \(f(x)\) as \(n \to \infty\). Mathematically, this is expressed as \(\forall x \in D, \lim_{n \to \infty} f_n(x) = f(x)\), emphasizing convergence at each individual point rather than uniform or integral criteria. Pointwise convergence contrasts with weak convergence, which involves convergence under integration against test functions or dual space elements, focusing instead on distributional or functional convergence rather than direct pointwise limits.
Formal Definition of Weak Convergence
Weak convergence in a Hilbert space refers to a sequence {x_n} converging to x if for every continuous linear functional f, the scalar sequence f(x_n) converges to f(x). This contrasts with pointwise convergence, where a sequence of functions {f_n} converges pointwise to f if for every point x in the domain, the values f_n(x) approach f(x). Formally, weak convergence hinges on the dual space interaction and is defined by the condition that
Key Differences Between Weak and Pointwise Convergence
Weak convergence involves convergence in the sense of distributions or test functions, where a sequence of functions converges if it converges under all continuous linear functionals, whereas pointwise convergence requires each function value to converge at every point independently. The key difference lies in the mode of convergence: weak convergence is more global and functional-based, making it suitable in functional analysis and PDEs, while pointwise convergence is local and purely value-based. Weak convergence can imply convergence in an average or integral sense without guaranteeing convergence at individual points, unlike pointwise convergence which demands exact convergence for each input.
Examples Illustrating Pointwise vs Weak Convergence
Pointwise convergence occurs when a sequence of functions f_n converges at each individual point x to a function f, such as f_n(x) = x^n on [0,1] converging pointwise to a function that is 0 on [0,1) and 1 at x=1. Weak convergence involves convergence in the distributional sense, for example, the sequence of Dirac delta approximations d_n(x) = n * kh_{[0,1/n]}(x) converges weakly to d_0 but does not converge pointwise. These examples highlight the difference where pointwise convergence requires exact value convergence at each point, while weak convergence requires convergence in action on test functions or integrals.
Applications in Functional Analysis
Weak convergence in functional analysis is pivotal for studying infinite-dimensional spaces where pointwise convergence fails to preserve structural properties of function sequences. Applications include optimization problems, partial differential equations, and the analysis of Banach and Hilbert spaces, where weak convergence ensures compactness and lower semicontinuity essential for existence theorems. Pointwise convergence, while intuitive for sequence evaluation, often lacks the robustness needed in these contexts, making weak convergence the preferred tool in variational methods and operator theory.
Implications in Real-World Problems
Weak convergence describes the behavior of sequences of probability measures or functions as they converge in distribution, impacting statistical inference by ensuring consistency of estimators under varying sample conditions. Pointwise convergence examines the limit of function values at every point, influencing numerical methods and algorithm stability where local accuracy is critical. Understanding the distinctions aids in selecting appropriate convergence criteria for modeling uncertainty, optimization algorithms, and real-world data approximations in engineering and finance.
Conclusion: Choosing the Appropriate Convergence Criterion
Selecting the appropriate convergence criterion depends on the context and goals of the analysis, with weak convergence being suitable for studying distributions of random variables and pointwise convergence apt for assessing function-by-function limits. Weak convergence ensures convergence in distribution, making it ideal for probabilistic and measure-theoretic applications, while pointwise convergence focuses on the behavior at individual points, which may not guarantee overall functional stability. Analysts must weigh the trade-offs between these types to ensure accurate interpretation of limiting behavior in statistical and functional settings.
Weak convergence Infographic
 libterm.com
libterm.com