Arc-connected spaces are topological spaces where any two points can be joined by a continuous curve, called an arc. This property ensures a strong form of connectivity that is fundamental in fields like algebraic topology and complex analysis. Explore the rest of the article to understand how arc-connectedness influences various mathematical structures and your understanding of continuity.
Table of Comparison
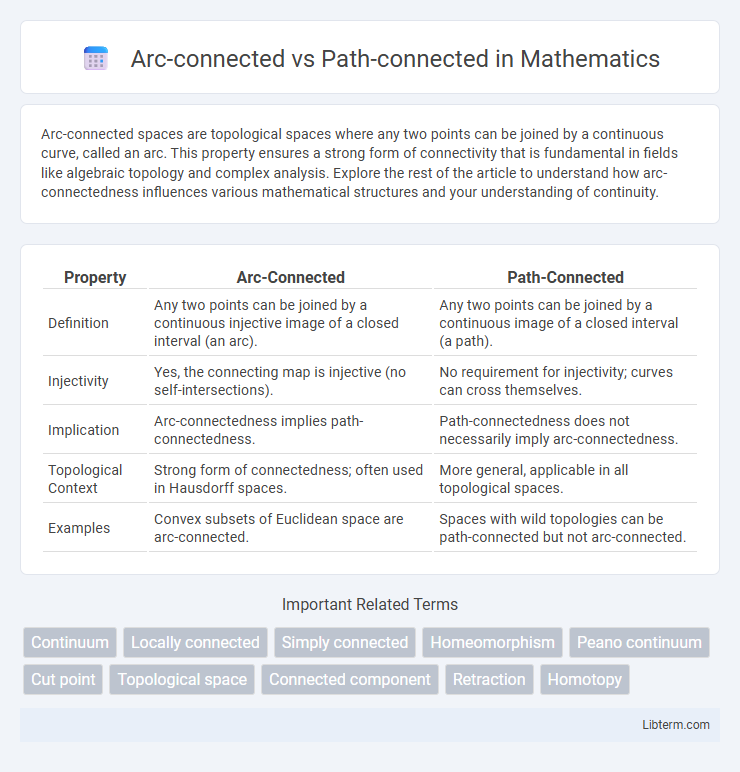
| Property | Arc-Connected | Path-Connected |
|---|---|---|
| Definition | Any two points can be joined by a continuous injective image of a closed interval (an arc). | Any two points can be joined by a continuous image of a closed interval (a path). |
| Injectivity | Yes, the connecting map is injective (no self-intersections). | No requirement for injectivity; curves can cross themselves. |
| Implication | Arc-connectedness implies path-connectedness. | Path-connectedness does not necessarily imply arc-connectedness. |
| Topological Context | Strong form of connectedness; often used in Hausdorff spaces. | More general, applicable in all topological spaces. |
| Examples | Convex subsets of Euclidean space are arc-connected. | Spaces with wild topologies can be path-connected but not arc-connected. |
Introduction to Arc-connected and Path-connected Spaces
Arc-connected spaces are topological spaces where any two points can be joined by a continuous image of a closed interval, called an arc, ensuring a stronger form of connectivity. Path-connected spaces allow any two points to be connected by a continuous path, which may not necessarily be an arc with injectivity, highlighting a fundamental difference in connectivity types. Understanding the distinction between arc-connected and path-connected spaces is essential in topology, as it influences the properties and classification of spaces in areas such as algebraic topology and geometric analysis.
Definitions of Arc-connected and Path-connected
Arc-connected spaces are topological spaces where any two points can be joined by an arc, which is a homeomorphic image of a closed interval [0,1], ensuring a continuous, injective mapping without self-intersections. Path-connected spaces allow any two points to be connected by a continuous path, a continuous function from [0,1] to the space, without the injectivity requirement. The key distinction lies in the injectivity constraint for arc-connectedness, making every arc-connected space path-connected, but not every path-connected space arc-connected.
Key Differences Between Arc-connected and Path-connected
Arc-connected spaces require a continuous injective map from the unit interval, ensuring a simple, non-overlapping curve between points, while path-connected spaces allow any continuous map, possibly with self-intersections. Every arc-connected space is path-connected, but the converse is not always true, highlighting the stricter nature of arc-connectedness in topology. This distinction is crucial in analyzing topological properties related to continuity and shape simplicity.
Examples of Arc-connected Spaces
Arc-connected spaces include familiar examples such as Euclidean spaces \(\mathbb{R}^n\), where any two points can be joined by a straight line segment, ensuring path and arc connectivity. Simple shapes like circles and polygons in the plane are arc-connected since continuous paths homeomorphic to an interval connect any two points. More complex examples include connected graphs and manifolds, which are locally arc-connected, allowing an arc between points through curves or piecewise linear paths.
Examples of Path-connected Spaces
Path-connected spaces include the Euclidean plane \(\mathbb{R}^2\), where any two points can be joined by a continuous path such as a straight line segment. Another example is the unit circle \(S^1\), in which any pair of points can be connected by a continuous arc along the circle itself. Unlike arc-connected spaces, path-connected spaces may have continuous paths without requiring the path to be an embedding, but in many common spaces like \(\mathbb{R}^n\) and \(S^1\), path-connectedness and arc-connectedness coincide.
Topological Properties and Implications
Arc-connected spaces guarantee the existence of a continuous injective map from a closed interval, linking any two points, ensuring stronger topological coherence than mere path-connectedness, which only requires a continuous map without injectivity. This distinction impacts fundamental topological properties such as local connectivity and homotopy type, with arc-connected spaces often facilitating simpler classification of components and robust extension properties for continuous functions. Key implications include differences in component decompositions and the behavior of continuous images, where arc-connected sets preserve more geometric information compared to general path-connected sets.
Common Misconceptions and Clarifications
Arc-connected and path-connected spaces are often confused as identical, but a key distinction is that arc-connectedness requires a continuous injective map (an arc) between points, whereas path-connectedness only needs a continuous map. A common misconception is believing every path-connected space is also arc-connected; however, certain topological spaces, like the topologist's sine curve, are path-connected without being arc-connected. Clarifying this distinction helps in understanding the subtleties of topological connectivity and the role of injectivity in forming arcs.
Applications in Mathematics and Topology
Arc-connected spaces, where any two points can be joined by a continuous injective image of an interval, allow stronger structural analysis in topology, essential for studying simple curves and manifolds. Path-connected spaces enable the use of homotopy theory and fundamental group computations, crucial for classifying topological spaces and continuous mappings. Both concepts are pivotal in algebraic topology, aiding in the analysis of connectedness properties in complex geometric and topological structures.
Theorems Relating Arc-connectedness and Path-connectedness
Arc-connectedness and path-connectedness are topological properties often analyzed through foundational theorems. A key theorem states that in a Hausdorff space, every arc-connected set is also path-connected, as arcs are injective continuous images of intervals. Another theorem establishes that in locally arc-connected spaces, path-connectedness and arc-connectedness coincide, ensuring every path can be approximated by arcs precisely connecting points.
Summary and Further Reading
Arc-connected spaces guarantee the existence of a continuous injective map from an interval into the space between any two points, ensuring a stronger form of connectedness than path-connected spaces, which only require a continuous map without injectivity. Both concepts are fundamental in topology, with arc-connectedness implying path-connectedness, but not vice versa; this distinction is crucial for understanding properties of complex topological spaces. For further reading, consult classic topology texts like Munkres' *Topology* or Engelking's *General Topology* to explore detailed proofs and applications of these connectivity concepts.
Arc-connected Infographic
 libterm.com
libterm.com