Adjunction is a fundamental concept in category theory that describes a relationship between two functors, often revealing deep structural insights within mathematics. Understanding how adjoint functors interact can clarify complex constructions and computations in algebra, topology, and beyond. Explore the rest of the article to see how adjunctions shape mathematical frameworks and influence your perspective on abstract relationships.
Table of Comparison
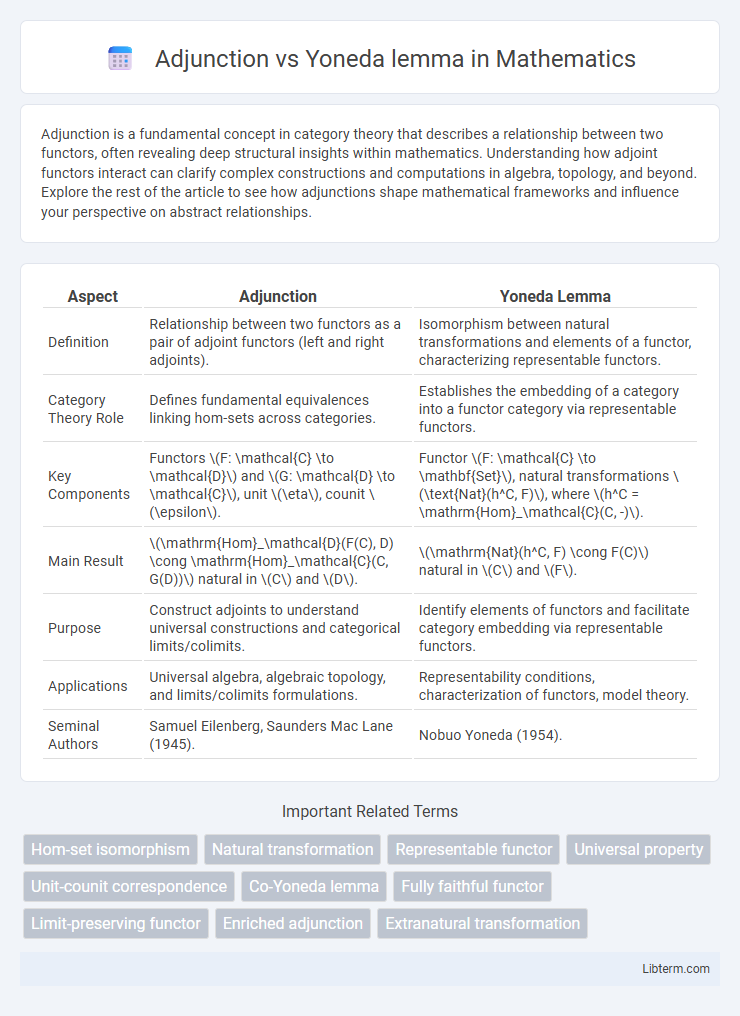
| Aspect | Adjunction | Yoneda Lemma |
|---|---|---|
| Definition | Relationship between two functors as a pair of adjoint functors (left and right adjoints). | Isomorphism between natural transformations and elements of a functor, characterizing representable functors. |
| Category Theory Role | Defines fundamental equivalences linking hom-sets across categories. | Establishes the embedding of a category into a functor category via representable functors. |
| Key Components | Functors \(F: \mathcal{C} \to \mathcal{D}\) and \(G: \mathcal{D} \to \mathcal{C}\), unit \(\eta\), counit \(\epsilon\). | Functor \(F: \mathcal{C} \to \mathbf{Set}\), natural transformations \(\text{Nat}(h^C, F)\), where \(h^C = \mathrm{Hom}_\mathcal{C}(C, -)\). |
| Main Result | \(\mathrm{Hom}_\mathcal{D}(F(C), D) \cong \mathrm{Hom}_\mathcal{C}(C, G(D))\) natural in \(C\) and \(D\). | \(\mathrm{Nat}(h^C, F) \cong F(C)\) natural in \(C\) and \(F\). |
| Purpose | Construct adjoints to understand universal constructions and categorical limits/colimits. | Identify elements of functors and facilitate category embedding via representable functors. |
| Applications | Universal algebra, algebraic topology, and limits/colimits formulations. | Representability conditions, characterization of functors, model theory. |
| Seminal Authors | Samuel Eilenberg, Saunders Mac Lane (1945). | Nobuo Yoneda (1954). |
Introduction to Adjunctions and the Yoneda Lemma
Adjunctions establish a fundamental correspondence between pairs of functors, revealing an intrinsic relationship through natural transformations between hom-sets in category theory. The Yoneda Lemma provides a powerful tool connecting objects in a category to sets of natural transformations, allowing the embedding of any category into a functor category. Understanding adjunctions and the Yoneda Lemma facilitates deep insights into representable functors, universal properties, and the structural essence of categories in mathematical contexts.
Fundamental Concepts in Category Theory
Adjunctions in category theory represent a pair of functors connecting two categories, providing a universal mapping property that generalizes constructions such as free objects and limits. The Yoneda lemma characterizes a category's objects by embedding them into a functor category, revealing that every object is naturally isomorphic to the hom-functor it represents. Both the adjunction framework and the Yoneda lemma serve as foundational tools for understanding morphisms, functors, and natural transformations, highlighting the deep interplay between objects and their hom-sets in categorical contexts.
Defining Adjunctions: Basic Structure and Properties
Adjunctions are characterized by a pair of functors \(F : \mathcal{C} \to \mathcal{D}\) and \(G : \mathcal{D} \to \mathcal{C}\) along with natural transformations called the unit \(\eta: \text{id}_{\mathcal{C}} \to GF\) and counit \(\varepsilon: FG \to \text{id}_{\mathcal{D}}\) satisfying triangular identities. These structures establish a bijection between the hom-sets \(\text{Hom}_{\mathcal{D}}(F(c), d)\) and \(\text{Hom}_{\mathcal{C}}(c, G(d))\) natural in objects \(c \in \mathcal{C}\) and \(d \in \mathcal{D}\). The coherence conditions of the unit and counit enforce that \(F\) is left adjoint to \(G\), capturing the fundamental correspondence at the heart of adjunction theory.
Understanding the Yoneda Lemma: Statement and Significance
The Yoneda Lemma states that for any category C, an object X in C, and a functor F from C to Set, there is a natural isomorphism between the set of natural transformations from Hom_C(X, -) to F and the set F(X). This lemma plays a crucial role in category theory by embedding objects into a functor category, allowing complex structures to be studied via representable functors. Understanding the Yoneda Lemma enables deeper insights into adjunctions, natural transformations, and the foundational nature of categories.
Key Differences Between Adjunction and the Yoneda Lemma
Adjunction establishes a fundamental relationship between two functors, capturing how one functor is a left or right adjoint to another through natural isomorphisms of hom-sets. The Yoneda lemma, on the other hand, provides a natural isomorphism between a functor represented by an object and the set of natural transformations to that functor, focusing on embedding objects into presheaf categories. Key differences lie in their focus: adjunctions describe equivalences between hom-sets modulated by functors, while the Yoneda lemma emphasizes representability and fully faithful embeddings of categories into functor categories.
Applications of Adjunctions in Mathematics
Adjunctions play a crucial role in various fields of mathematics such as algebra, topology, and category theory by establishing a formal relationship between pairs of functors that preserve structure and reflect important properties. They enable the construction of free objects, the formulation of universal properties, and provide frameworks for understanding limits, colimits, and monads. These applications help simplify complex problems by translating them into adjoint pairs, facilitating deeper insights and essential abstractions in mathematical theory.
Applications of the Yoneda Lemma in Category Theory
The Yoneda Lemma is a fundamental tool in category theory that facilitates the embedding of any category into a presheaf category, enabling the analysis of objects via representable functors. This lemma plays a crucial role in defining natural transformations and equivalences between functors, providing a concrete method to study abstract categorical structures. Its applications include characterizing limits and colimits, representing objects up to isomorphism, and simplifying complex constructions within different categories.
Relationships and Interactions: Adjunctions and Yoneda Lemma
Adjunctions establish a fundamental correspondence between pairs of functors, encoding how one functor is naturally related to another through unit and counit transformations. The Yoneda lemma reveals the deep connection between an object and the natural transformations from representable functors, providing an isomorphism that characterizes presheaf categories. Together, adjunctions and the Yoneda lemma interact by showcasing how adjoint functors can be studied via representable functors and natural transformations, offering powerful tools for understanding categorical structures.
Comparative Examples: Adjunction vs. Yoneda Lemma
Adjunction in category theory describes a pair of functors exhibiting a natural isomorphism between hom-sets, enabling constructions like free and forgetful functors to be understood as universal approximations. The Yoneda lemma asserts that every functor to sets is naturally isomorphic to a hom-functor, providing a powerful tool to study objects via representable functors. Comparative examples highlight that while adjunctions frame relationships between different categories, the Yoneda lemma focuses internally on representing objects by their morphisms, making adjunctions global bridges and Yoneda local characterizations.
Conclusion: Insights and Practical Implications
The adjunction concept establishes a fundamental relationship between pairs of functors, revealing how constructions in one category can be systematically translated into another, while the Yoneda lemma provides a powerful tool for embedding any category into a presheaf category, enabling a deeper understanding of representable functors. Together, they offer critical insights for category theory, emphasizing the role of universal properties and natural transformations in structuring mathematical frameworks. These principles have practical implications in fields like algebraic geometry, functional programming, and type theory, where they enable precise modeling of mathematical objects and computational effects.
Adjunction Infographic
 libterm.com
libterm.com