A semiring is an algebraic structure consisting of two operations, typically addition and multiplication, that generalize the arithmetic of natural numbers while relaxing certain constraints like additive inverses. It finds applications in computer science, optimization, automata theory, and formal language processing due to its versatile properties. Explore the rest of this article to understand how semirings can enhance your approach to complex mathematical and computational problems.
Table of Comparison
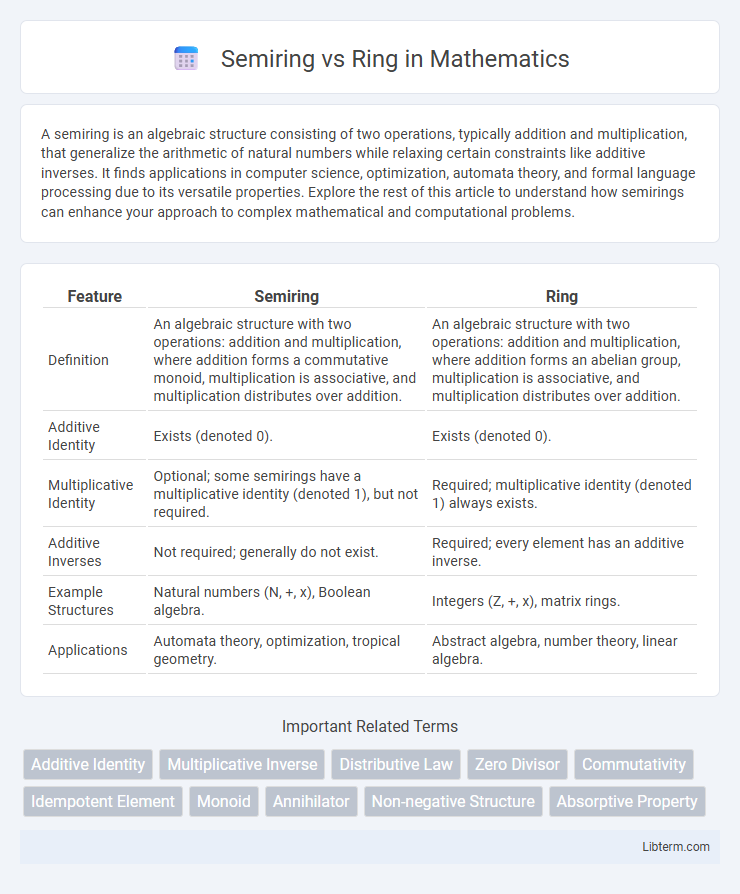
| Feature | Semiring | Ring |
|---|---|---|
| Definition | An algebraic structure with two operations: addition and multiplication, where addition forms a commutative monoid, multiplication is associative, and multiplication distributes over addition. | An algebraic structure with two operations: addition and multiplication, where addition forms an abelian group, multiplication is associative, and multiplication distributes over addition. |
| Additive Identity | Exists (denoted 0). | Exists (denoted 0). |
| Multiplicative Identity | Optional; some semirings have a multiplicative identity (denoted 1), but not required. | Required; multiplicative identity (denoted 1) always exists. |
| Additive Inverses | Not required; generally do not exist. | Required; every element has an additive inverse. |
| Example Structures | Natural numbers (N, +, x), Boolean algebra. | Integers (Z, +, x), matrix rings. |
| Applications | Automata theory, optimization, tropical geometry. | Abstract algebra, number theory, linear algebra. |
Introduction to Algebraic Structures
Semirings and rings are fundamental algebraic structures that differ primarily in the presence of additive inverses; rings require additive inverses for every element, while semirings do not. In a semiring, addition is commutative, associative, and has an identity element, but subtraction is generally not defined, which makes semirings suitable for applications like automata theory and optimization. Rings extend semirings by including additive inverses, enabling more complex operations such as solving linear equations in abstract algebra and number theory.
What is a Semiring?
A semiring is an algebraic structure consisting of a set equipped with two binary operations, typically called addition and multiplication, where addition is associative and commutative with an identity element, multiplication is associative with an identity, and multiplication distributes over addition. Unlike rings, semirings do not require additive inverses, meaning negative elements need not exist. Semirings are fundamental in areas such as automata theory, optimization, and formal language theory due to their relaxed structure compared to rings.
What is a Ring?
A ring is an algebraic structure consisting of a set equipped with two binary operations: addition and multiplication, where addition forms an abelian group and multiplication is associative with distributive laws linking the two operations. Unlike semirings, rings require additive inverses for every element, ensuring subtraction is always possible. Classic examples of rings include the set of integers, polynomials, and square matrices over a field, all fundamental in abstract algebra and number theory.
Key Differences Between Semiring and Ring
Semirings and rings differ primarily in the presence of additive inverses; rings require each element to have an additive inverse, while semirings do not. Rings possess subtraction operations due to this property, but semirings only support addition and multiplication without inverses, making them suitable for applications like automata theory and optimization. The distributive property holds in both structures, but semirings emphasize non-negative computations, contrasting with the more flexible algebraic structure of rings.
Axioms and Properties Comparison
A semiring is an algebraic structure consisting of a set equipped with two binary operations, addition and multiplication, where addition forms a commutative monoid with an identity element, multiplication forms a monoid with an identity element, multiplication distributes over addition, and the additive identity is multiplicatively absorbing. In contrast, a ring requires the additive structure to be an abelian group, meaning every element has an additive inverse, and multiplication is associative with distributivity over addition similar to semirings. Unlike rings, semirings do not require additive inverses, which impacts properties such as the existence of subtraction and negative elements in ring theory.
Examples of Semirings
Semirings are algebraic structures with two binary operations, typically addition and multiplication, where addition is commutative and associative with an identity element, and multiplication is associative with an identity, but subtraction may not be defined. Examples of semirings include the natural numbers (N, +, x), Boolean algebra (with OR as addition and AND as multiplication), and tropical semirings used in optimization and algebraic geometry. Unlike rings, semirings do not require additive inverses, making them suitable for applications in computer science, automata theory, and formal language theory.
Examples of Rings
Rings are algebraic structures consisting of a set equipped with two binary operations: addition and multiplication, where addition forms an abelian group and multiplication is associative. Common examples of rings include the set of integers \(\mathbb{Z}\), the set of \(n \times n\) matrices over a field, and polynomial rings like \(\mathbb{R}[x]\). Unlike semirings, rings require the existence of additive inverses, ensuring every element has a negative counterpart under addition.
Applications of Semirings
Semirings are widely used in computer science for pathfinding algorithms, like the shortest path in graphs using the tropical semiring, and in formal language theory for weighted automata. Their structure, which lacks additive inverses, makes them ideal for optimization problems and parsing in natural language processing where accumulation of weights or costs occurs. Unlike rings, semirings enable efficient modeling of systems with nonnegative quantities, such as probabilities and resource usage in dynamic programming.
Applications of Rings
Rings play a crucial role in algebraic structures applied extensively in cryptography, error-correcting codes, and polynomial factorization. The presence of additive inverses in rings enables the use of ring theory in solving linear equations, module theory, and algebraic geometry. Unlike semirings, rings support operations essential for Fourier analysis and number theory, making them fundamental in both theoretical and applied mathematics.
Choosing Between Semiring and Ring
Choosing between a semiring and a ring depends on the algebraic properties required for the application; rings include additive inverses enabling subtraction, while semirings lack this feature and thus are suitable for scenarios where negative elements are not defined or needed. Semirings find frequent use in computer science, optimization, and automata theory due to their closure under addition and multiplication without requiring additive inverses, whereas rings are preferred in algebra and number theory for their richer structure supporting subtraction and more complex operations. Evaluating the need for additive inverses and the complexity of operations guides the choice, with semirings offering simpler, more efficient models and rings enabling a full range of arithmetic manipulations.
Semiring Infographic
 libterm.com
libterm.com