Sequence refers to an ordered set of elements, often numbers or objects, arranged according to a specific rule or pattern. Understanding sequences is fundamental in mathematics, computer science, and various real-world applications such as data analysis and algorithm design. Explore the full article to discover how mastering sequences can enhance your problem-solving skills and analytical thinking.
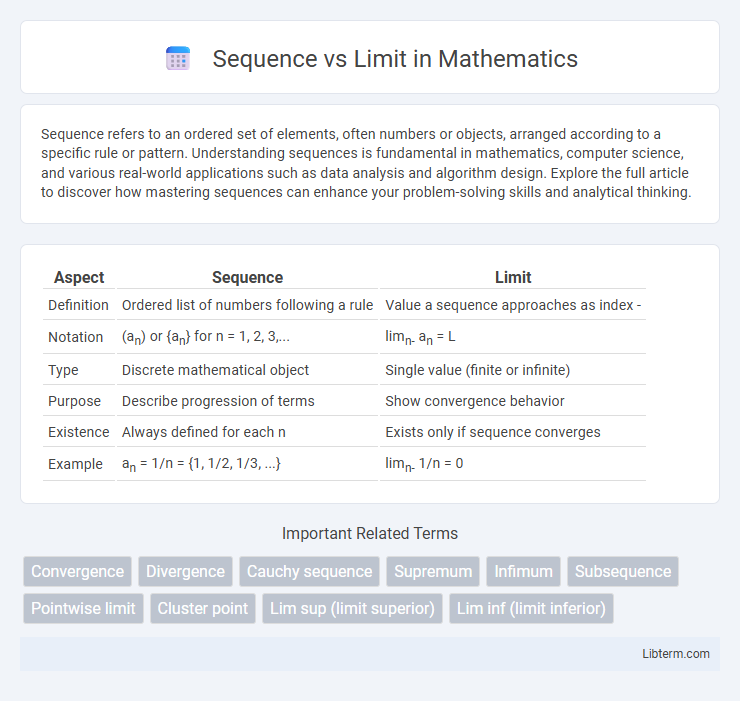
Table of Comparison
| Aspect | Sequence | Limit |
|---|---|---|
| Definition | Ordered list of numbers following a rule | Value a sequence approaches as index - |
| Notation | (an) or {an} for n = 1, 2, 3,... | limn- an = L |
| Type | Discrete mathematical object | Single value (finite or infinite) |
| Purpose | Describe progression of terms | Show convergence behavior |
| Existence | Always defined for each n | Exists only if sequence converges |
| Example | an = 1/n = {1, 1/2, 1/3, ...} | limn- 1/n = 0 |
Introduction to Sequence and Limit
A sequence is an ordered list of numbers defined by a specific rule or function, where each term corresponds to an index usually represented by natural numbers. The limit of a sequence refers to the value that the terms of the sequence approach as the index increases indefinitely. Understanding the concept of limits is fundamental in analyzing the behavior and convergence of sequences in mathematical analysis.
Understanding Mathematical Sequences
Mathematical sequences are ordered lists of numbers following a specific pattern, where each term depends on its position or previous terms. The concept of a limit describes the value that the terms of a sequence approach as the index goes to infinity, providing insight into the sequence's long-term behavior. Understanding the distinction between a sequence and its limit is essential for analyzing convergence and divergence in calculus and real analysis.
Defining Limits in Mathematics
A limit in mathematics defines the value that a sequence approaches as the index grows indefinitely, capturing the behavior of terms near infinity. Sequences are ordered lists of numbers, and understanding their limits is crucial for analyzing continuity, derivatives, and integrals in calculus. The formal definition of a limit uses the epsilon-delta criterion to precisely describe how sequence terms get arbitrarily close to a specific value.
Key Differences Between Sequence and Limit
A sequence is an ordered list of numbers defined by a specific rule or formula, while a limit describes the value that the elements of a sequence approach as the index approaches infinity. Sequences can be finite or infinite, characterized by their terms, whereas limits provide a precise mathematical concept representing the behavior of a sequence at its boundary. The key difference lies in the sequence being a set of values, and the limit being the eventual value those terms converge to or diverge from.
Importance of Sequences in Calculus
Sequences play a fundamental role in calculus by providing a framework to analyze the behavior of functions and their limits. Understanding the convergence or divergence of sequences is essential for defining limits rigorously and for developing concepts such as continuity, derivatives, and integrals. The study of sequences enables mathematicians to approximate complex functions and solve problems related to infinite processes and series.
Role of Limits in Analyzing Sequences
Limits play a crucial role in analyzing sequences by determining the value a sequence approaches as the index grows indefinitely. Understanding the limit of a sequence helps in classifying sequences as convergent or divergent, which is fundamental in calculus and mathematical analysis. This concept enables the precise description of long-term behavior of sequences, aiding in problem-solving and theoretical proofs.
Common Types of Sequences and Their Limits
Arithmetic sequences have a constant difference between consecutive terms, and their limits tend to infinity or negative infinity unless the difference is zero, making the sequence constant. Geometric sequences multiply each term by a fixed ratio, converging to zero if the absolute value of the ratio is less than one, or diverging otherwise. Harmonic sequences, defined as the reciprocal of natural numbers, approach zero as their limit, demonstrating a slowly converging behavior.
Real-World Applications of Sequence and Limit
In engineering, sequences model discrete data points over time, such as temperature readings, while limits predict steady-state behaviors critical for system stability analysis. In finance, limits help determine the long-term value of investment sequences, guiding decisions on asset growth and risk assessment. Control systems rely on limits to ensure outputs approach desired values despite varying inputs, enhancing automation precision and reliability.
Common Mistakes: Sequence vs Limit
Confusing a sequence with its limit is a common mistake, as sequences are lists of numbers defined by a specific rule, while a limit is the value the sequence approaches as the index goes to infinity. Another frequent error is assuming that all sequences have limits, ignoring that some sequences diverge or oscillate indefinitely. Misunderstanding the distinction between the value of a sequence's term and the limit can lead to incorrect conclusions in calculus and analysis problems.
Summary and Key Takeaways
A sequence is an ordered list of numbers following a specific pattern, while a limit describes the value that the terms of a sequence approach as the index goes to infinity. Understanding limits is essential for analyzing sequence behavior, convergence, and divergence. Key takeaways include recognizing that a sequence converges if its limit exists and diverges if the limit does not exist or is infinite.
Sequence Infographic
 libterm.com
libterm.com