Polar decomposition breaks down any square matrix into a product of a unitary matrix and a positive-semidefinite Hermitian matrix, revealing intrinsic properties of linear transformations. This method is essential in fields such as quantum mechanics, computer graphics, and numerical analysis for understanding matrix behavior and stability. Explore further to understand how polar decomposition can simplify complex problems in your work or studies.
Table of Comparison
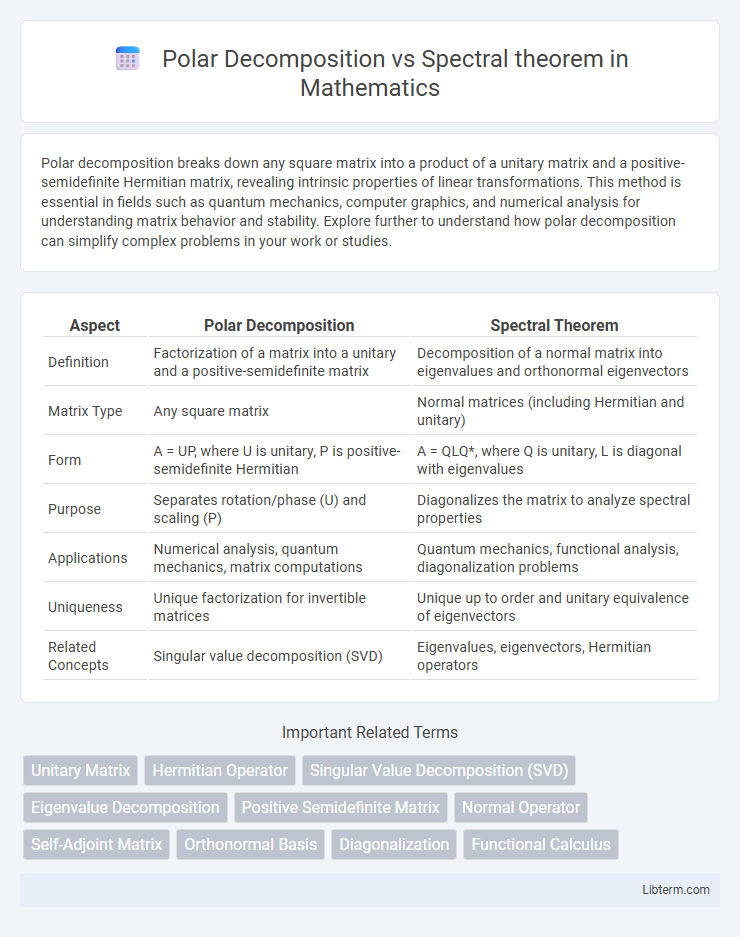
| Aspect | Polar Decomposition | Spectral Theorem |
|---|---|---|
| Definition | Factorization of a matrix into a unitary and a positive-semidefinite matrix | Decomposition of a normal matrix into eigenvalues and orthonormal eigenvectors |
| Matrix Type | Any square matrix | Normal matrices (including Hermitian and unitary) |
| Form | A = UP, where U is unitary, P is positive-semidefinite Hermitian | A = QLQ*, where Q is unitary, L is diagonal with eigenvalues |
| Purpose | Separates rotation/phase (U) and scaling (P) | Diagonalizes the matrix to analyze spectral properties |
| Applications | Numerical analysis, quantum mechanics, matrix computations | Quantum mechanics, functional analysis, diagonalization problems |
| Uniqueness | Unique factorization for invertible matrices | Unique up to order and unitary equivalence of eigenvectors |
| Related Concepts | Singular value decomposition (SVD) | Eigenvalues, eigenvectors, Hermitian operators |
Introduction to Polar Decomposition and Spectral Theorem
Polar decomposition expresses any square matrix as the product of a unitary matrix and a positive-semidefinite Hermitian matrix, providing a geometric interpretation of linear transformations. The spectral theorem characterizes normal matrices by diagonalizing them through a unitary basis related to their eigenvalues, revealing essential spectral properties. Both concepts are fundamental in linear algebra and functional analysis, playing crucial roles in operator theory and matrix factorization techniques.
Fundamental Concepts in Linear Algebra
Polar decomposition expresses any square matrix as the product of a unitary matrix and a positive semi-definite Hermitian matrix, emphasizing matrix factorization into rotational and scaling parts. The spectral theorem applies to normal matrices, guaranteeing diagonalization via a unitary matrix with real eigenvalues, highlighting the matrix's orthonormal eigenbasis representation. Both concepts reveal underlying structure in linear operators, with polar decomposition focusing on geometric interpretation and the spectral theorem emphasizing eigenvalue-eigenvector analysis.
Definition and Mathematical Formulation of Polar Decomposition
Polar decomposition expresses any complex square matrix A as the product of a unitary matrix U and a positive semi-definite Hermitian matrix P, formulated as A = UP. The matrix P is uniquely defined as the positive square root of A*A, where A* is the conjugate transpose of A, ensuring P = (A*A)^(1/2). This decomposition contrasts with the spectral theorem, which diagonalizes normal matrices through unitary similarity transformations, emphasizing eigenvalues and eigenvectors rather than a factorization into unitary and positive components.
Definition and Mathematical Formulation of Spectral Theorem
The Spectral Theorem states that any normal operator on a finite-dimensional complex inner product space can be diagonalized by a unitary matrix, meaning it can be expressed as \( A = U \Lambda U^* \), where \( U \) is unitary and \( \Lambda \) is a diagonal matrix containing eigenvalues. In contrast, Polar Decomposition factorizes a matrix \( A \) as \( A = UP \), where \( U \) is unitary and \( P \) is positive semidefinite Hermitian, emphasizing different structural insights. The Spectral Theorem's mathematical formulation directly relates to eigenvalue decomposition, providing powerful tools for analyzing normal matrices via spectral properties.
Matrix Types: Applicability of Polar Decomposition and Spectral Theorem
Polar Decomposition applies to any square matrix, decomposing it into a unitary matrix and a positive semidefinite matrix, making it versatile for general complex matrices. The Spectral Theorem is specifically applicable to normal matrices, including Hermitian and unitary matrices, where it guarantees diagonalization via a unitary basis. While Polar Decomposition handles broader matrix classes, the Spectral Theorem provides more detailed spectral information but requires stricter matrix conditions.
Computational Methods and Algorithms
Polar decomposition and the spectral theorem both provide matrix factorization frameworks but differ in computational methods and algorithms. Polar decomposition typically utilizes iterative algorithms like the Newton method or singular value decomposition (SVD) to express a matrix as the product of a unitary and positive-semidefinite matrix, optimizing numerical stability for rectangular or non-Hermitian matrices. The spectral theorem applies primarily to normal matrices, solving eigenvalue problems through unitary diagonalization algorithms such as QR iteration or divide-and-conquer approaches, focusing on eigenvalue and eigenvector computations crucial for quantum mechanics and vibration analysis.
Geometric Interpretation and Physical Meaning
Polar decomposition expresses a matrix as the product of a unitary (or orthogonal) matrix and a positive semi-definite matrix, representing a rotation followed by a scaling transformation, which geometrically separates shape distortion from orientation. The spectral theorem decomposes a normal matrix into orthonormal eigenvectors and real eigenvalues, offering a geometric interpretation where the matrix acts by stretching space along mutually perpendicular axes. Physically, polar decomposition aligns closely with rigid body motions and deformation analysis, while the spectral theorem is fundamental in vibration modes and quantum mechanics for understanding energy levels and state projections.
Key Differences: Polar Decomposition vs Spectral Theorem
Polar decomposition and the spectral theorem both factorize matrices but serve different purposes and apply under different conditions. Polar decomposition expresses any square matrix as the product of a unitary matrix and a positive-semidefinite matrix, emphasizing geometric interpretations. The spectral theorem applies primarily to normal matrices, decomposing them into orthonormal eigenvectors and diagonal eigenvalue matrices, highlighting spectral properties and eigenvalue analysis.
Practical Applications in Science and Engineering
Polar decomposition provides a powerful tool for matrix factorization in computer graphics and robotics, enabling the separation of rotational and scaling components for motion analysis and simulation. The spectral theorem's diagonalization of symmetric matrices plays a critical role in vibration analysis, quantum mechanics, and structural engineering by simplifying eigenvalue problems and facilitating stability assessments. Both decompositions optimize computational efficiency and accuracy in solving linear systems and modeling complex physical phenomena.
Conclusion: Choosing Between Polar Decomposition and Spectral Theorem
Polar Decomposition provides a unique factorization of any square matrix into a unitary and a positive-semidefinite matrix, making it highly effective for analyzing matrix norms and stability in complex systems. The Spectral Theorem excels in diagonalizing normal matrices, offering clear insight into eigenvalues and eigenvectors, which is essential in quantum mechanics and vibration analysis. Selecting between these methods depends on the matrix properties and application goals: use Polar Decomposition for stability and norm-related problems, and the Spectral Theorem for eigenvalue decomposition of normal operators.
Polar Decomposition Infographic
 libterm.com
libterm.com