Counting measure assigns a value to each subset of a given set equal to the number of elements contained within it, providing a straightforward way to quantify discrete collections. It plays a fundamental role in measure theory, particularly in contexts involving finite or countable sets, where it simplifies integration and probability calculations. Explore the rest of the article to understand how counting measure applies across diverse mathematical and applied fields.
Table of Comparison
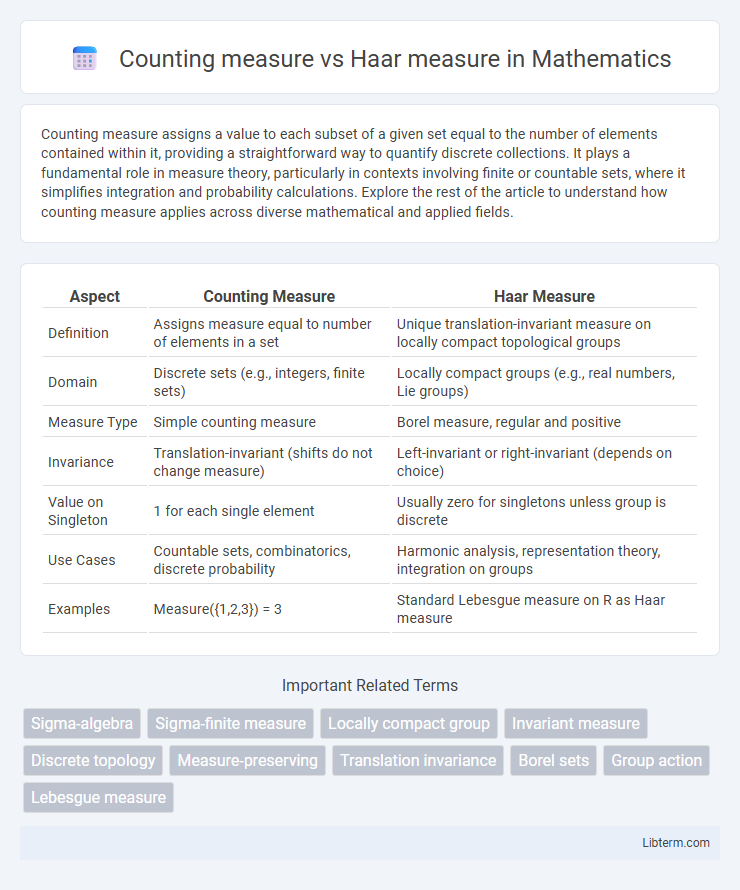
| Aspect | Counting Measure | Haar Measure |
|---|---|---|
| Definition | Assigns measure equal to number of elements in a set | Unique translation-invariant measure on locally compact topological groups |
| Domain | Discrete sets (e.g., integers, finite sets) | Locally compact groups (e.g., real numbers, Lie groups) |
| Measure Type | Simple counting measure | Borel measure, regular and positive |
| Invariance | Translation-invariant (shifts do not change measure) | Left-invariant or right-invariant (depends on choice) |
| Value on Singleton | 1 for each single element | Usually zero for singletons unless group is discrete |
| Use Cases | Countable sets, combinatorics, discrete probability | Harmonic analysis, representation theory, integration on groups |
| Examples | Measure({1,2,3}) = 3 | Standard Lebesgue measure on R as Haar measure |
Introduction to Counting Measure and Haar Measure
Counting measure assigns a value equal to the number of elements in a set, making it ideal for discrete spaces where each individual element contributes a unit measure. Haar measure extends this concept to locally compact topological groups, providing a unique, translation-invariant measure that generalizes the notion of length, area, or volume. While counting measure is straightforward and atomic, Haar measure captures continuous symmetries and is fundamental in harmonic analysis and representation theory.
Definitions: Counting Measure Explained
Counting measure assigns a value equal to the number of elements in a given set, making it a simple yet fundamental example of a measure on discrete spaces. It maps every finite subset of a space to its cardinality and every infinite subset to infinity, providing a straightforward way to quantify size. In contrast, Haar measure is defined on locally compact topological groups and generalizes the concept of volume, remaining invariant under group translations.
Understanding the Haar Measure
The Haar measure is a unique, translation-invariant measure defined on locally compact topological groups, allowing integration that respects the group's structure. Unlike the counting measure, which assigns a measure of one to each singleton set and is naturally discrete, the Haar measure generalizes volume in continuous groups such as Lie groups or real numbers, providing a foundation for harmonic analysis. This measure enables meaningful integration on groups, supporting applications in representation theory, probability, and differential geometry.
Key Differences between Counting and Haar Measures
Counting measure assigns a measure equal to the cardinality of a set, making it discrete and purely atomic, while Haar measure is a translation-invariant measure defined on locally compact topological groups, often non-atomic and continuous. The counting measure is suitable for countable sets without topology, whereas Haar measure incorporates group structure and topology, providing invariance under group actions, crucial in harmonic analysis and representation theory. Unlike counting measure, Haar measure can be normalized to be finite on compact groups but infinite on non-compact groups, reflecting key differences in measure theory and functional analysis applications.
Mathematical Properties of Counting Measure
Counting measure assigns to each set the number of elements within it, making it a discrete measure primarily defined on countable spaces. It is sigma-finite as every singleton has finite measure equal to one, facilitating straightforward integration of simple functions. Unlike Haar measure, which is translation-invariant on locally compact groups, counting measure lacks general invariance properties but is uniquely suited for discrete spaces due to its natural alignment with set cardinality.
Properties and Uniqueness of Haar Measure
The counting measure assigns a measure equal to the number of points in a set, operating on discrete spaces and lacking invariance under group actions beyond trivial cases. Haar measure, defined on locally compact topological groups, is unique up to scaling and invariant under group translations, providing a fundamental tool for harmonic analysis and representation theory. Its existence and uniqueness, proven by Haar's theorem, ensure a consistent way to integrate functions over groups with rich topological structure, unlike the counting measure which is generally not applicable in continuous settings.
Applications in Measure Theory
Counting measure assigns a measure equal to the number of elements in a set, making it ideal for discrete spaces and combinatorial problems where cardinality is central. Haar measure, defined on locally compact topological groups, provides a translation-invariant way to measure subsets, essential for harmonic analysis, representation theory, and probability on groups. In measure theory applications, counting measure simplifies integration over countable sets, while Haar measure generalizes integration on continuous groups, enabling advanced studies in ergodic theory and abstract harmonic analysis.
Examples: Counting Measure vs Haar Measure
Counting measure assigns a measure of one to each individual element in a set, making it ideal for discrete spaces like the integers Z, where each point is measured uniquely. Haar measure generalizes this concept for locally compact topological groups, such as the circle group S^1 or the real numbers R, providing an invariant measure that respects the group structure and enables integration over continuous groups. For example, on Z, the counting measure counts elements, while on R, the Haar measure coincides with the Lebesgue measure, invariant under translations.
Importance in Abstract Harmonic Analysis
Counting measure assigns a fixed weight of one to each point in a discrete group, making it essential for analyzing sums and series in abstract harmonic analysis on countable sets. Haar measure, uniquely defined on locally compact topological groups, provides a translation-invariant measure enabling integration and Fourier analysis on continuous groups. These measures facilitate the study of representations, convolution operators, and harmonic decomposition by allowing seamless transition between discrete and continuous group frameworks.
Summary: Choosing the Right Measure
Counting measure assigns a value based on the number of elements in a set, ideal for discrete spaces where each singleton has measure one. Haar measure generalizes this concept to locally compact groups, providing an invariant measure under group operations, essential for continuous structures like Lie groups or topological groups. Selecting between counting and Haar measure depends on the algebraic and topological properties of the space, ensuring the measure aligns with the space's discrete or continuous nature.
Counting measure Infographic
 libterm.com
libterm.com