Span refers to the length or distance between two points, commonly used in architecture and engineering to describe the horizontal extent of a structure. Understanding span is crucial when assessing load distribution and ensuring the stability of bridges, beams, or roofs. Dive deeper into the article to explore how span impacts design choices and material selection.
Table of Comparison
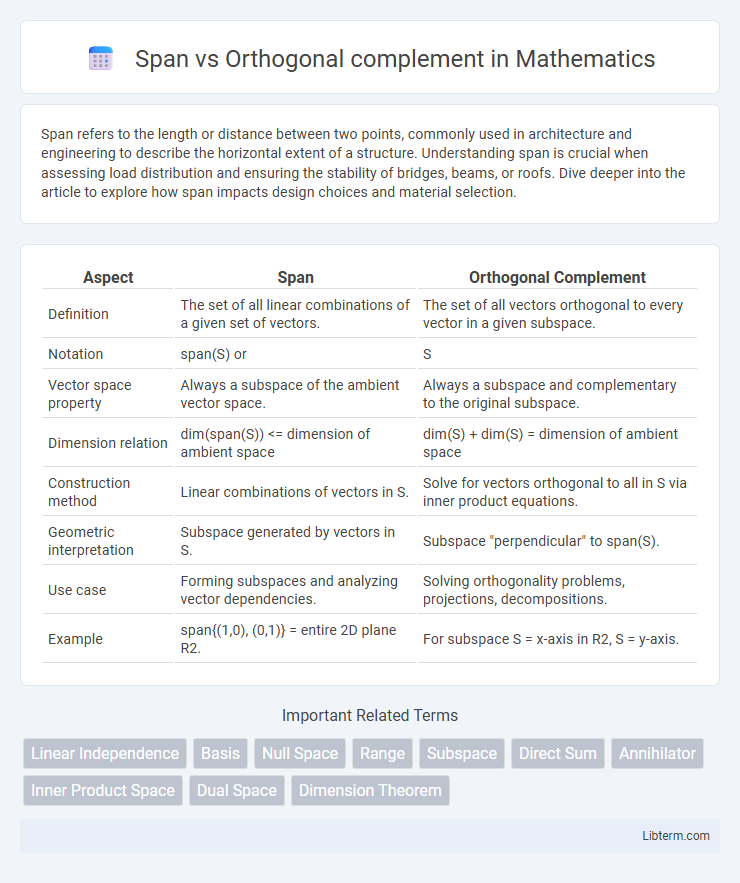
| Aspect | Span | Orthogonal Complement |
|---|---|---|
| Definition | The set of all linear combinations of a given set of vectors. | The set of all vectors orthogonal to every vector in a given subspace. |
| Notation | span(S) or |
S |
| Vector space property | Always a subspace of the ambient vector space. | Always a subspace and complementary to the original subspace. |
| Dimension relation | dim(span(S)) <= dimension of ambient space | dim(S) + dim(S) = dimension of ambient space |
| Construction method | Linear combinations of vectors in S. | Solve for vectors orthogonal to all in S via inner product equations. |
| Geometric interpretation | Subspace generated by vectors in S. | Subspace "perpendicular" to span(S). |
| Use case | Forming subspaces and analyzing vector dependencies. | Solving orthogonality problems, projections, decompositions. |
| Example | span{(1,0), (0,1)} = entire 2D plane R2. | For subspace S = x-axis in R2, S = y-axis. |
Introduction to Span and Orthogonal Complement
The span of a set of vectors in a vector space is the collection of all possible linear combinations of those vectors, forming a subspace that captures every direction represented by the original vectors. The orthogonal complement of a subspace consists of all vectors that are orthogonal to every vector in that subspace, providing a powerful tool for decomposing vectors and solving linear equations. Understanding both span and orthogonal complements is fundamental in linear algebra for characterizing subspaces and analyzing vector relationships.
Definition of Vector Space Span
The span of a set of vectors in a vector space is defined as the collection of all possible linear combinations of those vectors, forming the smallest subspace containing them. The orthogonal complement of a subspace consists of all vectors in the ambient vector space that are orthogonal to every vector in the subspace, creating a direct sum decomposition when combined with the original subspace. Understanding the span is fundamental for constructing vector spaces, as it helps identify all vectors reachable through linear combination, while the orthogonal complement provides insight into the structure and dimensionality of the space.
Understanding Orthogonal Complements
The orthogonal complement of a subspace consists of all vectors that are perpendicular to every vector in the given subspace, forming a key concept in linear algebra. Understanding orthogonal complements allows for the decomposition of vector spaces into direct sums, where any vector can be uniquely expressed as a sum of components from the subspace and its orthogonal complement. This concept is crucial in solving linear systems, analyzing projections, and optimizing vector space operations.
Geometric Interpretation of Span
The geometric interpretation of span refers to the collection of all possible linear combinations of a given set of vectors, forming a subspace such as a line, plane, or higher-dimensional space depending on the vectors involved. The orthogonal complement consists of all vectors that are perpendicular to every vector in the span, representing a subspace orthogonal to the original set. Understanding the span helps visualize how vectors generate space, while the orthogonal complement identifies directions independent from that span in Euclidean space.
Geometric Interpretation of Orthogonal Complements
The orthogonal complement of a subspace consists of all vectors perpendicular to every vector in the original subspace, forming a geometric space that captures directions independent from the span. While the span represents all linear combinations of given vectors, the orthogonal complement highlights the geometric notion of all vectors orthogonal to that span in the ambient space. This duality enables decomposition of any vector into components aligned with the subspace and components perpendicular to it, reflecting a fundamental geometric structure in vector spaces.
Mathematical Properties of Span
The span of a set of vectors in a vector space is the collection of all possible linear combinations of those vectors, forming a subspace characterized by closure under vector addition and scalar multiplication. Its dimension equals the number of linearly independent vectors in the set, directly influencing the rank of the vector space. Unlike the orthogonal complement, which contains all vectors orthogonal to a given subspace, the span defines the minimal subspace enclosing the original vectors, crucial for understanding bases and linear independence in linear algebra.
Key Properties of Orthogonal Complements
The orthogonal complement of a subspace in an inner product space consists of all vectors orthogonal to every vector in that subspace, ensuring the intersection between the subspace and its orthogonal complement contains only the zero vector. Key properties include the fact that the orthogonal complement is itself a subspace, and the direct sum of a subspace and its orthogonal complement spans the entire vector space. Furthermore, the dimension of a subspace plus the dimension of its orthogonal complement equals the dimension of the whole vector space, highlighting a fundamental relationship between the two.
Span vs Orthogonal Complement: Core Differences
Span refers to the set of all possible linear combinations of a given set of vectors in a vector space, representing the subspace they generate. The orthogonal complement consists of all vectors in the vector space that are perpendicular to every vector in the original subspace, forming a distinct subspace. The core difference lies in their construction: the span builds from linear combinations inside the space, while the orthogonal complement contains vectors that have zero inner product with the span's vectors.
Applications in Linear Algebra and Data Science
Span defines the set of all linear combinations of a given vector set, essential for determining vector space coverage and basis construction in linear algebra. The orthogonal complement consists of all vectors orthogonal to a subspace, crucial for solving projection problems, optimization, and orthogonal decomposition techniques. In data science, span helps in feature space representation and dimensionality reduction, while orthogonal complements underpin principal component analysis and error minimization in regression models.
Summary and Practical Implications
The span of a set of vectors defines all possible linear combinations within a vector space, representing the entire subspace these vectors generate. The orthogonal complement consists of all vectors orthogonal to every vector in the span, serving as a critical tool in decomposition and projection problems. Understanding the relationship aids in solving linear systems, optimizing algorithms in signal processing, and performing dimensionality reduction in machine learning.
Span Infographic
 libterm.com
libterm.com