A comeager set, in topology, is a subset of a topological space whose complement is meager, meaning it is the countable union of nowhere dense sets. These sets are considered "large" in the sense of Baire category, often implying they are dense and prevalent within the space. Discover how comeager sets influence topological properties and their applications by reading the rest of the article.
Table of Comparison
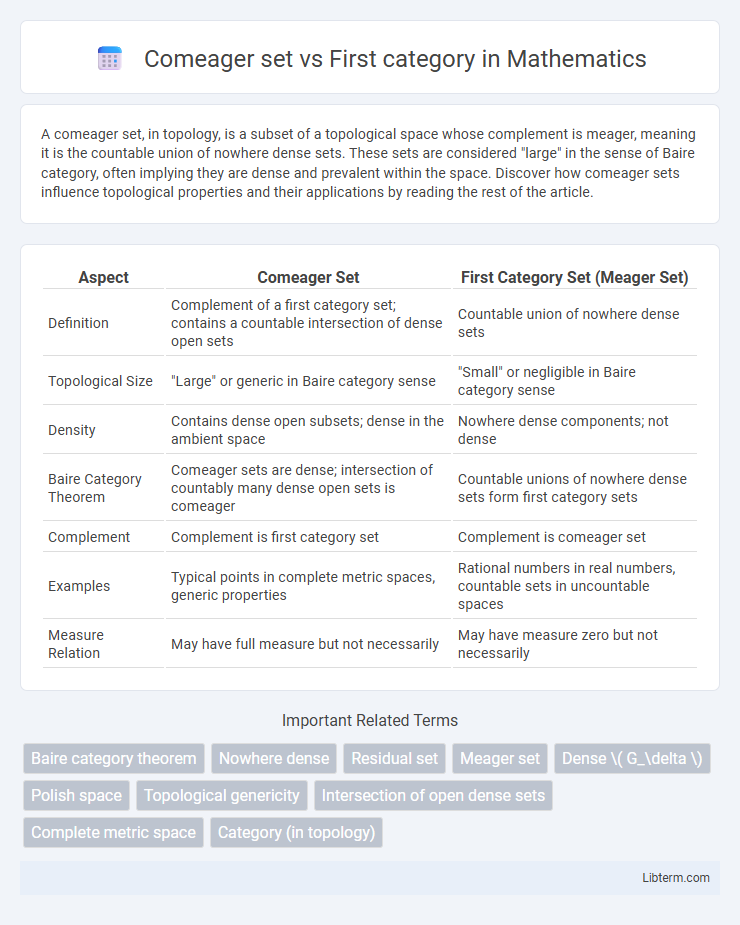
| Aspect | Comeager Set | First Category Set (Meager Set) |
|---|---|---|
| Definition | Complement of a first category set; contains a countable intersection of dense open sets | Countable union of nowhere dense sets |
| Topological Size | "Large" or generic in Baire category sense | "Small" or negligible in Baire category sense |
| Density | Contains dense open subsets; dense in the ambient space | Nowhere dense components; not dense |
| Baire Category Theorem | Comeager sets are dense; intersection of countably many dense open sets is comeager | Countable unions of nowhere dense sets form first category sets |
| Complement | Complement is first category set | Complement is comeager set |
| Examples | Typical points in complete metric spaces, generic properties | Rational numbers in real numbers, countable sets in uncountable spaces |
| Measure Relation | May have full measure but not necessarily | May have measure zero but not necessarily |
Introduction to Comeager Sets and First Category
Comeager sets, also known as sets of second category, are dense subsets in a complete metric space whose complements are meager or of first category. First category sets are countable unions of nowhere dense sets, meaning they are topologically small or negligible. Understanding the distinction between comeager sets and first category sets is fundamental in descriptive set theory and Baire category theorem applications.
Historical Context and Origins
The concepts of comeager sets and first category sets originated in early 20th-century descriptive set theory, particularly through the work of Rene-Louis Baire. Baire's category theorem, formulated in 1899, introduced these notions to classify subsets of complete metric spaces based on their topological "size" rather than measure. This foundational framework distinguished comeager sets as "large" or dense, while first category sets represented "small" or meager collections, shaping modern topology and functional analysis.
Definitions: Comeager Sets Explained
Comeager sets, also known as residual sets, are defined as the complements of first category sets within a topological space, meaning they contain a countable intersection of dense open sets. First category sets, or meager sets, are characterized as countable unions of nowhere dense sets, which possess empty interior and do not affect the overall density of the space. The distinction hinges on topological largeness: comeager sets are "large" and dense in the Baire category sense, while first category sets are considered "small" or negligible.
Definitions: First Category Sets Clarified
First category sets, also known as meager sets, are subsets of a topological space formed by a countable union of nowhere dense sets, meaning each component has empty interior. Comeager sets, in contrast, are complements of first category sets, representing a large or "generic" subset that is dense and contains a countable intersection of open dense sets. Understanding first category sets is crucial for analyzing Baire spaces, where every comeager set is dense and typical properties hold outside a meager exceptional set.
Key Differences Between Comeager and First Category
Comeager sets, also known as residual sets, are characterized by containing a countable intersection of dense open sets in a topological space, making them "large" or generic. First category sets (meager sets) are formed as a countable union of nowhere dense sets, signifying "smallness" or rarity in the space. The key difference lies in their topological density properties: comeager sets are dense and robust under countable intersections, while first category sets are topologically sparse and negligible.
Properties of Comeager Sets
Comeager sets, also known as residual sets, are dense in a complete metric space and can be expressed as the countable intersection of open dense sets, highlighting their prevalence in topological spaces. They possess the property of being large in the sense of Baire category, contrasting with sets of the first category, which are meager and can be covered by countably many nowhere dense sets. The intersection of countably many comeager sets remains comeager, ensuring stability under countable intersections and emphasizing their significance in descriptive set theory and functional analysis.
Properties of First Category Sets
First category sets, also known as meager sets, are countable unions of nowhere dense subsets in a topological space, exhibiting a topological smallness despite possibly being dense. These sets lack interior points and their complement, comeager sets, form residual sets that are large in the sense of Baire category. Properties of first category sets include being closed under countable unions but not under countable intersections, emphasizing their role as negligible or "small" in Baire category theory.
Examples in Topological Spaces
In topological spaces, a comeager set is a countable intersection of dense open sets, often exemplified by the set of irrational numbers in the real line, which is comeager in \( \mathbb{R} \). In contrast, a first category set (or meager set) is a countable union of nowhere dense sets, such as the rational numbers in \( \mathbb{R} \), which are topologically small despite being dense. These concepts illustrate the Baire category theorem, which states that in a complete metric space, comeager sets are large in the sense of category, while first category sets are considered negligible or sparse.
Applications in Real Analysis and Topology
Comeager sets, characterized by their countable intersection of dense open sets, play a crucial role in the Baire category theorem within real analysis and topology. First category sets, also known as meager sets, are unions of countably many nowhere dense sets, often regarded as "small" or negligible in topological spaces. Applications include proving generic properties in function spaces, where comeager sets represent typical behaviors, while first category sets identify exceptional or pathological cases in continuity, differentiability, and space structure analysis.
Summary: Comparing Comeager and First Category Sets
Comeager sets, also known as residual sets, are those whose complement is of the first category, meaning they are large or "typical" in the sense of Baire category theory. First category sets, or meager sets, are countable unions of nowhere dense sets and are considered "small" or negligible within a topological space. The key distinction lies in size and typicality: comeager sets are dense and prevalent, while first category sets are sparse and topologically insignificant.
Comeager set Infographic
 libterm.com
libterm.com