Fuzzy logic enhances decision-making by handling imprecise or uncertain information, mimicking human reasoning more closely than traditional binary systems. This approach is widely used in control systems, natural language processing, and artificial intelligence to improve adaptability and performance. Discover how fuzzy logic can optimize your systems by exploring the detailed insights in the rest of this article.
Table of Comparison
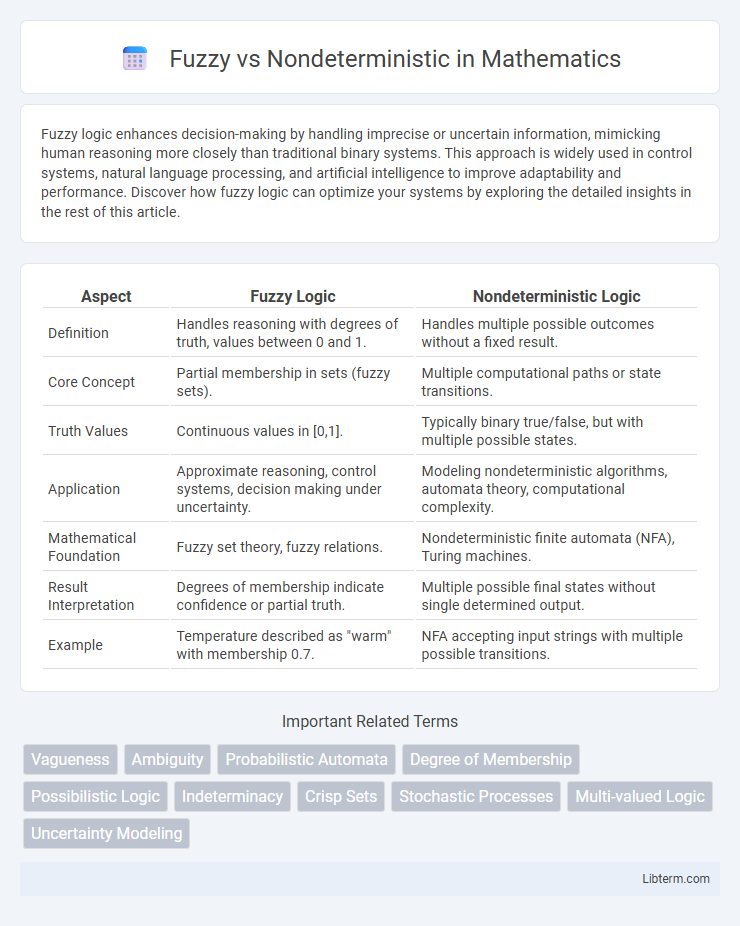
| Aspect | Fuzzy Logic | Nondeterministic Logic |
|---|---|---|
| Definition | Handles reasoning with degrees of truth, values between 0 and 1. | Handles multiple possible outcomes without a fixed result. |
| Core Concept | Partial membership in sets (fuzzy sets). | Multiple computational paths or state transitions. |
| Truth Values | Continuous values in [0,1]. | Typically binary true/false, but with multiple possible states. |
| Application | Approximate reasoning, control systems, decision making under uncertainty. | Modeling nondeterministic algorithms, automata theory, computational complexity. |
| Mathematical Foundation | Fuzzy set theory, fuzzy relations. | Nondeterministic finite automata (NFA), Turing machines. |
| Result Interpretation | Degrees of membership indicate confidence or partial truth. | Multiple possible final states without single determined output. |
| Example | Temperature described as "warm" with membership 0.7. | NFA accepting input strings with multiple possible transitions. |
Understanding Fuzzy Logic: An Overview
Fuzzy logic extends classical Boolean logic by allowing variables to have truth values ranging between 0 and 1, enabling more nuanced reasoning in systems with uncertainty or imprecise information. Unlike nondeterministic models that represent multiple possible outcomes without assigning degrees of certainty, fuzzy logic quantifies the degree of membership in fuzzy sets, improving decision-making processes in areas like control systems and artificial intelligence. The core advantage of fuzzy logic lies in its capability to mimic human reasoning by handling partial truths, thereby enhancing interpretability and flexibility compared to traditional nondeterministic approaches.
What is Nondeterminism? Key Concepts Explained
Nondeterminism refers to computational processes where multiple outcomes or states are possible from a single input, without a predetermined sequence, commonly modeled by nondeterministic finite automata (NFA). Key concepts include the ability to transition to several possible next states simultaneously and the lack of a fixed rule for choosing a single path, enabling exploration of all potential solutions in parallel. This contrasts with fuzzy logic, which deals with degrees of truth or membership values rather than multiple simultaneous states.
Fundamental Differences Between Fuzzy and Nondeterministic Systems
Fuzzy systems handle uncertainty by assigning degrees of membership to elements, enabling partial truths between completely true and false, while nondeterministic systems explore multiple possible outcomes without specific probabilities. Fuzzy logic works with continuous truth values ranging from 0 to 1, contrasting with nondeterministic models that rely on discrete states and transitions without determined outcomes. The key difference lies in fuzzy systems quantifying vagueness for approximate reasoning, whereas nondeterministic systems represent choices among several potential future states without inherent likelihoods.
Core Applications of Fuzzy Logic
Fuzzy logic excels in handling imprecise and uncertain data, making it ideal for applications such as control systems, decision-making processes, and pattern recognition. Unlike nondeterministic models that explore multiple possible outcomes, fuzzy logic provides graded reasoning, enabling more nuanced control in robotics, automotive systems, and consumer electronics. Core applications include adaptive control systems in washing machines, air conditioners, and medical diagnosis tools where crisp boundaries are inadequate.
Real-World Use Cases for Nondeterministic Approaches
Nondeterministic approaches excel in real-world applications such as concurrent system modeling, where multiple possible outcomes must be analyzed simultaneously to ensure system reliability and performance. In optimization problems, nondeterministic algorithms efficiently explore numerous solution paths to find optimal or near-optimal outcomes in fields like logistics and scheduling. Natural language processing also leverages nondeterminism to handle ambiguity and multiple interpretations, improving machine understanding and translation accuracy.
Decision-Making: Fuzzy vs. Nondeterministic Models
Fuzzy decision-making models handle uncertainty by assigning degrees of membership to possible outcomes, enabling more flexible and realistic reasoning in complex scenarios. Nondeterministic models, in contrast, represent uncertainty through multiple possible discrete states without probabilistic weights, reflecting scenarios where outcomes are not precisely predictable. The choice between fuzzy and nondeterministic models depends on whether gradual uncertainty or distinct multiple possibilities better captures the problem's decision-making landscape.
Mathematical Foundations: Fuzziness and Nondeterminism
Fuzziness is grounded in fuzzy set theory, which extends classical set theory by allowing elements to have degrees of membership characterized by values between 0 and 1, enabling the modeling of uncertainty and partial truth in mathematical logic. Nondeterminism, rooted in automata theory and formal language theory, involves systems where multiple possible transitions or states can arise from a single configuration, capturing ambiguity in computational processes. Both concepts address uncertainty but through distinct mathematical frameworks: fuzziness quantifies vagueness with membership functions, while nondeterminism describes multiple possible outcomes without probability assignments.
Advantages and Limitations of Fuzzy Systems
Fuzzy systems excel at handling imprecise and uncertain information by mimicking human reasoning, making them highly effective for applications like control systems, decision-making, and pattern recognition where binary true/false logic falls short. Their advantages include flexibility, robustness to noisy data, and the ability to incorporate expert knowledge through linguistic variables and fuzzy rules. However, fuzzy systems face limitations in scalability for complex problems, challenges in rule base development, and difficulties ensuring global consistency and interpretability in large-scale implementations.
Nondeterministic Methods: Strengths and Drawbacks
Nondeterministic methods excel in exploring multiple computational paths simultaneously, enabling efficient problem-solving in complex search spaces and optimization tasks. They inherently handle uncertainty by considering various possible outcomes, which is advantageous in scenarios like automata theory and parallel processing. However, their primary drawback lies in computational resource intensity, as exploring numerous possibilities can lead to exponential time complexity and significant memory consumption.
Choosing the Right Approach: Fuzzy or Nondeterministic?
Choosing between fuzzy and nondeterministic approaches depends on the nature of uncertainty and the complexity of the problem domain. Fuzzy systems excel in handling imprecise, gradual information by modeling degrees of truth, making them ideal for control systems and decision-making with vague data. Nondeterministic models represent multiple possible outcomes without probabilistic weights, suited for predictive analysis where exploring all potential paths or states is crucial.
Fuzzy Infographic
 libterm.com
libterm.com