Monoidal categories provide a framework in category theory where objects can be combined using a tensor product, accompanied by an identity object and natural isomorphisms satisfying coherence conditions. This structure is essential for understanding concepts in algebra, quantum computing, and topology by enabling the manipulation of complex systems via simple compositional rules. Discover how monoidal categories can deepen Your insight into abstract mathematical structures by exploring the rest of this article.
Table of Comparison
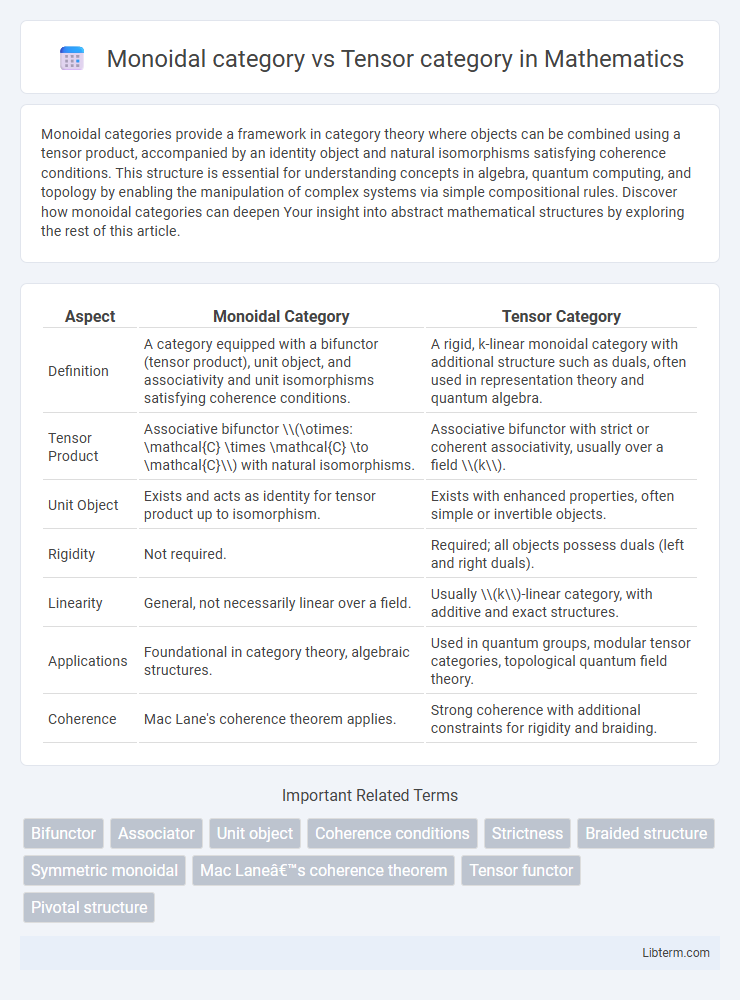
| Aspect | Monoidal Category | Tensor Category |
|---|---|---|
| Definition | A category equipped with a bifunctor (tensor product), unit object, and associativity and unit isomorphisms satisfying coherence conditions. | A rigid, k-linear monoidal category with additional structure such as duals, often used in representation theory and quantum algebra. |
| Tensor Product | Associative bifunctor \\(\otimes: \mathcal{C} \times \mathcal{C} \to \mathcal{C}\\) with natural isomorphisms. | Associative bifunctor with strict or coherent associativity, usually over a field \\(k\\). |
| Unit Object | Exists and acts as identity for tensor product up to isomorphism. | Exists with enhanced properties, often simple or invertible objects. |
| Rigidity | Not required. | Required; all objects possess duals (left and right duals). |
| Linearity | General, not necessarily linear over a field. | Usually \\(k\\)-linear category, with additive and exact structures. |
| Applications | Foundational in category theory, algebraic structures. | Used in quantum groups, modular tensor categories, topological quantum field theory. |
| Coherence | Mac Lane's coherence theorem applies. | Strong coherence with additional constraints for rigidity and braiding. |
Introduction to Monoidal Categories and Tensor Categories
Monoidal categories provide a framework in category theory where objects and morphisms are equipped with a tensor product, associativity constraints, and a unit object, enabling the study of compositional structures. Tensor categories are specialized monoidal categories characterized by additional properties such as rigidity, abelian structure, or semisimplicity, often appearing in representation theory and quantum algebra. Understanding the subtle distinctions between general monoidal categories and tensor categories is crucial for applications in areas like higher algebra and topological quantum field theory.
Historical Development and Context
Monoidal categories, introduced by Saunders Mac Lane in the 1960s, formalized the notion of tensor product structures in category theory, providing a framework to study associativity and unit objects up to natural isomorphisms. Tensor categories emerged later as a refinement, particularly in the context of representation theory and quantum algebra, emphasizing rigid, often braided, monoidal categories with duals and additional algebraic structure. The historical development reflects a shift from abstract categorical foundations toward specialized structures facilitating applications in topological quantum field theory and modular tensor categories.
Fundamental Definitions
A monoidal category is defined by a category equipped with a bifunctor called the tensor product, an identity object, and natural isomorphisms that satisfy coherence conditions such as associativity and unit constraints. A tensor category extends the concept of a monoidal category by incorporating additional structures like duals for objects, making it rigid, and often includes linearity over a field, typically used in representation theory and quantum algebra. Fundamental definitions emphasize the structural coherence in monoidal categories, while tensor categories focus on enriched structures and properties that enable advanced algebraic and categorical manipulations.
Key Structures: Monoidal vs Tensor Categories
Monoidal categories consist of a category equipped with a bifunctor called the tensor product, an identity object, and natural isomorphisms satisfying coherence conditions such as associativity and unit laws. Tensor categories are a special class of monoidal categories that are rigid, abelian, and often equipped with additional structure like duals and a compatible linear or braided structure, commonly arising in representation theory and quantum algebra. The key distinction lies in tensor categories having stronger algebraic properties and rigidity requirements, enhancing the structural framework beyond the foundational axioms of monoidal categories.
Associativity and Unit Constraints
Monoidal categories feature associativity and unit constraints expressed through natural isomorphisms that satisfy coherence conditions, ensuring the tensor product operation is associative up to isomorphism and has a unit object acting as an identity. Tensor categories extend monoidal categories with additional structures such as rigidity, braiding, or symmetry, but retain the associativity and unit constraints as foundational axioms. The associativity constraint is an isomorphism \( \alpha_{X,Y,Z} : (X \otimes Y) \otimes Z \cong X \otimes (Y \otimes Z) \), and the unit constraints \( \lambda_X : I \otimes X \cong X \) and \( \rho_X : X \otimes I \cong X \) ensure the tensor unit \( I \) behaves as an identity object within both category types.
Symmetry and Braiding: A Comparative View
Monoidal categories provide a framework with an associative tensor product and a unit object, allowing for binary operations within a categorical structure; however, they do not inherently assume symmetry or braiding. Tensor categories extend monoidal categories by incorporating additional properties such as symmetry, where the tensor product commutes up to a natural isomorphism, or braiding, which introduces a controlled, non-symmetric interchange of objects reflecting rich algebraic structures. The presence of braiding or symmetry in tensor categories enables applications in quantum groups, knot theory, and modular tensor categories, distinguishing them from general monoidal categories by their enhanced structural constraints and categorical coherence conditions.
Examples and Applications in Mathematics
Monoidal categories generalize tensor categories by relaxing strict associativity and unit constraints, allowing broader applications in higher category theory and homotopy theory. For example, the category of vector spaces with the usual tensor product forms a strict tensor category widely used in representation theory and quantum groups. Monoidal categories find applications in topological quantum field theory and knot invariants, while tensor categories are essential in modular tensor categories, operator algebras, and conformal field theory.
Relation to Representation Theory
Monoidal categories provide a categorical framework for tensor product operations that generalize associative algebras, playing a crucial role in studying the representations of algebraic structures such as groups, Lie algebras, and Hopf algebras. Tensor categories, often enriched with additional structures like rigidity or braiding, serve as settings for modular tensor categories and fusion categories, key in describing modular invariants and quantum group representations. Both categories enable the formulation and analysis of intertwining operators and tensor product decompositions, fundamental aspects in representation theory and quantum topology.
Main Differences and Similarities
A monoidal category is a category equipped with a tensor product, an associativity constraint, and a unit object satisfying coherence conditions, forming the foundational structure for tensor categories. A tensor category extends this by usually requiring additional properties such as being abelian, rigid, or linear over a field, making it suitable for representation theory and quantum algebra. Both structures share the core concept of a tensor product and unit object but differ primarily in the categorical and algebraic properties imposed on tensor categories for richer applications.
Conclusion and Future Directions
Monoidal categories provide a foundational algebraic framework characterized by associativity and unit constraints, while tensor categories extend this structure with additional properties such as rigidity and duals, enabling richer representation theories. The comparison highlights tensor categories as pivotal in areas like quantum algebra and topological field theory due to their enhanced structural capabilities. Future research may focus on classifying tensor categories, exploring their applications in higher category theory, and developing computational tools for handling their complex morphisms.
Monoidal category Infographic
 libterm.com
libterm.com