Constant values play a crucial role in programming by providing fixed data that does not change during program execution, enhancing code reliability and readability. Understanding how to declare and use constants efficiently can prevent errors caused by accidental modification and improve overall software performance. Explore the rest of the article to learn how constants can optimize your coding practices.
Table of Comparison
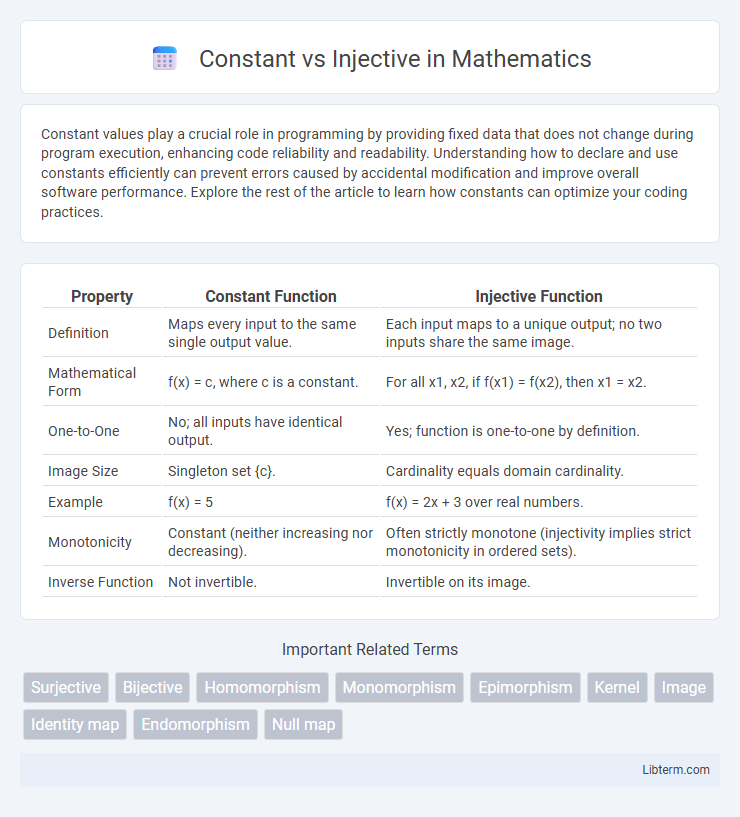
| Property | Constant Function | Injective Function |
|---|---|---|
| Definition | Maps every input to the same single output value. | Each input maps to a unique output; no two inputs share the same image. |
| Mathematical Form | f(x) = c, where c is a constant. | For all x1, x2, if f(x1) = f(x2), then x1 = x2. |
| One-to-One | No; all inputs have identical output. | Yes; function is one-to-one by definition. |
| Image Size | Singleton set {c}. | Cardinality equals domain cardinality. |
| Example | f(x) = 5 | f(x) = 2x + 3 over real numbers. |
| Monotonicity | Constant (neither increasing nor decreasing). | Often strictly monotone (injectivity implies strict monotonicity in ordered sets). |
| Inverse Function | Not invertible. | Invertible on its image. |
Understanding Constant Functions
Constant functions map every input in their domain to the same single output, making their range a single-value set. Unlike injective functions, which assign distinct outputs to distinct inputs, constant functions are not one-to-one and fail the horizontal line test. Understanding constant functions is essential for analyzing function behavior and distinguishing between types of mappings in mathematical analysis.
Defining Injective Functions
Injective functions, also known as one-to-one functions, map each element of the domain to a unique element in the codomain, ensuring no two distinct inputs share the same output. In contrast, constant functions assign the same output value to every input, lacking the injective property. Understanding these definitions highlights the importance of injective functions in establishing reversible mappings and preserving distinctness across elements.
Key Differences between Constant and Injective Functions
Constant functions map every element in the domain to a single fixed value in the codomain, resulting in zero variation and lacking injectivity. Injective functions, also known as one-to-one functions, assign distinct outputs to distinct inputs, ensuring no two different domain elements share the same image. The key difference lies in that constant functions are never injective unless the domain is a singleton, while injective functions maintain unique mappings across their entire domain.
Mathematical Representation of Constant vs Injective
A constant function is mathematically represented as f(x) = c, where c is a fixed constant and the output remains the same for every input x in the domain. An injective function, or one-to-one function, follows the rule that if f(x1) = f(x2), then x1 must equal x2, ensuring unique outputs for distinct inputs. The key difference lies in mapping: constant functions collapse the entire domain to a single value, whereas injective functions maintain distinctness across domain elements.
Graphical Interpretations
A constant function's graph is a horizontal line where every input maps to the same output, visually representing zero variation and no one-to-one correspondence. An injective function's graph passes the horizontal line test, ensuring that no horizontal line intersects the curve more than once, which means each input maps to a unique output. These graphical features distinctly illustrate that constant functions are not injective, while injective functions maintain a one-to-one mapping on their domain.
Real-Life Examples of Constant Functions
Constant functions maintain the same output value regardless of the input, such as a flat fee for shipping or a fixed interest rate in finance. In contrast, injective functions map each input to a unique output, like assigning a unique employee ID to each worker. Understanding these differences helps in modeling scenarios where outputs either remain unchanged or must uniquely correspond to inputs.
Real-Life Examples of Injective Functions
Injective functions, where each input maps to a unique output, are crucial in real-life scenarios like social security numbers assigning a distinct ID to each individual, ensuring no two people share the same number. In contrast, constant functions map every input to the same output, such as a fixed room temperature setting regardless of external conditions. Understanding injective functions helps in designing systems requiring one-to-one correspondences, such as database keys and encryption algorithms.
Importance in Mathematics and Computer Science
Constant functions assign the same output value for every input, serving as fundamental examples in mathematical analysis and system design due to their predictable behavior. Injective functions map distinct inputs to distinct outputs, which is crucial in computer science for data encoding, cryptography, and ensuring uniqueness in database keys. Understanding the differences between constant and injective functions helps optimize algorithms and supports the development of secure, efficient computational systems.
Common Misconceptions
Constant and injective functions are often confused due to their contrasting behavior; a constant function maps every input to the same output, resulting in zero injectivity, whereas an injective function assigns distinct outputs to distinct inputs. A common misconception is believing a constant function can be injective when defined over a single-element domain, but this is trivially true and not representative of general injectivity. Understanding the difference hinges on the mapping characteristics: injectivity requires uniqueness in outputs, while constancy enforces uniform output regardless of input variations.
Summary Table: Constant vs Injective
A constant function maps every input in its domain to the same single output value, resulting in a lack of distinct mapping between domain and codomain elements. An injective function, or one-to-one function, assigns unique outputs to each input, ensuring no two different inputs share the same output. The summary table compares these properties by highlighting that constant functions are not injective except in trivial cases, whereas injective functions guarantee distinct images for all domain elements.
Constant Infographic
 libterm.com
libterm.com