The Sierpinski set is a fascinating example of a fractal with intricate self-similar patterns emerging at every scale. This mathematical construct reveals complex geometric structures that challenge traditional notions of dimension and measure. Explore the rest of the article to uncover the remarkable properties and applications of the Sierpinski set.
Table of Comparison
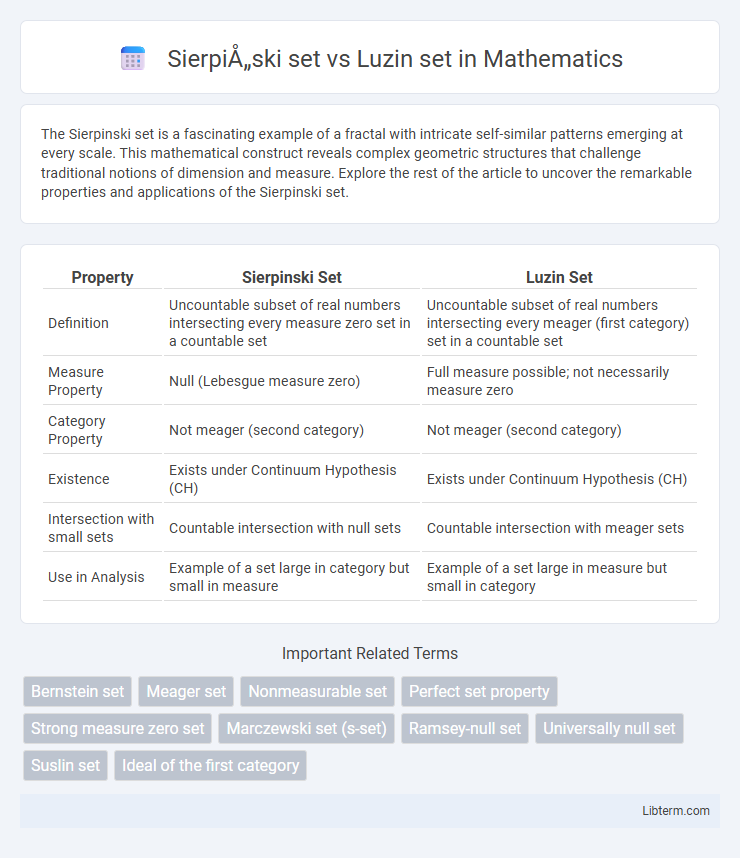
| Property | Sierpinski Set | Luzin Set |
|---|---|---|
| Definition | Uncountable subset of real numbers intersecting every measure zero set in a countable set | Uncountable subset of real numbers intersecting every meager (first category) set in a countable set |
| Measure Property | Null (Lebesgue measure zero) | Full measure possible; not necessarily measure zero |
| Category Property | Not meager (second category) | Not meager (second category) |
| Existence | Exists under Continuum Hypothesis (CH) | Exists under Continuum Hypothesis (CH) |
| Intersection with small sets | Countable intersection with null sets | Countable intersection with meager sets |
| Use in Analysis | Example of a set large in category but small in measure | Example of a set large in measure but small in category |
Introduction to Sierpiński and Luzin Sets
Sierpinski sets are uncountable subsets of the real numbers characterized by having countable intersection with every Lebesgue measure zero set, making them important in measure theory. Luzin sets, conversely, are uncountable subsets of the real numbers with the property that their intersection with every first category (meager) set is countable, central to the study of Baire category. Both sets highlight intricate structures in real analysis and descriptive set theory, illustrating the delicate interplay between measure and category.
Historical Background and Mathematical Context
The Sierpinski set, introduced by Waclaw Sierpinski in the early 20th century, is a subset of the real line with cardinality continuum that intersects every measure zero set in a countable set, reflecting early explorations in descriptive set theory and measure theory. The Luzin set, named after Nikolai Luzin, was constructed during the same period and consists of an uncountable subset of the real line where every countable subset is of the first category, emphasizing the interaction between category theory and real analysis. Both sets emerged from investigations into the foundations of real analysis and set theory, highlighting the intricate relationships between measure, category, and cardinal characteristics.
Definitions: Sierpiński Set
A Sierpinski set is an uncountable subset of the real numbers with the property that its intersection with any Lebesgue measure zero set is at most countable, highlighting its measure-theoretic thinness. Defined in the context of set theory and measure theory, a Sierpinski set contrasts with Luzin sets by focusing on measure rather than category. The existence of Sierpinski sets is independent of the standard ZFC axioms and requires additional hypotheses like the Continuum Hypothesis.
Definitions: Luzin Set
A Luzin set is an uncountable subset of the real numbers whose intersection with every meager set is countable, distinguishing it from typical large sets by its minimal overlap with sets of the first category. In contrast to a Sierpinski set, which has countable intersection with every null set, a Luzin set is specifically characterized by its behavior relative to meager sets in the real topology. These properties highlight the distinction between measure-theoretic smallness in Sierpinski sets and category-theoretic smallness in Luzin sets.
Key Properties and Characteristics
Sierpinski sets are uncountable subsets of the real numbers that intersect every measure-zero set in only countably many points, making them non-measurable and of strong combinatorial interest. Luzin sets are uncountable sets where every uncountable subset has positive outer measure but intersects every meager set in only countably many points, highlighting distinctive category-theoretic properties. Both sets exemplify unique interactions with measure and category, with Sierpinski sets emphasizing measure-theoretic null intersections and Luzin sets illustrating limits in category and measure overlap.
Differences Between Sierpiński and Luzin Sets
Sierpinski sets are subsets of the real line with cardinality continuum that intersect every measure zero set in only countably many points, highlighting their measure-theoretic sparsity. Luzin sets, conversely, are uncountable subsets whose intersection with every meager set is countable, emphasizing their category-theoretic thinness. The primary difference lies in Sierpinski sets avoiding large intersections with null sets (measure-zero), whereas Luzin sets avoid large intersections with meager (first category) sets.
Set-Theoretic Implications and Cardinalities
Sierpinski sets and Luzin sets occupy distinct positions in descriptive set theory with significant implications for cardinal characteristics of the continuum. A Sierpinski set is an uncountable subset of the real line intersecting every Lebesgue null set in only countably many points, while a Luzin set intersects every meager set countably; both sets have cardinality equal to the dominating number or the continuum under certain set-theoretic assumptions like the Continuum Hypothesis. Their existence highlights independence results in ZFC, affecting the structure of real line subsets, and impacts the interplay between measure and category, influencing cardinal invariants such as additivity of null and meager ideals.
Construction Methods and Existence
Sierpinski sets are constructed using transfinite induction under the Continuum Hypothesis (CH), producing subsets of the real line intersecting each measure zero set in at most countably many points. Luzin sets, also built assuming CH, are uncountable sets intersecting every meager set in only countably many points, constructed via careful selection through transfinite sequences to avoid meager sets. Both sets' existence is independent of ZFC, but their construction relies heavily on set-theoretic assumptions like CH to ensure the delicate combinatorial properties required.
Applications in Real Analysis and Set Theory
Sierpinski sets and Luzin sets play crucial roles in real analysis and set theory by exemplifying properties of measure and category. Sierpinski sets, subsets of the real line intersecting every null set in countably many points, are instrumental in studying Lebesgue measure and non-measurable sets. Luzin sets, uncountable sets intersecting every meager set in countably many points, are pivotal in exploring Baire category and functions with peculiar continuity properties.
Open Problems and Further Research Directions
The relationship between Sierpinski sets and Luzin sets remains central to open problems in descriptive set theory and set-theoretic topology, particularly regarding their existence under various set-theoretic axioms such as the Continuum Hypothesis and Martin's Axiom. Further research directions include exploring the consistency strength required for the existence of these sets and their generalized versions in larger cardinalities or different models of set theory. Investigations into the interplay between these sets and ideals, covering properties, and cardinal invariants of the continuum continue to reveal deeper structural insights and potential applications in real analysis and measure theory.
Sierpiński set Infographic
 libterm.com
libterm.com