A Gd set is a countable intersection of open sets in a topological space, often encountered in real analysis and descriptive set theory. These sets play a crucial role in understanding continuity, measurability, and Baire category properties. Explore the rest of the article to deepen your understanding of Gd sets and their applications.
Table of Comparison
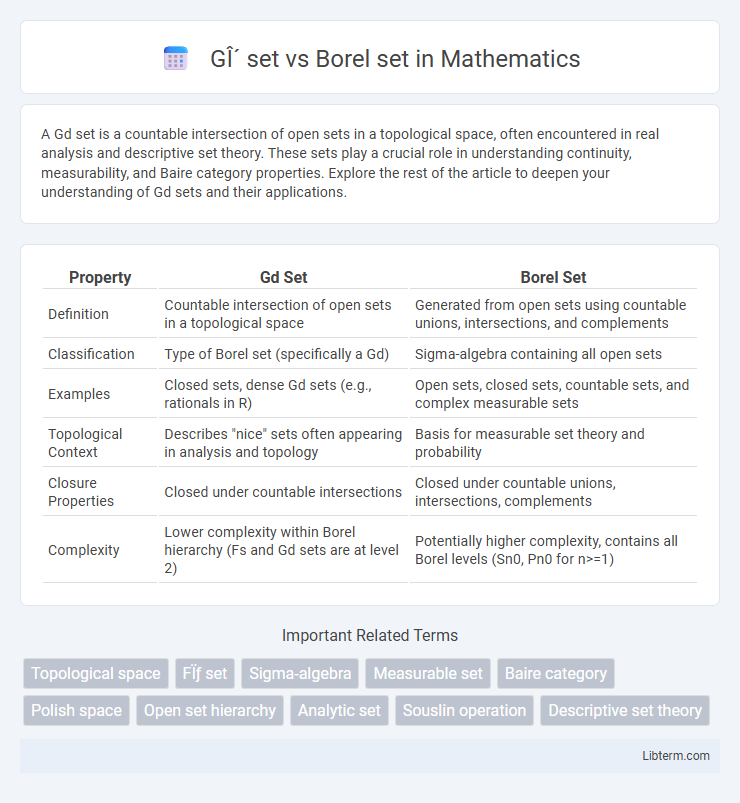
| Property | Gd Set | Borel Set |
|---|---|---|
| Definition | Countable intersection of open sets in a topological space | Generated from open sets using countable unions, intersections, and complements |
| Classification | Type of Borel set (specifically a Gd) | Sigma-algebra containing all open sets |
| Examples | Closed sets, dense Gd sets (e.g., rationals in R) | Open sets, closed sets, countable sets, and complex measurable sets |
| Topological Context | Describes "nice" sets often appearing in analysis and topology | Basis for measurable set theory and probability |
| Closure Properties | Closed under countable intersections | Closed under countable unions, intersections, complements |
| Complexity | Lower complexity within Borel hierarchy (Fs and Gd sets are at level 2) | Potentially higher complexity, contains all Borel levels (Sn0, Pn0 for n>=1) |
Introduction to Gδ Sets and Borel Sets
Gd sets are defined as countable intersections of open sets within a topological space, playing a crucial role in descriptive set theory and real analysis. Borel sets, generated from open sets through operations of countable union, countable intersection, and complement, form the smallest s-algebra containing all open sets, fundamental to measure theory and probability. Understanding the hierarchy and construction of Gd sets within Borel sets provides essential insights into measurable and topological properties of subsets in mathematical analysis.
Definitions: What Are Gδ Sets?
Gd sets are defined as countable intersections of open sets in a topological space, making them a key class of sets in descriptive set theory. Borel sets, more broadly, are generated through countable unions, countable intersections, and complements starting from open sets, encompassing all Gd sets within their hierarchy. Understanding Gd sets as specialized Borel sets provides insight into their topological and measure-theoretic properties.
Understanding Borel Sets
Borel sets form the smallest s-algebra containing all open sets in a topological space, crucial for measure theory and probability. Gd sets, defined as countable intersections of open sets, are specific examples of Borel sets, highlighting the intricate hierarchy within Borel s-algebras. Understanding Borel sets involves grasping their generation from open sets through countable unions, intersections, and complements, which enables the classification of complex measurable sets.
Hierarchies in Set Theory: Where Gδ and Borel Sets Fit
Gd sets are countable intersections of open sets and form a critical subclass within the Borel hierarchy, which organizes sets based on operations of countable unions and intersections starting from open sets. Borel sets encompass all sets that can be constructed from open sets through countable unions, intersections, and complements, stratifying into hierarchical levels such as S^0_1 (open sets), P^0_1 (closed sets), and extending to more complex classes like Gd (P^0_2) and Fs (S^0_2) sets. Understanding the placement of Gd sets within the Borel hierarchy is fundamental in descriptive set theory, as it highlights the increasing complexity and definability of sets under countable operations.
Key Properties of Gδ Sets
Gd sets are defined as countable intersections of open sets, making them a crucial subclass of Borel sets, which are generated by countable unions and intersections of open sets. A key property of Gd sets is their role in characterizing completely metrizable spaces, as every closed set in a complete metric space can be expressed as a Gd set. These sets also exhibit important measure-theoretic properties, such as being measurable and playing a significant role in descriptive set theory within Polish spaces.
Fundamental Properties of Borel Sets
Borel sets form the smallest s-algebra containing all open sets in a topological space, essential for defining measurable functions and measures. Gd sets, as countable intersections of open sets, are always Borel sets but represent a more specific subclass within the Borel hierarchy. Fundamental properties of Borel sets include closure under countable unions, countable intersections, and complements, enabling their application in measure theory and descriptive set theory.
Relationship Between Gδ Sets and Borel Sets
Gd sets are countable intersections of open sets, forming a subclass of Borel sets, which are generated by countable unions and intersections of open sets through transfinite operations. Every Gd set is inherently a Borel set, but not all Borel sets qualify as Gd due to the broader construction rules of Borel s-algebras. This relationship reflects the hierarchical structure within descriptive set theory, where Gd sets represent a specific topological complexity inside the extensive Borel classification.
Examples Illustrating Gδ Sets vs Borel Sets
The set of rational numbers \(\mathbb{Q}\) is a classic example of a Borel set that is not Gd, as it can be expressed as a countable union of singleton points but cannot be represented as a countable intersection of open sets. Conversely, the set of real numbers \(\mathbb{R}\) minus a single point is a Gd set since it can be represented as a countable intersection of open intervals. These examples illustrate that while all Gd sets are Borel sets of the first class, not all Borel sets are Gd sets, highlighting the distinction within the Borel hierarchy.
Applications in Topology and Measure Theory
Gd sets, defined as countable intersections of open sets, play a crucial role in topology by characterizing completely metrizable spaces and supporting the formulation of Baire category theorems. In measure theory, Borel sets, generated from open sets through countable unions, intersections, and complements, form the foundational s-algebra for defining standard measures like Lebesgue measure. The interplay between Gd and Borel sets enables refined classification of measurable functions and sets, facilitating advanced analysis in descriptive set theory and probability.
Summary: Distinguishing Gδ Sets from Borel Sets
Gd sets are defined as countable intersections of open sets, making them a specific subset within the broader Borel hierarchy. Borel sets encompass all sets that can be formed through countable unions, intersections, and complements of open sets, resulting in a more comprehensive classification. The key distinction lies in Gd sets being strictly constructed from open sets via intersections, whereas Borel sets include a wider array of operations, allowing for greater complexity in their structure.
Gδ set Infographic
 libterm.com
libterm.com