Regular expressions are powerful tools used to search, match, and manipulate text based on specific patterns, making them essential for programming and data analysis. You can use regular expressions to validate input, extract data, or perform complex text substitutions efficiently. Explore the rest of this article to master regular expressions and enhance your text processing skills.
Table of Comparison
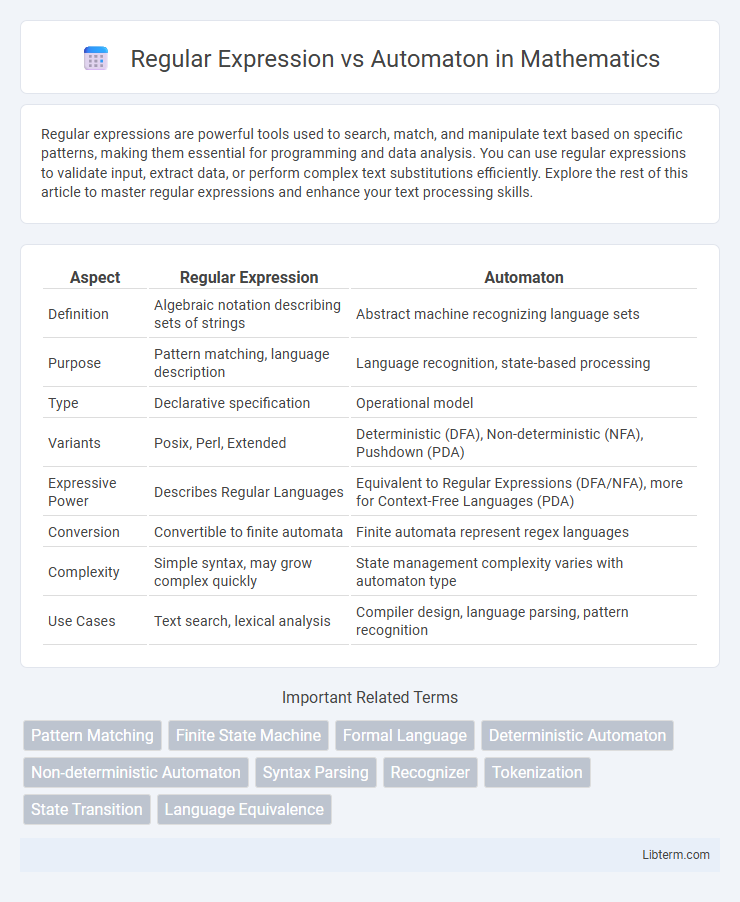
| Aspect | Regular Expression | Automaton |
|---|---|---|
| Definition | Algebraic notation describing sets of strings | Abstract machine recognizing language sets |
| Purpose | Pattern matching, language description | Language recognition, state-based processing |
| Type | Declarative specification | Operational model |
| Variants | Posix, Perl, Extended | Deterministic (DFA), Non-deterministic (NFA), Pushdown (PDA) |
| Expressive Power | Describes Regular Languages | Equivalent to Regular Expressions (DFA/NFA), more for Context-Free Languages (PDA) |
| Conversion | Convertible to finite automata | Finite automata represent regex languages |
| Complexity | Simple syntax, may grow complex quickly | State management complexity varies with automaton type |
| Use Cases | Text search, lexical analysis | Compiler design, language parsing, pattern recognition |
Introduction to Regular Expressions and Automata
Regular expressions define patterns for string matching using symbols and operators, forming the foundation for text search algorithms. Automata, such as finite automata, provide a computational model that recognizes these patterns, enabling efficient implementation of regular expressions. The theoretical equivalence between regular expressions and finite automata establishes a framework for analyzing language recognition and parsing in computer science.
Historical Background and Evolution
Regular expressions originated in the 1950s through the work of mathematician Stephen Kleene, who formalized them as a method to describe regular languages. Automata theory, developed concurrently by researchers such as Noam Chomsky and John Hopcroft, provided the abstract machine models that recognize these languages, including finite automata corresponding to regular expressions. Over time, both fields evolved hand-in-hand, with automata offering a computational framework that operationalizes the patterns defined by regular expressions, significantly impacting compiler design and formal language theory.
Core Concepts and Definitions
Regular expressions define patterns for string matching using symbols and operators such as concatenation, union, and Kleene star to represent sets of strings. Automata, including deterministic finite automata (DFA) and nondeterministic finite automata (NFA), provide computational models to recognize languages described by regular expressions through states and transitions. The equivalence between regular expressions and finite automata forms the foundation of formal language theory, enabling the conversion from pattern specifications to state machines for language recognition.
Mathematical Foundations
Regular expressions are formal language descriptors defining regular languages through pattern-based syntax, while automatons, such as finite automata, provide a state-based computational model recognizing these languages. The equivalence between regular expressions and finite automata is established by Kleene's theorem, demonstrating that every regular expression corresponds to a deterministic or nondeterministic finite automaton. This relationship forms the core mathematical foundation in automata theory, crucial for parsing algorithms and language recognition tasks.
Expressive Power: What Can They Represent?
Regular expressions and automata both represent regular languages, with automata such as deterministic finite automata (DFA) and nondeterministic finite automata (NFA) providing equivalent expressive power to that of regular expressions. Regular expressions concisely describe patterns using operators like union, concatenation, and Kleene star, while automata model these patterns through state transitions and acceptance conditions. Neither regular expressions nor finite automata can represent non-regular languages, highlighting their shared limitation in expressive power.
Syntax and Implementation Differences
Regular expressions use a symbolic syntax based on patterns such as literals, quantifiers, and character classes for string matching, while automata rely on states, transitions, and input symbols to process strings. Implementing regular expressions typically involves recursive parsing and backtracking algorithms, whereas automata are implemented through state machines, either deterministic (DFA) or nondeterministic (NFA), enabling efficient linear-time string recognition. The syntactic abstraction in regular expressions contrasts with the operational mechanics of automata, reflecting fundamental differences in their computational models and practical applications.
Applications in Computing
Regular expressions enable pattern matching in text processing tasks such as searching, validation, and data extraction, widely used in programming languages, compilers, and search engines. Automata, specifically finite automata, provide the theoretical foundation for implementing regular expressions effectively and are crucial in lexical analysis, protocol design, and model checking. The interplay between regular expressions and automata optimizes text parsing and formal language recognition in various computing applications.
Limitations and Challenges
Regular expressions face limitations in expressing certain language constructs that require memory beyond finite states, such as nested patterns or context-sensitive dependencies, which automata like pushdown automata can handle effectively. Automata can recognize a broader class of languages, including context-free languages, but they pose challenges in implementation complexity and increased computational resources compared to regular expressions. Both models have trade-offs where regular expressions excel in simplicity and efficiency for regular languages, while automata provide greater expressive power at the cost of higher complexity.
Performance and Efficiency Considerations
Regular expressions provide a compact syntax for pattern matching but can exhibit exponential time complexity in the worst case, especially with backtracking engines. Automata, particularly deterministic finite automata (DFA), offer linear time matching relative to input size, guaranteeing consistent performance with fixed memory overhead. Efficient implementation of automata allows for faster and more predictable matching, making them preferable in applications requiring high throughput and low latency.
Conclusion: Choosing Between Regular Expressions and Automata
Choosing between regular expressions and automata depends on the specific application requirements; regular expressions offer concise, human-readable pattern matching ideal for text processing, while automata provide formal, state-based models essential for computational verification and language recognition. Automata excel in scenarios demanding rigorous proofs of correctness, complexity analysis, and implementation in compilers, whereas regular expressions prioritize ease of use and rapid pattern identification. Understanding the theoretical equivalence but practical distinctions guides optimal selection for tasks involving lexical analysis, syntax parsing, or data validation.
Regular Expression Infographic
 libterm.com
libterm.com