A superlevel set consists of all points in a function's domain where the function values are greater than or equal to a specified threshold, playing a crucial role in mathematical analysis and optimization problems. Understanding superlevel sets helps in visualizing regions of interest, such as high-value areas in a dataset or function graph. Explore the rest of the article to see how superlevel sets impact various applications and why they are essential in your analytical toolkit.
Table of Comparison
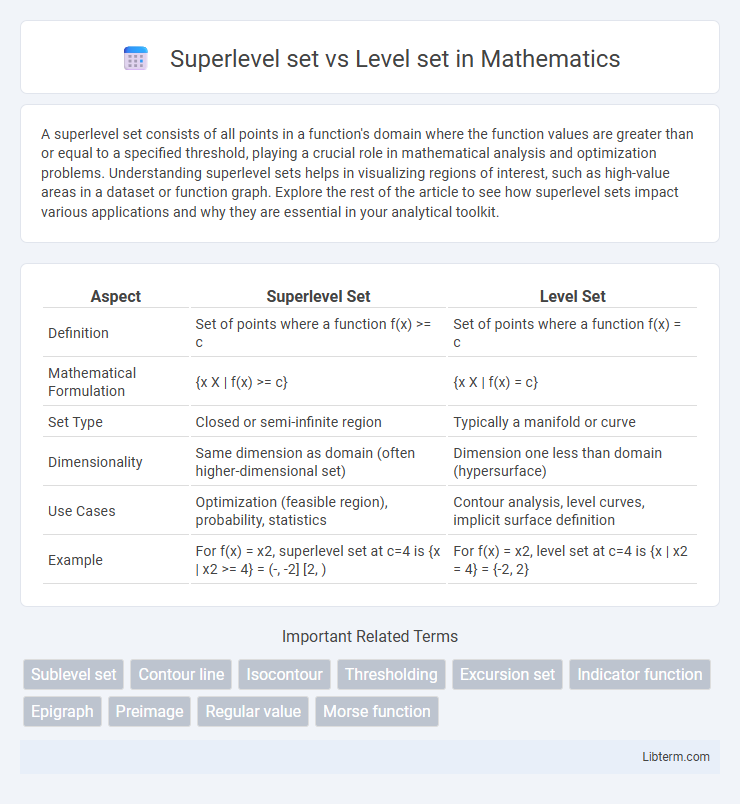
| Aspect | Superlevel Set | Level Set |
|---|---|---|
| Definition | Set of points where a function f(x) >= c | Set of points where a function f(x) = c |
| Mathematical Formulation | {x X | f(x) >= c} | {x X | f(x) = c} |
| Set Type | Closed or semi-infinite region | Typically a manifold or curve |
| Dimensionality | Same dimension as domain (often higher-dimensional set) | Dimension one less than domain (hypersurface) |
| Use Cases | Optimization (feasible region), probability, statistics | Contour analysis, level curves, implicit surface definition |
| Example | For f(x) = x2, superlevel set at c=4 is {x | x2 >= 4} = (-, -2] [2, ) | For f(x) = x2, level set at c=4 is {x | x2 = 4} = {-2, 2} |
Introduction to Level Sets and Superlevel Sets
Level sets represent the collection of points where a function equals a specific value, critical for analyzing shapes and interfaces in mathematics and computer vision. Superlevel sets encompass points where the function exceeds or equals a certain value, providing insight into regions of high intensity or significance. These concepts facilitate image segmentation, shape modeling, and topological analysis by capturing different thresholds of function values.
Mathematical Definitions
The superlevel set of a function f at a value a is defined as the set of points where f(x) is greater than or equal to a, formally {x | f(x) >= a}. In contrast, the level set is the collection of points where the function equals a specific value a, expressed as {x | f(x) = a}. Both concepts are fundamental in topology and analysis for describing contours and regions relevant to function behavior.
Key Differences Between Superlevel and Level Sets
Superlevel sets consist of points where a function's value is greater than or equal to a specified threshold, while level sets are defined by points where the function equals the threshold exactly. The superlevel set captures regions above the threshold, providing a broader area that includes the level set boundary, whereas the level set forms a precise contour or surface of constant function value. These key differences make superlevel sets useful in optimization and image processing for identifying regions of interest, while level sets are critical for geometric modeling and interface tracking.
Visual Representation and Interpretation
Superlevel sets and level sets provide distinct visual representations in mathematical analysis: a level set is the collection of points where a function equals a constant value, forming a contour line or surface, whereas a superlevel set includes all points where the function values are greater than or equal to that threshold, creating a filled region above the contour. Visually, level sets emphasize boundaries of constant value, useful for identifying exact feature contours, while superlevel sets highlight areas exceeding a certain intensity, aiding in threshold-based segmentation or decision-making. These interpretations are critical in fields like image processing, geographic information systems, and optimization, where understanding the spatial distribution of function values directly impacts analysis and outcomes.
Applications in Mathematics and Science
Superlevel sets identify regions where a function exceeds a given threshold, facilitating applications in optimization, machine learning, and image processing for feature extraction and decision boundaries. Level sets represent points where a function equals a specific value, crucial in numerical analysis, computer vision, and fluid dynamics for modeling interfaces and evolving shapes. Together, these sets enable advanced techniques in topology, geometry, and scientific computing, enhancing data visualization and shape analysis.
Superlevel Sets in Image Processing
Superlevel sets in image processing refer to regions where pixel intensities exceed a specified threshold, enabling efficient segmentation of high-intensity objects in noisy or complex images. Unlike level sets that represent contours at exact pixel values, superlevel sets capture all pixels above a threshold, supporting robust feature extraction and shape analysis. Applications leverage superlevel sets for tasks such as tumor detection, texture segmentation, and object recognition, benefiting from their stability under intensity variations.
Level Sets in Computational Methods
Level sets in computational methods represent contours where a function equals a constant, enabling precise tracking of evolving interfaces and shapes in multidimensional data. Unlike superlevel sets, which capture regions where the function exceeds a threshold, level sets provide exact boundary locations essential for applications in image processing, fluid dynamics, and shape optimization. Numerical techniques like the level set method use implicit surfaces to handle topological changes robustly, making them integral to advanced computational modeling and simulations.
Properties and Theorems
Superlevel sets, defined as regions where a function exceeds a given threshold, exhibit properties crucial in optimization and monotonicity analysis, often used to characterize convex functions through convex superlevel sets. Level sets, representing points where the function equals a constant, possess geometric and topological properties fundamental in differential geometry and PDE theory, including smoothness and regularity under differentiability conditions. Key theorems, such as Sard's theorem for level sets and quasi-concavity characterizations for superlevel sets, establish foundational links between function behavior and set structure in analysis.
Practical Examples and Use Cases
Superlevel sets and level sets are fundamental in analyzing functions, where superlevel sets consist of all points where the function value exceeds a certain threshold, and level sets include points where the function equals that threshold. In image processing, superlevel sets can segment regions of interest by grouping pixels brighter than a specified intensity, while level sets help extract precise contours of objects with exact brightness values. Geospatial analysis employs superlevel sets to identify areas with elevation above certain altitudes, whereas level sets delineate exact altitude contours for topographic mapping.
Conclusion and Summary
Superlevel sets and level sets serve distinct purposes in mathematical analysis and optimization; superlevel sets consist of all points where a function's value is greater than or equal to a threshold, aiding in identifying regions of interest above a certain level. Level sets capture points where the function takes on a specific value, providing detailed contour information and facilitating precise boundary characterization. In summary, superlevel sets highlight exceedance regions critical for feasibility and constraint analysis, while level sets map exact function values essential for topology and shape understanding.
Superlevel set Infographic
 libterm.com
libterm.com