Non-contractible spaces in topology are shapes that cannot be continuously shrunk to a single point without tearing or gluing, making them fundamental in understanding complex structures. These spaces showcase intriguing properties that distinguish them from contractible ones, impacting fields like robotics, data analysis, and quantum computing. Explore the rest of this article to uncover how non-contractible spaces influence your understanding of mathematical and practical problems.
Table of Comparison
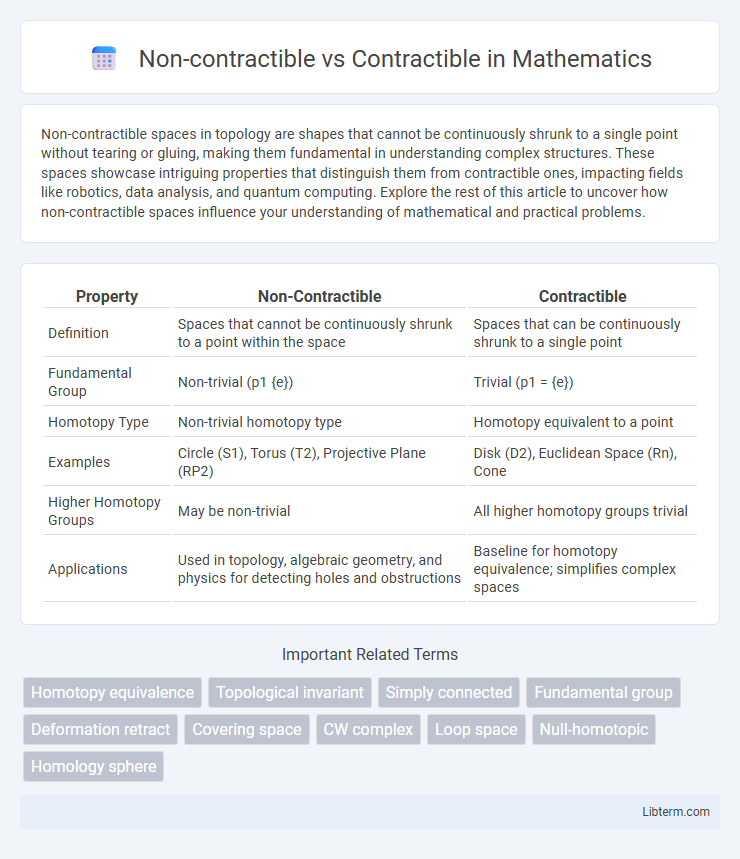
| Property | Non-Contractible | Contractible |
|---|---|---|
| Definition | Spaces that cannot be continuously shrunk to a point within the space | Spaces that can be continuously shrunk to a single point |
| Fundamental Group | Non-trivial (p1 {e}) | Trivial (p1 = {e}) |
| Homotopy Type | Non-trivial homotopy type | Homotopy equivalent to a point |
| Examples | Circle (S1), Torus (T2), Projective Plane (RP2) | Disk (D2), Euclidean Space (Rn), Cone |
| Higher Homotopy Groups | May be non-trivial | All higher homotopy groups trivial |
| Applications | Used in topology, algebraic geometry, and physics for detecting holes and obstructions | Baseline for homotopy equivalence; simplifies complex spaces |
Understanding Contractibility: Key Definitions
Contractibility refers to the property of a space being continuously shrunk to a point within that space, indicating it is homotopy equivalent to a single point. Non-contractible spaces cannot be reduced to a point without tearing or gluing, preserving essential topological features such as holes or loops. Understanding contractibility involves analyzing homotopy groups and deformation retracts to determine if a given space is contractible or non-contractible.
The Core Differences: Non-Contractible vs Contractible
Non-contractible spaces in topology exhibit properties where any loop cannot be continuously contracted to a single point, contrasting with contractible spaces that allow such deformation. This fundamental difference impacts homotopy groups, with non-contractible spaces having non-trivial higher homotopy groups while contractible spaces show trivial homotopy groups across all dimensions. Understanding these distinctions is essential in algebraic topology for classifying spaces and analyzing their intrinsic geometric and topological structures.
Real-World Examples of Contractible Entities
Contractible entities in topology, such as a solid sphere or a filled disk, can continuously shrink to a point within the space, exemplified by objects like soap bubbles or elastic membranes in the real world. Non-contractible entities, including a torus or a circle, possess holes or loops that prevent such continuous deformation, mirrored by structures like rubber bands or doughnuts. Understanding these distinctions aids in fields such as robotics, network topology, and molecular biology where shape and connectivity influence function.
Non-Contractible Structures in Practice
Non-contractible structures represent topological spaces that cannot be continuously shrunk to a point, exemplified by shapes like the torus or the Mobius strip. In practical applications, these structures are critical in fields such as robotics for motion planning, where non-contractibility ensures the presence of obstacles or holes affecting path connectivity. Understanding non-contractible loops aids in analyzing complex network topologies and designing resilient communication systems that rely on robust looping paths.
Mathematical Foundations of Contractibility
Contractibility in topology refers to a space that can be continuously shrunk to a point within that space, making it homotopy equivalent to a single point; such spaces are contractible. Non-contractible spaces lack this property, often characterized by nontrivial fundamental groups or higher homotopy groups, indicating the presence of holes or obstructions to deformation. Mathematical foundations of contractibility rely on homotopy theory, where contractible spaces have trivial homotopy groups, serving as key examples in algebraic topology for understanding deformation retracts and topological invariants.
Importance of Non-Contractible Spaces in Topology
Non-contractible spaces play a crucial role in topology by revealing essential properties of shape and structure that cannot be simplified to a point without tearing or gluing. These spaces, which cannot be continuously shrunk to a point, are fundamental in distinguishing topological spaces through invariants such as homotopy and homology groups. Understanding non-contractible spaces aids in classifying complex geometric forms and analyzing phenomena in algebraic topology, differential geometry, and applications like robotics and physics.
Applications of Contractible Concepts in Science
Contractible spaces play a crucial role in topology and algebraic geometry due to their property of being continuously shrinkable to a point, making them essential in fixed-point theorems and homotopy theory. Applications in physics include simplifying the study of configuration spaces in classical mechanics and quantum field theory, where contractible domains facilitate the analysis of field interactions. In computer science, contractible structures are used in data analysis and robotics for path planning and shape recognition, enhancing algorithmic efficiency and robustness.
Challenges in Identifying Non-Contractible Forms
Non-contractible forms present significant challenges in identification due to their complex topological structures that resist deformation into simpler, contractible shapes. These forms often arise in advanced mathematics and physics, where their inherent holes or twists prevent standard contractibility, complicating classification and analysis. Accurate detection requires sophisticated tools like algebraic topology invariants, such as homology or fundamental groups, to distinguish non-contractible entities from contractible counterparts.
Contractibility and Its Role in Problem Solving
Contractibility refers to the ability to continuously deform a space or shape into a single point without breaking or tearing, a key concept in topology and its applications in problem solving. Contractible spaces simplify complex structures by reducing them to trivial forms, enabling more efficient algorithms in areas like computer graphics, robotics, and data analysis. Understanding contractibility aids in detecting topological features, optimizing paths, and solving problems involving connectivity and shape deformation.
Future Research Directions: Exploring Contractibility
Future research on contractibility delves into topological spaces where any loop can continuously shrink to a point, contrasting with non-contractible spaces that contain essential loops resisting such deformation. Enhancing computational methods to distinguish contractible structures promises advancements in fields like robotics path planning and protein folding analysis. Investigating contractibility's role in higher-dimensional manifolds could reveal novel geometric properties and influence theoretical frameworks in algebraic topology and quantum computing algorithms.
Non-contractible Infographic
 libterm.com
libterm.com