A manifold is a mathematical space that locally resembles Euclidean space, allowing complex shapes to be analyzed with familiar geometric tools. These structures are fundamental in fields like topology, physics, and engineering, helping to describe curves, surfaces, and higher-dimensional spaces. Explore the rest of this article to understand how manifolds apply to your area of study or interest.
Table of Comparison
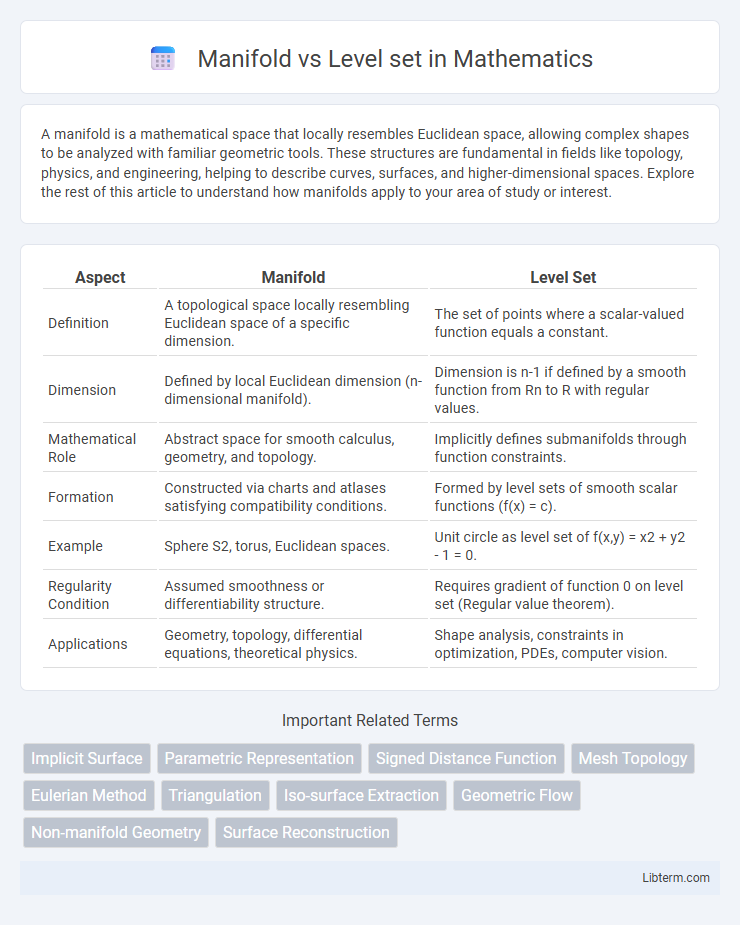
| Aspect | Manifold | Level Set |
|---|---|---|
| Definition | A topological space locally resembling Euclidean space of a specific dimension. | The set of points where a scalar-valued function equals a constant. |
| Dimension | Defined by local Euclidean dimension (n-dimensional manifold). | Dimension is n-1 if defined by a smooth function from Rn to R with regular values. |
| Mathematical Role | Abstract space for smooth calculus, geometry, and topology. | Implicitly defines submanifolds through function constraints. |
| Formation | Constructed via charts and atlases satisfying compatibility conditions. | Formed by level sets of smooth scalar functions (f(x) = c). |
| Example | Sphere S2, torus, Euclidean spaces. | Unit circle as level set of f(x,y) = x2 + y2 - 1 = 0. |
| Regularity Condition | Assumed smoothness or differentiability structure. | Requires gradient of function 0 on level set (Regular value theorem). |
| Applications | Geometry, topology, differential equations, theoretical physics. | Shape analysis, constraints in optimization, PDEs, computer vision. |
Introduction to Manifold and Level Set Methods
Manifold methods analyze geometric structures by representing data as continuous surfaces or higher-dimensional spaces embedded within a ambient space, enabling dimensionality reduction and feature extraction. Level set methods implicitly represent evolving contours or surfaces through a signed distance function, facilitating topological changes and curvature-driven flows in shape analysis or interface tracking. Both approaches provide powerful mathematical frameworks for modeling complex structures in fields like computer vision, graphics, and machine learning.
Core Concepts: Understanding Manifolds
Manifolds are topological spaces that locally resemble Euclidean space, providing a rigorous framework for studying geometric objects in higher dimensions. Each point on an n-dimensional manifold has a neighborhood homeomorphic to an open subset of R^n, enabling the application of calculus and differential geometry. This local Euclidean property distinguishes manifolds from more general sets, making them fundamental in fields like physics, robotics, and data analysis.
Core Concepts: Understanding Level Sets
Level sets represent contours of a higher-dimensional function where the function value remains constant, capturing interfaces and shapes implicitly. Manifolds generalize this concept as continuous, smooth surfaces that locally resemble Euclidean space of lower dimensions within higher-dimensional ambient spaces. Understanding level sets provides foundational insight into how manifolds can be described implicitly through scalar-valued functions, facilitating applications in geometry, physics, and data analysis.
Mathematical Foundations: Manifold vs Level Set
Manifolds are topological spaces that locally resemble Euclidean space and are defined by charts and atlases, providing a rigorous framework for smooth structures and differentiability. Level sets are defined as the set of points where a scalar function equals a constant, often used in implicit surface representations and characterized by the gradient conditions ensuring regularity. The mathematical foundation of manifolds encompasses a broader class of spaces with consistent dimension and smooth transitions, while level sets represent specific hypersurfaces derived from scalar functions within these manifolds.
Computational Approaches: Algorithms and Techniques
Manifold learning algorithms such as Isomap, Locally Linear Embedding (LLE), and t-SNE leverage neighborhood graphs and spectral methods to approximate low-dimensional structures in high-dimensional data, emphasizing global and local geometric properties respectively. Level set methods employ numerical PDE techniques, often using finite difference schemes to evolve contours implicitly through signed distance functions, enabling robust handling of topological changes in image segmentation and shape modeling. Computational approaches to manifolds focus on embedding and metric preservation, whereas level set algorithms prioritize curve evolution and interface tracking via Hamilton-Jacobi equations.
Advantages of Manifold Methods
Manifold methods excel in capturing intrinsic geometric structures of high-dimensional data by reducing dimensionality while preserving local continuity, enabling more efficient representation and analysis compared to level set approaches. These techniques offer robustness to noise and can model complex non-linear relationships without requiring explicit parametrization, which is often challenging in level set methods. Enhanced scalability and adaptability to various data types make manifold methods preferable for tasks such as pattern recognition, image processing, and data visualization.
Advantages of Level Set Methods
Level set methods provide significant advantages in handling complex shape deformations and topological changes, such as merging and splitting, without explicit parameterization. They offer a robust numerical framework for evolving interfaces on fixed grids, facilitating the capture of sharp corners and discontinuities. This implicit representation enhances stability and accuracy in simulations involving dynamic boundaries in computer vision and fluid dynamics.
Application Areas: Where Each Method Excels
Manifold learning excels in high-dimensional data visualization, dimensionality reduction, and feature extraction, particularly in fields such as computer vision, speech recognition, and bioinformatics where intrinsic low-dimensional structures must be uncovered. Level set methods are highly effective in image processing, computational geometry, and fluid dynamics for tracking evolving interfaces and shapes, benefiting applications like medical image segmentation, shape optimization, and dynamic surface modeling. The choice depends on whether the task involves understanding data geometry (manifold learning) or modeling dynamic boundaries and interfaces (level set).
Challenges and Limitations of Both Methods
Manifold methods face challenges in accurately capturing complex, high-dimensional data structures due to sensitivity to noise and computational intensity, often requiring large sample sizes to maintain fidelity. Level set approaches encounter limitations in handling topological changes and can struggle with numerical instability, especially in high dimensions or when evolving interfaces become highly irregular. Both techniques demand careful parameter tuning and suffer from scalability issues, which constrain their applicability in real-time or large-scale data analysis scenarios.
Choosing Between Manifold and Level Set Methods
Choosing between manifold and level set methods depends on the problem's geometric complexity and computational efficiency requirements. Manifold methods excel in low-dimensional, smooth surface representations ideal for parameterization and dimensionality reduction, while level set methods effectively handle topological changes and evolving interfaces in higher-dimensional spaces. Prioritizing computational stability and the need for capturing shape changes guides the selection between the explicit manifold approach and the implicit level set technique.
Manifold Infographic
 libterm.com
libterm.com