Lie algebra is a fundamental structure in abstract algebra used to study geometric and algebraic properties of continuous transformation groups and their symmetries. This algebraic system plays a crucial role in theoretical physics, differential geometry, and representation theory by providing tools to analyze infinitesimal transformations. Dive deeper into the article to explore how Lie algebras shape modern mathematics and physics.
Table of Comparison
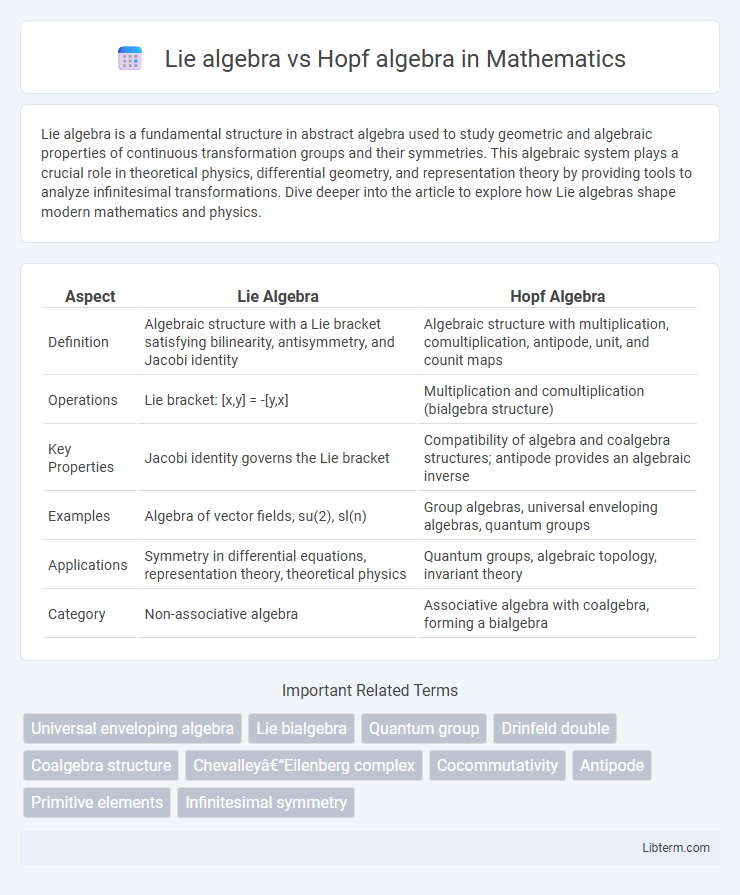
| Aspect | Lie Algebra | Hopf Algebra |
|---|---|---|
| Definition | Algebraic structure with a Lie bracket satisfying bilinearity, antisymmetry, and Jacobi identity | Algebraic structure with multiplication, comultiplication, antipode, unit, and counit maps |
| Operations | Lie bracket: [x,y] = -[y,x] | Multiplication and comultiplication (bialgebra structure) |
| Key Properties | Jacobi identity governs the Lie bracket | Compatibility of algebra and coalgebra structures; antipode provides an algebraic inverse |
| Examples | Algebra of vector fields, su(2), sl(n) | Group algebras, universal enveloping algebras, quantum groups |
| Applications | Symmetry in differential equations, representation theory, theoretical physics | Quantum groups, algebraic topology, invariant theory |
| Category | Non-associative algebra | Associative algebra with coalgebra, forming a bialgebra |
Introduction to Lie Algebras and Hopf Algebras
Lie algebras are algebraic structures primarily used to study the symmetry and linearization of Lie groups, characterized by a vector space equipped with a bilinear, antisymmetric Lie bracket satisfying the Jacobi identity. Hopf algebras extend this framework by combining algebra and coalgebra structures with a compatible antipode, facilitating the study of quantum groups, algebraic topology, and noncommutative geometry. Understanding Lie algebras involves grasping concepts like representations and universal enveloping algebras, whereas Hopf algebras emphasize coproducts, counits, and antipodes that encode algebraic symmetries in a categorical context.
Historical Background of Lie and Hopf Algebras
Lie algebras, introduced by Sophus Lie in the late 19th century, originated from the study of continuous transformation groups and provided a foundational framework for analyzing symmetries in differential equations. Hopf algebras emerged in the mid-20th century, developed by Heinz Hopf and others, as algebraic structures capturing essential properties of topological and algebraic objects in algebraic topology and quantum groups. The historical development of Lie and Hopf algebras reflects the evolution from classical symmetry theory to modern abstract algebraic structures with applications in geometry, physics, and representation theory.
Fundamental Definitions and Concepts
Lie algebras are algebraic structures defined by a vector space equipped with a bilinear, antisymmetric bracket satisfying the Jacobi identity, encapsulating the concept of infinitesimal symmetries in differential geometry and theoretical physics. Hopf algebras extend algebraic frameworks by combining associative algebra, coassociative coalgebra, antipode, counit, and unit maps, enabling the study of symmetry in both algebraic and coalgebraic contexts, particularly in quantum groups and noncommutative geometry. The fundamental distinction lies in Lie algebras focusing on bracket operations capturing infinitesimal automorphisms, while Hopf algebras encompass richer structures that facilitate dualities and module categories in algebraic topology and representation theory.
Algebraic Structures: Comparing Lie and Hopf Algebras
Lie algebras are algebraic structures characterized by a bilinear, antisymmetric bracket operation satisfying the Jacobi identity, primarily used to study continuous symmetries and differential equations. Hopf algebras extend the concept of algebra by incorporating a compatible coalgebra structure with an antipode map, enabling the study of groups, rings, and symmetry in a unified framework. The key distinction lies in Hopf algebras' ability to handle both algebraic and coalgebraic operations simultaneously, while Lie algebras focus on infinitesimal transformations within an algebraic setting.
Representation Theory for Lie and Hopf Algebras
Representation theory of Lie algebras explores linear actions of Lie algebras on vector spaces, providing fundamental tools for understanding symmetry and structure in algebra and geometry, characterized by weight spaces and root systems. Hopf algebra representation theory extends this framework by examining modules over Hopf algebras, which combine algebraic structures including associative algebras, coalgebras, and antipodes, facilitating a rich interplay between algebra and category theory, especially in quantum groups. While Lie algebra representations often focus on highest weight modules and simple modules classified by Lie type, Hopf algebra representations enable the study of more general symmetries, including noncommutative and quantum symmetries, broadening applications in mathematical physics and topology.
Applications in Mathematics and Physics
Lie algebras play a crucial role in the study of continuous symmetries and are fundamental in differential geometry, representation theory, and particle physics, particularly in the classification of elementary particles and gauge theories. Hopf algebras provide a key algebraic framework for quantum groups, noncommutative geometry, and the algebraic formulation of renormalization in quantum field theory. Both structures enable the exploration of symmetry-related concepts but differ in their algebraic properties and applications in integrable systems and topological quantum field theories.
Morphisms and Homomorphisms: Structural Differences
Lie algebras feature morphisms that preserve the Lie bracket, ensuring the antisymmetric and bilinear properties remain intact, while Hopf algebras have homomorphisms that maintain algebra, coalgebra, and antipode structures simultaneously. Homomorphisms in Hopf algebras are more complex, requiring compatibility with multiplication, comultiplication, unit, counit, and antipode maps, reflecting their richer algebraic and coalgebraic nature. Lie algebra morphisms primarily emphasize preserving the Lie bracket operation, which defines the algebraic structure through commutators.
Dualities and Connections Between Lie and Hopf Algebras
Lie algebras and Hopf algebras exhibit deep dualities, where the universal enveloping algebra of a Lie algebra forms a cocommutative Hopf algebra structure, linking Lie brackets to coproducts. The dual space of a cocommutative Hopf algebra often carries a Lie coalgebra structure, establishing a bidirectional correspondence crucial in quantum group theory. This interplay enables the translation of algebraic operations into coalgebraic frameworks, fostering advanced study of symmetries and deformations in mathematical physics.
Examples and Constructions of Lie vs. Hopf Algebras
Lie algebras are typically constructed from algebraic structures like vector spaces equipped with a Lie bracket, exemplified by \(\mathfrak{gl}_n(\mathbb{C})\), the algebra of all \(n \times n\) complex matrices with the commutator bracket. Hopf algebras, in contrast, arise from algebraic structures that combine algebra and coalgebra properties, with examples including group algebras and the universal enveloping algebra \(U(\mathfrak{g})\) of a Lie algebra \(\mathfrak{g}\), which itself carries a Hopf algebra structure. The construction of a Hopf algebra typically involves defining compatible operations such as multiplication, unit, comultiplication, counit, and antipode, illustrating a richer algebraic framework compared to the bracket-focused construction of Lie algebras.
Future Directions and Open Problems in Algebraic Theory
Exploration of Lie algebras and Hopf algebras continues to drive advancements in quantum groups and noncommutative geometry, with ongoing research targeting their categorification and representation theory. Open problems include the classification of infinite-dimensional Hopf algebras and understanding deformation quantization through Lie bialgebra structures. Future directions emphasize bridging the gap between algebraic and topological properties by developing new homological invariants and applying these frameworks to mathematical physics and quantum computing.
Lie algebra Infographic
 libterm.com
libterm.com