The bidual space, also known as the second dual, extends a given normed vector space by considering the dual of its dual space, often providing a richer structure that encapsulates all continuous linear functionals on the original space. This concept plays a crucial role in functional analysis, revealing insights about reflexivity and completeness that impact the behavior of operators and the geometry of Banach spaces. Explore the rest of the article to understand how your perspective on vector spaces deepens through the bidual space framework.
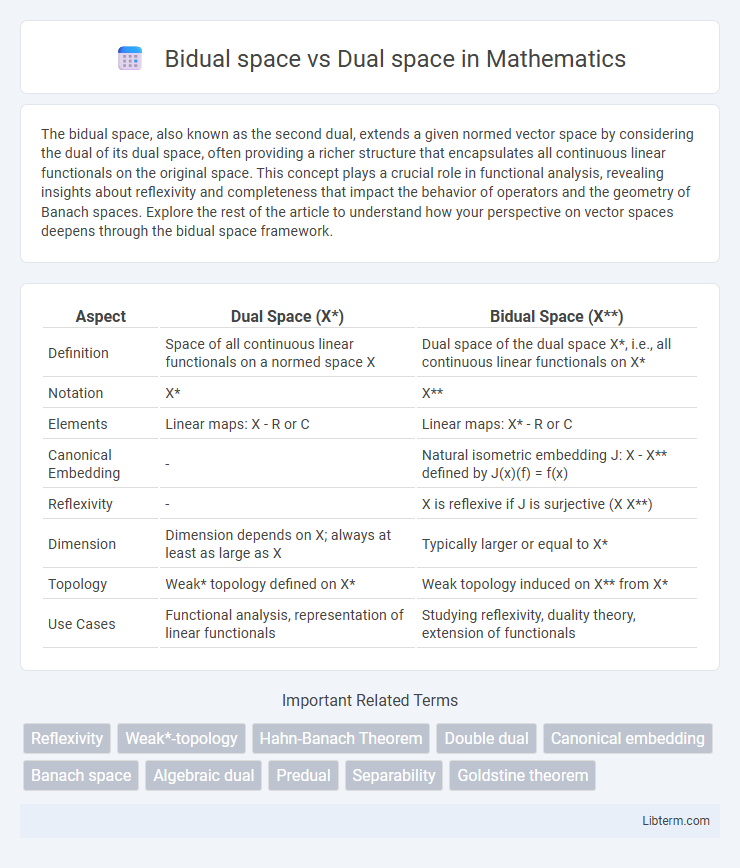
Table of Comparison
| Aspect | Dual Space (X*) | Bidual Space (X) |
|---|---|---|
| Definition | Space of all continuous linear functionals on a normed space X | Dual space of the dual space X*, i.e., all continuous linear functionals on X* |
| Notation | X* | X |
| Elements | Linear maps: X - R or C | Linear maps: X* - R or C |
| Canonical Embedding | - | Natural isometric embedding J: X - X defined by J(x)(f) = f(x) |
| Reflexivity | - | X is reflexive if J is surjective (X X) |
| Dimension | Dimension depends on X; always at least as large as X | Typically larger or equal to X* |
| Topology | Weak* topology defined on X* | Weak topology induced on X from X* |
| Use Cases | Functional analysis, representation of linear functionals | Studying reflexivity, duality theory, extension of functionals |
Introduction to Dual and Bidual Spaces
The dual space of a normed vector space consists of all continuous linear functionals mapping the space into its underlying field, typically the real or complex numbers. The bidual space is the dual of the dual space, containing continuous linear functionals acting on the dual space itself, usually leading to a natural embedding of the original space into its bidual. This embedding is isometric and linear, often a key concept in the study of reflexive spaces and functional analysis.
Fundamental Concepts: Vector Spaces and Linear Functionals
The dual space of a vector space V consists of all linear functionals mapping V to its underlying field, capturing the action of V via linear maps. The bidual space, or double dual, extends this concept by considering linear functionals on the dual space itself, often revealing properties of V through canonical embedding. Understanding these fundamental structures illuminates the interplay between vectors and linear functionals, crucial for advanced linear algebra and functional analysis.
Defining the Dual Space
The dual space of a normed vector space consists of all continuous linear functionals mapping from the space to its underlying field, typically the real or complex numbers. It captures the space of bounded linear transformations and plays a key role in functional analysis by facilitating the study of linear properties through duality. The bidual space is the dual of the dual space, often revealing reflexivity properties of the original space when canonical embeddings are considered.
What is the Bidual Space?
The bidual space, also known as the second dual, is the dual space of the dual space of a given normed vector space, often denoted as X for a space X. It consists of all continuous linear functionals defined on the dual space X*, capturing a broader range of functionals that may include evaluations beyond those in X itself. The natural embedding of X into its bidual X is always isometric, but surjectivity depends on whether X is reflexive, a property crucial in functional analysis and operator theory.
The Natural Embedding: Space into Double Dual
The natural embedding maps a normed vector space \( X \) isometrically into its bidual \( X^{} \), associating each element \( x \in X \) with the evaluation functional \( \hat{x} \) in \( X^{} \). This embedding preserves the norm and ensures \( X \) can be identified with a subspace of \( X^{} \), highlighting reflexivity when the map is surjective. The distinction between dual and bidual arises since the dual space \( X^* \) consists of bounded linear functionals on \( X \), while the bidual \( X^{} \) consists of bounded linear functionals on \( X^* \).
Reflexivity: When Bidual Equals the Original Space
The bidual space of a normed vector space is the dual of its dual space, often denoted as \(X^{}\), and reflexivity occurs when there is a natural isometric isomorphism between \(X\) and \(X^{}\). Reflexive Banach spaces satisfy the property \(X \cong X^{}\), meaning every element of the bidual corresponds uniquely to an element in the original space, ensuring the embedding of \(X\) into \(X^{}\) is surjective. Classic examples of reflexive spaces include \(L^p\) spaces for \(1 < p < \infty\), where the dual of the dual recovers the original space exactly, in contrast to non-reflexive spaces like \(L^1\) or \(C[0,1]\).
Differences between Dual and Bidual Spaces
The dual space consists of all continuous linear functionals defined on a normed vector space, while the bidual space is the dual of the dual space, containing continuous linear functionals acting on the dual space itself. A key difference lies in reflexivity: a normed space is reflexive if it is isometrically isomorphic to its bidual space, meaning elements of the original space can be identified with their image in the bidual. Dual spaces capture linear functionals on the original space, but bidual spaces often exhibit a richer structure, potentially extending beyond the image of the original space unless reflexivity holds.
Examples in Finite and Infinite Dimensions
The dual space of a vector space \( V \), denoted \( V^* \), consists of all linear functionals mapping \( V \) to its field of scalars, with finite-dimensional examples like \( \mathbb{R}^n \) having dual spaces isomorphic to \( \mathbb{R}^n \). In contrast, the bidual space \( V^{} \) contains functionals on \( V^* \), and in finite dimensions, the natural isomorphism \( V \cong V^{} \) holds, exemplified by \( \mathbb{R}^n \cong (\mathbb{R}^n)^*{}^* \). Infinite-dimensional Hilbert spaces, such as \( \ell^2 \), maintain this isomorphism via the Riesz representation theorem, while more general Banach spaces show strict inclusions \( V \subsetneq V^{} \), demonstrating distinct structural properties in their biduals compared to dual spaces.
Applications in Functional Analysis
The dual space of a normed vector space X consists of all continuous linear functionals on X, playing a critical role in defining weak topologies and studying bounded linear operators. The bidual space, or second dual, extends this by providing an isometric embedding of X into X, facilitating the analysis of reflexive spaces and characterizing the compactness properties of operators. Applications in functional analysis include the Hahn-Banach theorem, weak* convergence methods, and the representation of dual pairs, essential for optimization, PDEs, and spectral theory.
Conclusion: Key Insights on Dual and Bidual Spaces
Dual spaces consist of all continuous linear functionals defined on a given normed vector space, capturing essential properties of the original space through linear mappings. Bidual spaces extend this concept by considering the dual of the dual space, often embedding the original space isometrically into the bidual and revealing deeper structural features like reflexivity. Understanding the relationship between dual and bidual spaces enables critical insights into functional analysis, including the characterization of spaces where the canonical embedding is surjective, highlighting the importance of reflexive Banach spaces.
Bidual space Infographic
 libterm.com
libterm.com