Hermite polynomials are a class of orthogonal polynomials that arise in probability, physics, and numerical analysis, particularly in solving the quantum harmonic oscillator and in Gaussian quadrature. These polynomials exhibit unique recurrence relations and differential equations that make them essential tools in approximation theory and statistical mechanics. Explore this article to deepen your understanding of Hermite polynomials and their applications in your field.
Table of Comparison
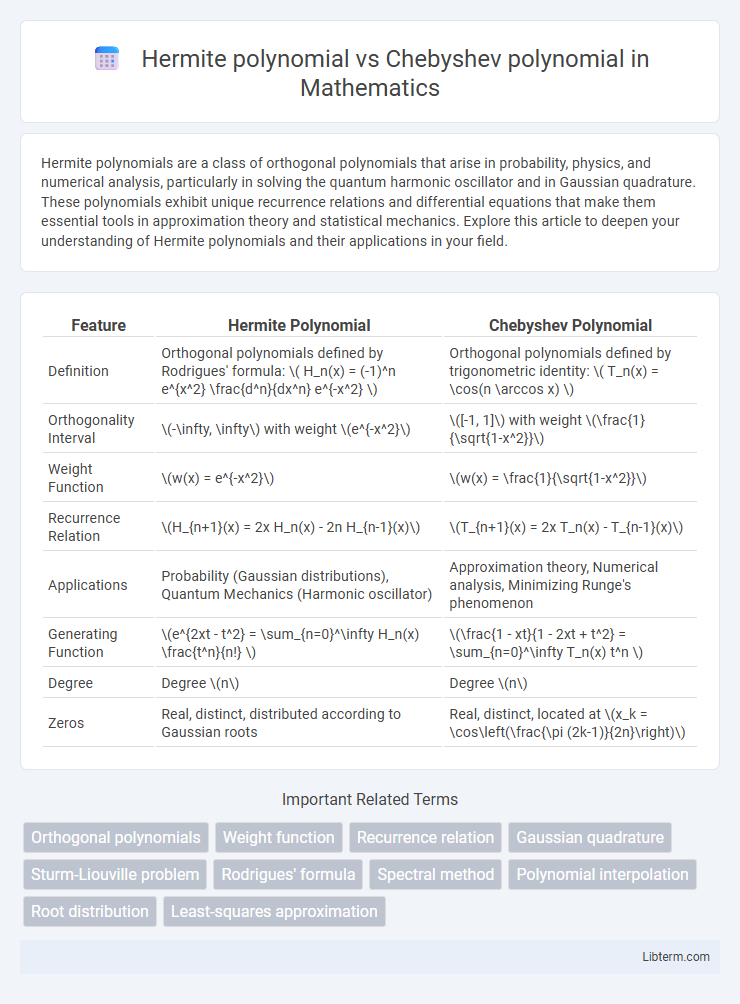
| Feature | Hermite Polynomial | Chebyshev Polynomial |
|---|---|---|
| Definition | Orthogonal polynomials defined by Rodrigues' formula: \( H_n(x) = (-1)^n e^{x^2} \frac{d^n}{dx^n} e^{-x^2} \) | Orthogonal polynomials defined by trigonometric identity: \( T_n(x) = \cos(n \arccos x) \) |
| Orthogonality Interval | \(-\infty, \infty\) with weight \(e^{-x^2}\) | \([-1, 1]\) with weight \(\frac{1}{\sqrt{1-x^2}}\) |
| Weight Function | \(w(x) = e^{-x^2}\) | \(w(x) = \frac{1}{\sqrt{1-x^2}}\) |
| Recurrence Relation | \(H_{n+1}(x) = 2x H_n(x) - 2n H_{n-1}(x)\) | \(T_{n+1}(x) = 2x T_n(x) - T_{n-1}(x)\) |
| Applications | Probability (Gaussian distributions), Quantum Mechanics (Harmonic oscillator) | Approximation theory, Numerical analysis, Minimizing Runge's phenomenon |
| Generating Function | \(e^{2xt - t^2} = \sum_{n=0}^\infty H_n(x) \frac{t^n}{n!} \) | \(\frac{1 - xt}{1 - 2xt + t^2} = \sum_{n=0}^\infty T_n(x) t^n \) |
| Degree | Degree \(n\) | Degree \(n\) |
| Zeros | Real, distinct, distributed according to Gaussian roots | Real, distinct, located at \(x_k = \cos\left(\frac{\pi (2k-1)}{2n}\right)\) |
Introduction to Orthogonal Polynomials
Hermite polynomials and Chebyshev polynomials are fundamental examples of orthogonal polynomials with distinct weight functions and domains. Hermite polynomials are orthogonal with respect to the Gaussian weight \( e^{-x^2} \) on the entire real line, making them crucial in probability theory and quantum mechanics. Chebyshev polynomials, defined on the interval \([-1, 1]\) with the weight \( (1-x^2)^{-1/2} \), are widely used in numerical analysis and approximation theory due to their minimax properties and fast convergence.
Overview of Hermite Polynomials
Hermite polynomials are a classical family of orthogonal polynomials defined by the Rodrigues formula involving the Gaussian weight function \( e^{-x^2} \) on the real line, playing a crucial role in probability theory and quantum mechanics, especially in solving the quantum harmonic oscillator. They exhibit properties such as orthogonality, recurrence relations, and generating functions, making them valuable in numerical analysis and approximation theory. In comparison, Chebyshev polynomials, orthogonal with respect to a different weight on the interval \([-1,1]\), are primarily used for minimizing approximation errors in polynomial interpolation and spectral methods.
Overview of Chebyshev Polynomials
Chebyshev polynomials, defined by the recurrence relation T0(x)=1, T1(x)=x, and Tn+1(x)=2xTn(x)-Tn-1(x), are widely used in approximation theory due to their minimax property which minimizes the maximum error in polynomial interpolation. Unlike Hermite polynomials, which arise in probability and physics for solving the quantum harmonic oscillator, Chebyshev polynomials are orthogonal with respect to the weight function (1-x2)^(-1/2) on the interval [-1,1]. Their roots serve as optimal nodes for polynomial interpolation, significantly reducing Runge's phenomenon and enhancing numerical stability.
Mathematical Definitions and Formulations
Hermite polynomials \( H_n(x) \) are defined by the Rodrigues' formula \( H_n(x) = (-1)^n e^{x^2} \frac{d^n}{dx^n} e^{-x^2} \), satisfying the differential equation \( y'' - 2x y' + 2n y = 0 \). Chebyshev polynomials of the first kind \( T_n(x) \) are defined by the trigonometric identity \( T_n(\cos \theta) = \cos(n \theta) \) and satisfy the differential equation \( (1 - x^2) y'' - x y' + n^2 y = 0 \). Both polynomial families serve as orthogonal bases with respect to different weight functions: Hermite polynomials are orthogonal with weight \( e^{-x^2} \) on the real line, while Chebyshev polynomials are orthogonal with weight \( \frac{1}{\sqrt{1-x^2}} \) on the interval \([-1,1]\).
Orthogonality Properties and Weight Functions
Hermite polynomials exhibit orthogonality over the interval (-, ) with respect to the weight function \( e^{-x^2} \), making them essential in probabilistic and quantum mechanics applications. Chebyshev polynomials are orthogonal on the finite interval [-1, 1] concerning the weight function \( \frac{1}{\sqrt{1-x^2}} \), which is critical in approximation theory and numerical methods. Their distinct orthogonality properties and weight functions define their specialized roles in solving differential equations and polynomial approximations.
Recurrence Relations: Hermite vs Chebyshev
Hermite polynomials satisfy the recurrence relation \(H_{n+1}(x) = 2xH_n(x) - 2nH_{n-1}(x)\), emphasizing their role in probabilists' and physicists' formulations. Chebyshev polynomials of the first kind follow \(T_{n+1}(x) = 2xT_n(x) - T_{n-1}(x)\), reflecting their utility in approximation theory and numerical methods. The key difference lies in the coefficients: Hermite's recurrence involves a term proportional to \(n\), which affects orthogonality with respect to the Gaussian weight, while Chebyshev's is a simpler homogeneous linear recurrence linked to minimizing polynomial deviation on \([-1,1]\).
Applications in Numerical Analysis
Hermite polynomials excel in numerical solutions of differential equations, particularly in quantum mechanics and probabilistic models where Gaussian weights are prominent. Chebyshev polynomials provide optimal polynomial approximation with minimal maximum error, making them indispensable in spectral methods and interpolation tasks in numerical analysis. Both polynomials enable efficient function approximation but differ by Hermite's emphasis on unbounded domains and Gaussian weight, while Chebyshev focuses on minimizing error on bounded intervals.
Polynomial Approximation and Interpolation
Hermite polynomials excel in polynomial approximation by incorporating both function values and derivative information, yielding higher-order continuity and more accurate interpolation for smooth functions. Chebyshev polynomials optimize interpolation by minimizing Runge's phenomenon through their roots distribution, ensuring near-minimax approximation errors in function reconstruction across intervals. Both polynomial families serve crucial roles in numerical analysis, with Hermite polynomials favored in Hermite interpolation problems and Chebyshev polynomials widely used in spectral methods and minimax polynomial approximation.
Advantages and Limitations of Each Polynomial
Hermite polynomials offer strong advantages in probability and physics due to their orthogonality with respect to the Gaussian weight, making them ideal for solving differential equations in quantum mechanics and stochastic processes. Chebyshev polynomials excel in numerical analysis and approximation theory with their minimax property, minimizing the maximum error in polynomial interpolation, which enhances stability and convergence. However, Hermite polynomials can be less effective in uniform approximation tasks, while Chebyshev polynomials may struggle with weight functions outside their defined orthogonality interval, limiting their application in non-uniform weight scenarios.
Conclusion: Choosing Between Hermite and Chebyshev
Hermite polynomials excel in applications involving Gaussian weight functions and quantum mechanics due to their orthogonality on the entire real line, making them ideal for solving differential equations with normal distribution contexts. Chebyshev polynomials, defined on a finite interval with weight function inversely proportional to the square root of (1-x2), offer superior numerical stability and efficiency for approximation and interpolation, particularly in minimizing polynomial approximation errors. Selection depends on problem domain: Hermite is preferred for infinite domains and probabilistic models, while Chebyshev suits finite interval approximations and computational tasks requiring minimized maximal error.
Hermite polynomial Infographic
 libterm.com
libterm.com