Imaginary concepts allow you to explore ideas beyond the limits of reality, tapping into creativity and abstract thinking. These thoughts often spark innovation, art, and problem-solving by envisioning scenarios that don't yet exist. Discover how embracing imaginary worlds can enhance your thinking and inspire new possibilities in the rest of this article.
Table of Comparison
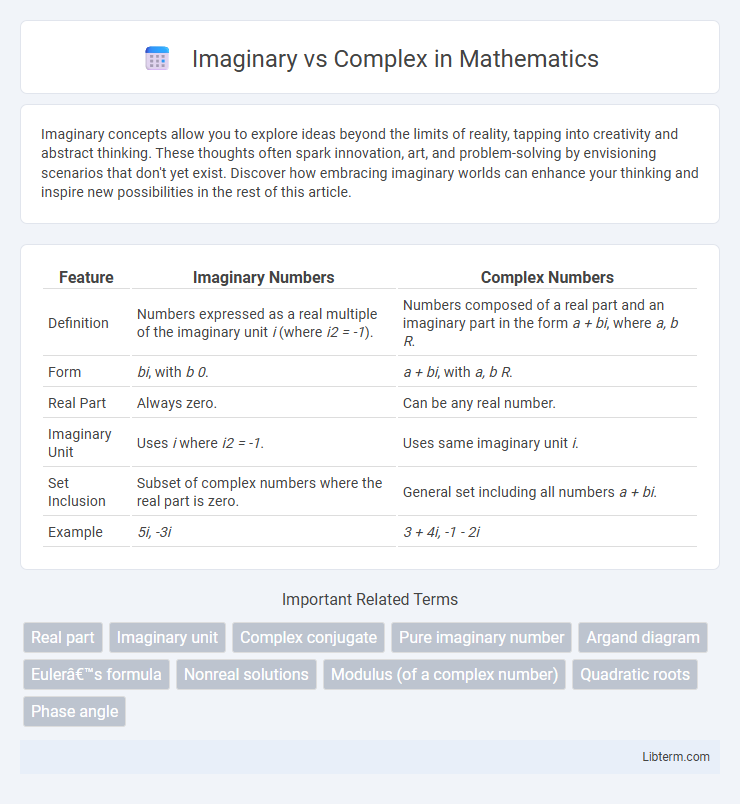
| Feature | Imaginary Numbers | Complex Numbers |
|---|---|---|
| Definition | Numbers expressed as a real multiple of the imaginary unit i (where i2 = -1). | Numbers composed of a real part and an imaginary part in the form a + bi, where a, b R. |
| Form | bi, with b 0. | a + bi, with a, b R. |
| Real Part | Always zero. | Can be any real number. |
| Imaginary Unit | Uses i where i2 = -1. | Uses same imaginary unit i. |
| Set Inclusion | Subset of complex numbers where the real part is zero. | General set including all numbers a + bi. |
| Example | 5i, -3i | 3 + 4i, -1 - 2i |
Introduction to Imaginary and Complex Numbers
Imaginary numbers are defined as multiples of the square root of -1, denoted as "i," where i2 = -1, providing a foundation beyond real numbers. Complex numbers combine real and imaginary parts in the form a + bi, where "a" represents the real component and "b" the imaginary coefficient, allowing representation of points on the complex plane. This system extends traditional arithmetic and enables solutions to equations that have no real solutions, such as quadratic equations with negative discriminants.
Defining Imaginary Numbers
Imaginary numbers are defined as multiples of the imaginary unit \(i\), where \(i\) satisfies the equation \(i^2 = -1\). Unlike complex numbers, which have both real and imaginary parts, imaginary numbers have a zero real part and a nonzero imaginary part. This distinct classification enables imaginary numbers to extend the real number system and facilitate solutions to equations that lack real roots.
Understanding Complex Numbers
Imaginary numbers are a subset of complex numbers characterized by a zero real part and a nonzero imaginary part, represented as bi where b is a real number and i is the imaginary unit defined by i2 = -1. Complex numbers consist of both a real part and an imaginary part in the form a + bi, where a and b are real numbers, enabling representation of a wider range of values on the complex plane. Understanding complex numbers involves exploring their algebraic properties, geometric interpretation, and applications in fields such as engineering, physics, and signal processing.
Key Differences Between Imaginary and Complex Numbers
Imaginary numbers are a subset of complex numbers where the real part is zero, expressed as bi with b as a nonzero real number and i representing the square root of -1. Complex numbers consist of both a real part and an imaginary part, written in the form a + bi, where a and b are real numbers. The key difference lies in their components: imaginary numbers have no real component, whereas complex numbers combine both real and imaginary components.
Mathematical Representation and Notation
Imaginary numbers are defined as multiples of the imaginary unit \( i \), where \( i^2 = -1 \), and are typically represented as \( bi \) with \( b \in \mathbb{R} \). Complex numbers combine both real and imaginary parts, written as \( a + bi \), where \( a \) and \( b \) are real numbers, encapsulating a two-dimensional number system in the complex plane. The mathematical notation distinguishes imaginary numbers as a subset of complex numbers with zero real part, while complex numbers include a real component enabling broader applications in fields like engineering and physics.
Geometric Interpretation in the Complex Plane
Imaginary numbers represent points on the vertical axis of the complex plane, corresponding to multiples of the imaginary unit \(i\), while complex numbers combine real and imaginary parts to indicate precise locations in a two-dimensional plane. Geometrically, complex numbers can be visualized as vectors originating from the origin, with their length denoting magnitude and angle representing the argument or phase. This interpretation facilitates operations like addition, multiplication, and finding magnitudes using geometric methods such as vector addition and polar coordinates.
Operations Involving Imaginary and Complex Numbers
Operations involving imaginary and complex numbers include addition, subtraction, multiplication, and division, where imaginary units (i, with i2 = -1) combine with real components to form complex numbers. Multiplying complex numbers requires applying the distributive property and using i2 = -1 for simplification, while division involves multiplying numerator and denominator by the complex conjugate to eliminate imaginary terms from the denominator. Complex arithmetic follows algebraic rules extended to incorporate imaginary units, enabling solutions to equations that lack real roots.
Real-World Applications
Imaginary numbers play a crucial role in signal processing, enabling the representation and manipulation of waveforms in electrical engineering. Complex numbers combine real and imaginary parts, forming the foundation for control systems, quantum mechanics, and fluid dynamics modeling. These mathematical tools facilitate the analysis of oscillations, electromagnetic waves, and system stability in various technological and scientific domains.
Common Misconceptions Clarified
Imaginary numbers, represented as multiples of the imaginary unit i, are often misunderstood as being separate from complex numbers, but in reality, they are a subset of complex numbers with zero real part. Complex numbers consist of both a real part and an imaginary part, expressed in the form a + bi, where a and b are real numbers and i2 = -1. Confusing imaginary numbers with purely imaginary or complex numbers obscures their fundamental relationship and usage in fields like engineering and physics.
Summary: Imaginary vs Complex Numbers
Imaginary numbers are a subset of complex numbers consisting of real multiples of the imaginary unit i, where i2 = -1. Complex numbers combine a real part and an imaginary part in the form a + bi, enabling solutions to equations without real roots. The distinction lies in that imaginary numbers represent purely non-real values, while complex numbers encompass both real and imaginary components.
Imaginary Infographic
 libterm.com
libterm.com