Aperiodic signals lack a fixed repeating pattern, making them fundamentally different from periodic signals that repeat at regular intervals. Their unpredictable nature is essential in various applications such as communications, where they represent transient phenomena or bursts of information. Discover how understanding aperiodic signals can enhance Your grasp of signal processing in the following article.
Table of Comparison
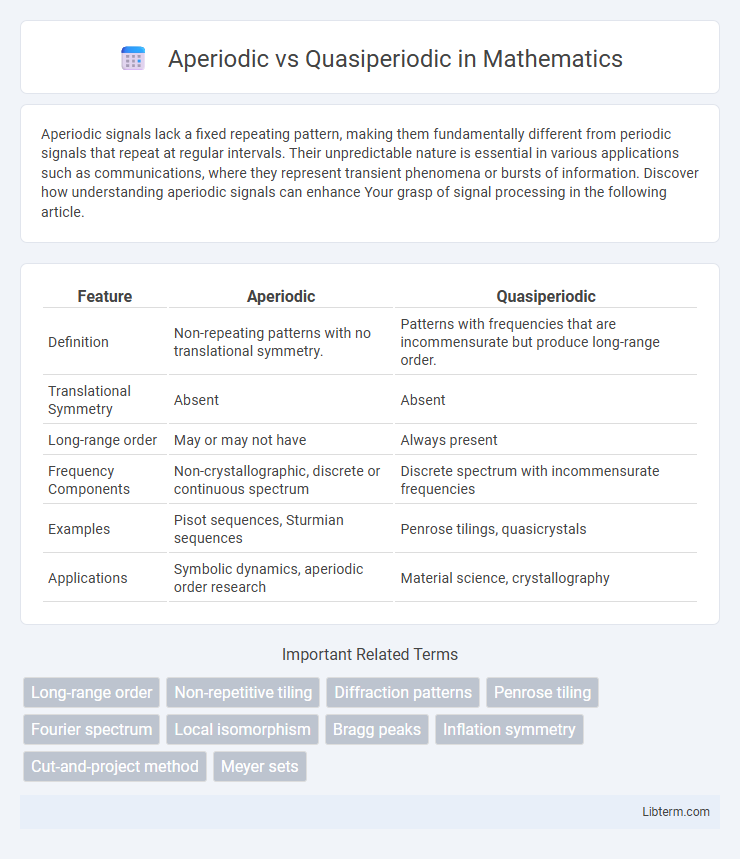
| Feature | Aperiodic | Quasiperiodic |
|---|---|---|
| Definition | Non-repeating patterns with no translational symmetry. | Patterns with frequencies that are incommensurate but produce long-range order. |
| Translational Symmetry | Absent | Absent |
| Long-range order | May or may not have | Always present |
| Frequency Components | Non-crystallographic, discrete or continuous spectrum | Discrete spectrum with incommensurate frequencies |
| Examples | Pisot sequences, Sturmian sequences | Penrose tilings, quasicrystals |
| Applications | Symbolic dynamics, aperiodic order research | Material science, crystallography |
Understanding Aperiodicity: Definition and Characteristics
Aperiodicity refers to patterns or signals that lack a regular, repeating interval over time or space, distinguishing them from periodic structures that exhibit exact repetition. Aperiodic sequences, such as those found in quasicrystals or certain mathematical models, display order without periodic repetition, often characterized by complex, non-repeating arrangements that defy classical symmetry. Understanding aperiodicity involves analyzing these unique structures through tools like Fourier transforms to identify their distinctive spectral properties, which reveal non-repeating but deterministic patterns fundamental to fields such as crystallography and signal processing.
What Does Quasiperiodic Mean? Key Insights
Quasiperiodic refers to patterns or signals that exhibit frequencies composed of two or more incommensurate base frequencies, creating a structure that never exactly repeats yet maintains an ordered form. Unlike aperiodic signals, which lack any regularity, quasiperiodic systems demonstrate predictability through a combination of periodic components without a common period. Key insights highlight quasiperiodicity in fields such as crystallography, where quasicrystals display non-repeating atomic arrangements that challenge traditional notions of symmetry.
Mathematical Foundations: Aperiodic vs. Quasiperiodic Structures
Aperiodic structures lack translational symmetry and do not repeat regularly, characterized by non-repeating sequences such as those generated by substitution rules in symbolic dynamics. Quasiperiodic structures exhibit long-range order with patterns formed by the superposition of periodic functions having incommensurate frequencies, described mathematically by quasiperiodic functions and studied through harmonic analysis on higher-dimensional tori. The mathematical foundations distinguish aperiodic tilings, like Penrose tilings, from quasiperiodic patterns by their non-crystallographic symmetries and unique spectral properties in spectral theory and ergodic theory.
Real-World Examples: Spotting Aperiodic Patterns
Aperiodic patterns, unlike quasiperiodic ones, lack regular intervals and are commonly observed in phenomena like heartbeat irregularities and stock market fluctuations. Real-world examples include seismic activity where earthquake occurrences cannot be precisely predicted due to their aperiodic nature. Quasiperiodic patterns, found in quasicrystals and certain astronomical orbits, display ordered but non-repeating structures that contrast sharply with the randomness of aperiodic sequences.
Quasiperiodicity in Nature and Technology
Quasiperiodicity in nature manifests through structures like quasicrystals, exhibiting ordered yet non-repeating atomic arrangements that challenge traditional crystallography. This unique arrangement results in distinctive physical properties such as unusual thermal conductivity and electronic behavior, useful in advanced materials science. In technology, quasiperiodic patterns influence photonic quasicrystals to control light propagation and optimize optical devices, enabling innovations in telecommunications and laser engineering.
How to Distinguish Aperiodic from Quasiperiodic Systems
Aperiodic systems lack any repeating pattern or long-range order, resulting in unpredictable and non-repetitive behavior over time, while quasiperiodic systems exhibit multiple incommensurate frequencies that create deterministic but non-repeating patterns. Distinguishing aperiodic from quasiperiodic systems involves analyzing their frequency spectrum: quasiperiodic systems show discrete peaks at irrational frequency ratios, whereas aperiodic systems display a continuous or broadband spectrum. Techniques such as Fourier analysis, Poincare sections, and Lyapunov exponent calculations help identify quasiperiodicity through the presence of stable, non-integer frequency combinations and distinguish it from chaotic or random aperiodic dynamics.
Applications of Aperiodic Structures in Science
Aperiodic structures, characterized by their non-repeating patterns, find critical applications in materials science, particularly in the development of quasicrystals used for creating durable, non-stick coatings and enhancing thermal insulation. These structures enable advances in photonics, where aperiodic photonic crystals manipulate light propagation for efficient optical filters and sensors. Research in nanotechnology leverages aperiodic arrangements to design catalysts with improved reactivity and selectivity due to their unique surface properties.
Uses of Quasiperiodic Patterns in Modern Research
Quasiperiodic patterns are extensively used in material science to design quasicrystals with unique electronic and thermal properties that defy traditional periodic lattices. In physics, these patterns model complex systems such as wave propagation and quantum mechanics, enabling advancements in photonic devices and metamaterials. Computational biology applies quasiperiodic sequences to analyze genetic codes and protein folding, enhancing the understanding of biological rhythms and structural formations.
Challenges in Studying Aperiodic and Quasiperiodic Phenomena
Studying aperiodic and quasiperiodic phenomena presents significant challenges due to their complex, non-repeating structures that defy traditional periodic analysis methods. The inherent unpredictability in aperiodic systems and the subtle order in quasiperiodic patterns require advanced mathematical tools like Fourier transforms and spectral analysis to identify underlying regularities. Furthermore, computational modeling and experimental validation are complicated by the sensitivity of these phenomena to initial conditions and external perturbations, making precise characterization and prediction difficult.
Future Prospects: Trends and Innovations in Pattern Analysis
Aperiodic and quasiperiodic pattern analysis is advancing rapidly with innovations in machine learning and computational geometry, enabling more precise detection in complex datasets such as quasicrystals and non-repetitive signal sequences. Emerging trends highlight increased integration of topological data analysis and spectral methods to distinguish subtle structural differences, enhancing applications in material science, cryptography, and bioinformatics. Future prospects suggest real-time monitoring and adaptive algorithms will drive breakthroughs in interpreting aperiodic and quasiperiodic patterns for predictive modeling and advanced diagnostic tools.
Aperiodic Infographic
 libterm.com
libterm.com