A vector bundle is a topological construction that associates a vector space to every point of a base space, allowing for the smooth variation of linear structures across the manifold. These bundles play a crucial role in fields like differential geometry, topology, and theoretical physics by providing a framework for analyzing local and global properties. Explore the rest of this article to deepen your understanding of how vector bundles impact various mathematical and physical theories.
Table of Comparison
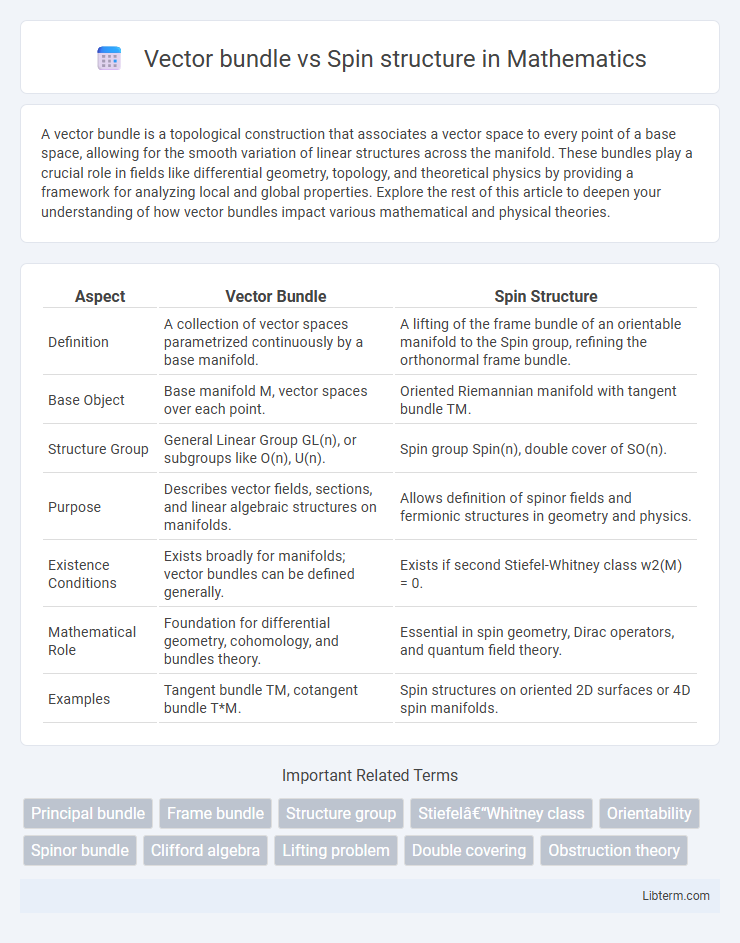
| Aspect | Vector Bundle | Spin Structure |
|---|---|---|
| Definition | A collection of vector spaces parametrized continuously by a base manifold. | A lifting of the frame bundle of an orientable manifold to the Spin group, refining the orthonormal frame bundle. |
| Base Object | Base manifold M, vector spaces over each point. | Oriented Riemannian manifold with tangent bundle TM. |
| Structure Group | General Linear Group GL(n), or subgroups like O(n), U(n). | Spin group Spin(n), double cover of SO(n). |
| Purpose | Describes vector fields, sections, and linear algebraic structures on manifolds. | Allows definition of spinor fields and fermionic structures in geometry and physics. |
| Existence Conditions | Exists broadly for manifolds; vector bundles can be defined generally. | Exists if second Stiefel-Whitney class w2(M) = 0. |
| Mathematical Role | Foundation for differential geometry, cohomology, and bundles theory. | Essential in spin geometry, Dirac operators, and quantum field theory. |
| Examples | Tangent bundle TM, cotangent bundle T*M. | Spin structures on oriented 2D surfaces or 4D spin manifolds. |
Introduction to Vector Bundles and Spin Structures
Vector bundles consist of a base manifold paired with a vector space smoothly attached to each point, serving as fundamental tools in differential geometry and topology. Spin structures refine the concept of orientable vector bundles by introducing a lift of the frame bundle to the Spin group, enabling the definition of spinor fields and the study of fermionic particles in mathematical physics. Understanding the relationship between vector bundles and Spin structures is crucial for exploring geometric and topological properties such as characteristic classes and Dirac operators on manifolds.
Fundamental Concepts: Vector Bundle Overview
A vector bundle is a topological construction where a vector space is parametrically attached to each point of a base manifold, allowing for the study of linear algebraic structures in a continuous setting. The fibers of a vector bundle vary smoothly over the base space, enabling local trivializations that resemble Cartesian products but with twisting in global topology. Understanding vector bundles is essential for grasping spin structures, as the latter refine vector bundles by incorporating additional geometric data to define spinor fields.
Understanding Spin Structures: A Brief Summary
Spin structures arise as refinements of vector bundles, specifically when lifting the principal SO(n)-bundle of an oriented Riemannian manifold to its double cover Spin(n). This lifting addresses issues related to the manifold's second Stiefel-Whitney class w_2, which obstructs the existence of spin structures; a spin structure exists if and only if w_2 vanishes. Understanding spin structures is essential in fields like differential geometry and theoretical physics, where they enable the definition of spinor fields and the formulation of fermionic quantum theories.
The Relationship Between Vector Bundles and Spin Structures
Vector bundles serve as the fundamental geometric objects whose tangent bundle structure can admit spin structures, providing a lift of the principal SO(n)-bundle to a principal Spin(n)-bundle. Spin structures exist only when the second Stiefel-Whitney class of the vector bundle vanishes, reflecting a topological obstruction and linking the vector bundle's characteristic classes to the existence of spinors. This relationship underpins the study of spin geometry, where the interplay between vector bundles and spin structures facilitates the analysis of manifolds with additional spinorial data crucial in both mathematics and theoretical physics.
Topological Obstructions: When Does a Spin Structure Exist?
A vector bundle admits a spin structure if and only if its second Stiefel-Whitney class vanishes, specifically \( w_2 = 0 \) in cohomology. This topological obstruction arises because lifting the structure group from SO(n) to Spin(n) requires nullifying \( w_2 \), which measures the failure to define consistent spinor fields. Therefore, the existence of a spin structure is equivalent to the triviality of this obstruction, ensuring the bundle's orientability and the ability to define spinor bundles.
Characteristic Classes and Their Role in Spin Geometry
Characteristic classes such as Stiefel-Whitney and Chern classes provide key invariants for vector bundles, detecting obstructions to the existence of spin structures on manifolds. In particular, the second Stiefel-Whitney class \( w_2 \) plays a crucial role, with its vanishing being a necessary and sufficient condition for a spin structure to exist. Spin geometry leverages these classes to analyze the topological constraints of spin bundles, enabling deep insights into metric and Dirac operator properties on smooth manifolds.
Construction of Spin Structures on Vector Bundles
Spin structures on vector bundles arise from lifting the principal SO(n)-bundle of oriented orthonormal frames to a principal Spin(n)-bundle, reflecting the double cover Spin(n) - SO(n). Constructing a Spin structure involves verifying the vanishing of the second Stiefel-Whitney class w2 of the vector bundle, as this obstruction class determines the existence of such a lift. Explicitly, given an oriented vector bundle with structure group SO(n), a Spin structure corresponds to a principal Spin(n)-bundle together with a 2-to-1 bundle map covering the identity on the base manifold and intertwining the group actions via the covering homomorphism.
Applications in Geometry and Theoretical Physics
Vector bundles provide the mathematical framework for describing fields and gauge theories in geometry and theoretical physics, serving as the basis for fiber bundles associated with tangent spaces on manifolds. Spin structures refine vector bundles by enabling the definition of spinor fields, crucial for formulating fermions in quantum field theory and studying index theorems on spin manifolds. Applications include the classification of anomalies in gauge theories, the study of Dirac operators in geometry, and the formulation of supersymmetric models where spin structures are essential to define spinor fields consistently.
Examples and Case Studies: Comparing Vector Bundles and Spin Structures
Vector bundles like the tangent bundle on a sphere illustrate geometric structures underpinning manifold theory, while spin structures arise in cases such as spin manifolds important in theoretical physics and differential geometry. For example, the tangent bundle on a 2-dimensional sphere \(S^2\) lacks a spin structure due to its nontrivial second Stiefel-Whitney class, contrasting with the 3-dimensional sphere \(S^3\), which admits a spin structure because it is simply connected and spin cobordant to a point. Case studies in index theory reveal how spin structures enable defining Dirac operators on vector bundles, crucial in understanding fermionic fields and topological invariants in mathematical physics.
Conclusion: Key Differences and Interconnections
Vector bundles serve as general frameworks for associating vector spaces to manifolds, while Spin structures provide specific refinements that enable defining spinor fields and addressing topological obstructions in orientable manifolds. The key difference lies in Spin structures requiring the lifting of the frame bundle's structure group from SO(n) to its double cover Spin(n), which is not guaranteed for all vector bundles. Interconnections emerge in geometry and physics where Spin structures refine vector bundles, crucial for studying Dirac operators and quantum field theory on manifolds with spin topology.
Vector bundle Infographic
 libterm.com
libterm.com