The quadratic mean, also known as the root mean square (RMS), is a statistical measure used to determine the average magnitude of a set of numbers, especially useful when values can be both positive and negative. It is calculated by taking the square root of the average of the squares of the numbers, providing a more accurate representation of magnitude in contexts like signal processing and physics. Explore the rest of the article to understand how the quadratic mean applies to your data analysis.
Table of Comparison
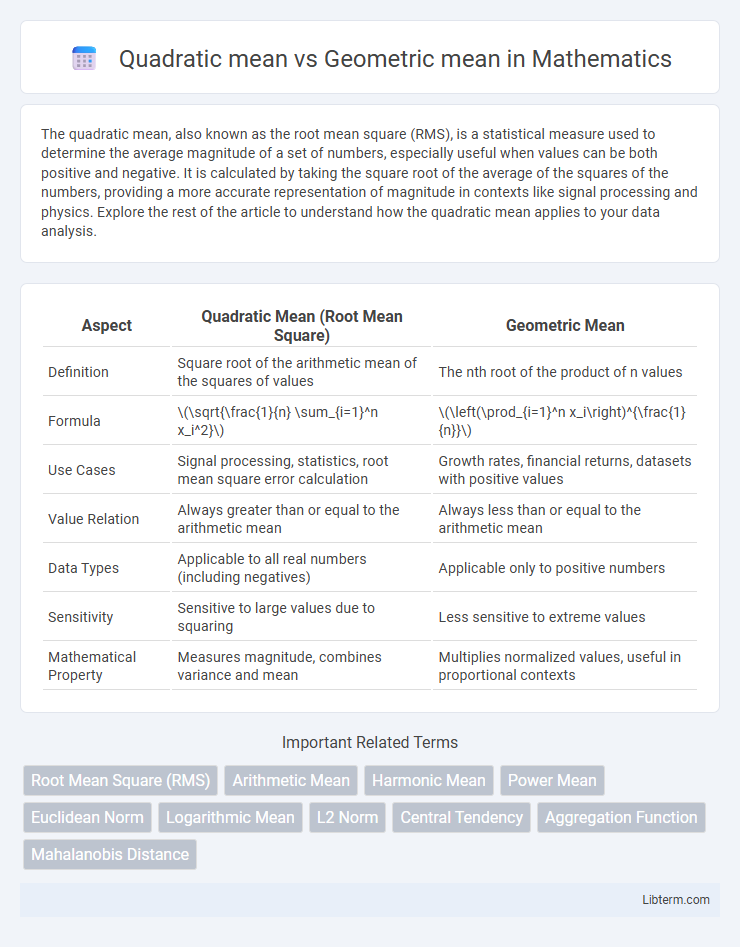
| Aspect | Quadratic Mean (Root Mean Square) | Geometric Mean |
|---|---|---|
| Definition | Square root of the arithmetic mean of the squares of values | The nth root of the product of n values |
| Formula | \(\sqrt{\frac{1}{n} \sum_{i=1}^n x_i^2}\) | \(\left(\prod_{i=1}^n x_i\right)^{\frac{1}{n}}\) |
| Use Cases | Signal processing, statistics, root mean square error calculation | Growth rates, financial returns, datasets with positive values |
| Value Relation | Always greater than or equal to the arithmetic mean | Always less than or equal to the arithmetic mean |
| Data Types | Applicable to all real numbers (including negatives) | Applicable only to positive numbers |
| Sensitivity | Sensitive to large values due to squaring | Less sensitive to extreme values |
| Mathematical Property | Measures magnitude, combines variance and mean | Multiplies normalized values, useful in proportional contexts |
Introduction to Means: Quadratic vs Geometric
Quadratic mean, also known as root mean square (RMS), is calculated by taking the square root of the average of the squares of a set of values, making it especially useful in contexts involving varying magnitudes such as physics and engineering. Geometric mean is the nth root of the product of n values, emphasizing proportional growth and often applied in finance, population studies, and multiplicative processes. Both means provide unique insights into data sets, with quadratic mean highlighting magnitude differences and geometric mean focusing on relative change and multiplicative relationships.
Definition of Quadratic Mean
The quadratic mean, also known as the root mean square (RMS), is defined as the square root of the arithmetic mean of the squares of a set of values. This measure captures the magnitude of numbers, emphasizing larger values due to the squaring process. In contrast, the geometric mean calculates the nth root of the product of n values, representing the central tendency in multiplicative contexts.
Definition of Geometric Mean
The geometric mean is defined as the nth root of the product of n positive numbers, serving as a measure of central tendency that emphasizes multiplicative relationships and proportional growth. Unlike the quadratic mean, which calculates the square root of the average of squares and is sensitive to larger values, the geometric mean provides a more appropriate average for datasets involving rates of change, ratios, or percentages. This makes the geometric mean particularly useful in fields such as finance, biology, and environmental science where compound growth and relative changes are essential.
Mathematical Formulas and Notations
The quadratic mean, represented as \( Q = \sqrt{\frac{1}{n} \sum_{i=1}^n x_i^2} \), calculates the square root of the average of the squares of a set of values \( x_i \). The geometric mean, denoted by \( G = \left( \prod_{i=1}^n x_i \right)^{\frac{1}{n}} \), computes the nth root of the product of the values. Both means are used in different contexts: the quadratic mean emphasizes larger values due to squaring, while the geometric mean is suitable for datasets involving multiplicative relationships.
Key Differences Between Quadratic and Geometric Means
The quadratic mean, also known as the root mean square (RMS), calculates the square root of the average of the squares of a set of values, emphasizing larger magnitudes, while the geometric mean multiplies all values and takes the nth root, focusing on proportional growth or rates of change. Quadratic mean is particularly useful in contexts involving power or energy, such as signal processing, whereas the geometric mean is preferred for datasets with positive numbers involving ratios or percentages, like financial returns. The quadratic mean is always greater than or equal to the geometric mean due to the Cauchy-Schwarz inequality, reflecting their different sensitivities to data variation.
Applications of Quadratic Mean
The quadratic mean, also known as the root mean square (RMS), is widely applied in physics and engineering to calculate varying quantities such as electrical current, sound intensity, and signal processing because it effectively measures the magnitude of oscillations or fluctuations. It is particularly useful in contexts where both positive and negative values exist, as it ensures a non-negative average that reflects the power or energy of a dataset, unlike the geometric mean which is better suited for multiplicative processes and growth rates. The quadratic mean's ability to emphasize larger values makes it crucial for analyzing datasets related to wave amplitudes, vibration analysis, and error measurement in statistics.
Common Uses of Geometric Mean
The geometric mean is widely used in finance to calculate average rates of return over multiple periods, providing a more accurate measure than the arithmetic or quadratic mean when dealing with compounded growth. It is essential in fields like biology and environmental science for analyzing proportional growth rates or concentration levels, where data are multiplicative rather than additive. Unlike the quadratic mean, which emphasizes larger values and is common in physics and engineering for root mean square calculations, the geometric mean effectively handles datasets with varying scales and exponential changes.
Strengths and Limitations of Each Mean
The quadratic mean, also known as the root mean square, excels in emphasizing larger values, making it ideal for datasets involving power or intensity measurements, but it can be overly influenced by outliers. The geometric mean is best suited for datasets with multiplicative or proportional relationships, providing a more balanced average when dealing with growth rates or ratios, but it cannot handle zero or negative values. While the quadratic mean captures variance effectively, the geometric mean offers stability with skewed data but less sensitivity to extreme deviations.
Practical Examples and Calculations
Quadratic mean, also known as root mean square, is used extensively in electrical engineering to calculate effective voltage or current, with the formula ((x12 + x22 + ... + xn2)/n). Geometric mean is applied in finance to determine average growth rates, especially for investment returns, computed as the nth root of the product of n values (x1 * x2 * ... * xn)^(1/n). For example, given values 2, 4, and 8, the quadratic mean is ((22 + 42 + 82)/3) 5.94, while the geometric mean is (2 * 4 * 8)^(1/3) 4.0, illustrating how quadratic mean emphasizes larger values more.
Choosing the Right Mean: Guidelines and Tips
Choosing between the quadratic mean and geometric mean depends on the data's nature and the analysis goal. Use the quadratic mean for datasets emphasizing larger values, common in engineering and signal processing, as it gives more weight to higher magnitudes. Opt for the geometric mean in multiplicative contexts or growth rates, such as finance or biology, where product relationships and proportional change are critical for accurate averaging.
Quadratic mean Infographic
 libterm.com
libterm.com