Haar measure provides a way to assign an invariant volume to subsets of locally compact topological groups, ensuring consistency under group translations. This concept is fundamental in harmonic analysis, probability theory, and representation theory, allowing integration over complex group structures. Explore the article to understand how Haar measure can be applied to your mathematical problems and research.
Table of Comparison
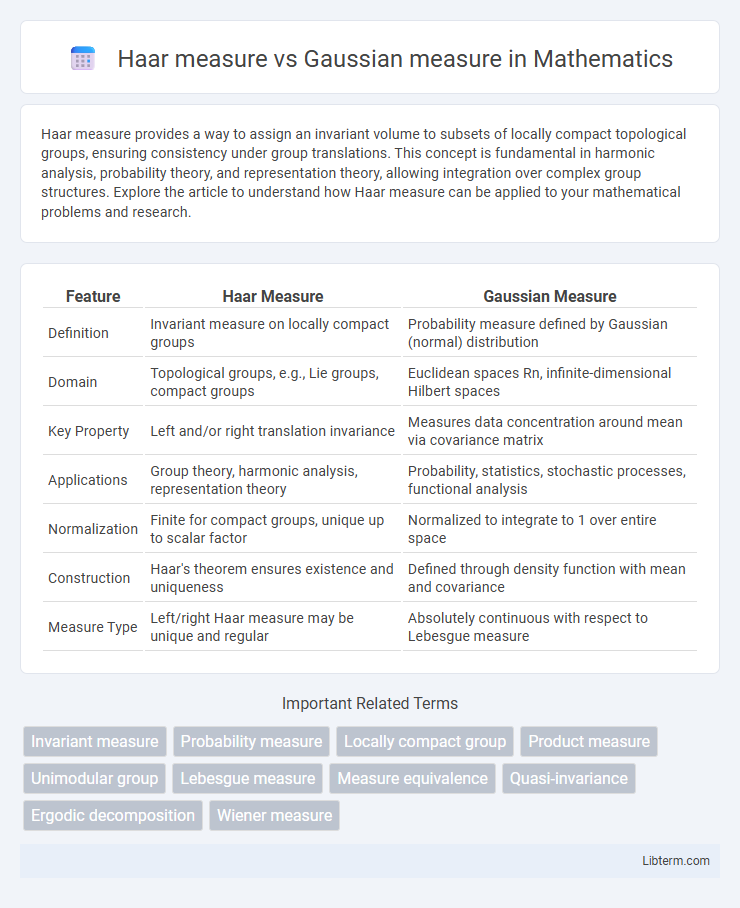
| Feature | Haar Measure | Gaussian Measure |
|---|---|---|
| Definition | Invariant measure on locally compact groups | Probability measure defined by Gaussian (normal) distribution |
| Domain | Topological groups, e.g., Lie groups, compact groups | Euclidean spaces Rn, infinite-dimensional Hilbert spaces |
| Key Property | Left and/or right translation invariance | Measures data concentration around mean via covariance matrix |
| Applications | Group theory, harmonic analysis, representation theory | Probability, statistics, stochastic processes, functional analysis |
| Normalization | Finite for compact groups, unique up to scalar factor | Normalized to integrate to 1 over entire space |
| Construction | Haar's theorem ensures existence and uniqueness | Defined through density function with mean and covariance |
| Measure Type | Left/right Haar measure may be unique and regular | Absolutely continuous with respect to Lebesgue measure |
Introduction to Haar and Gaussian Measures
Haar measure is a unique translation-invariant measure defined on locally compact topological groups, fundamental in harmonic analysis and representation theory. Gaussian measure, concentrated on infinite-dimensional spaces like Hilbert spaces, generalizes the normal distribution to functional analysis and probability theory. Both measures serve as essential tools in studying group symmetries and stochastic processes, with Haar measure ensuring uniform integration on groups and Gaussian measure characterizing distributions in infinite dimensions.
Fundamental Concepts: Measure Theory Overview
Haar measure is a unique translation-invariant measure defined on locally compact topological groups, providing a foundation for integration and symmetry analysis in abstract algebraic structures. Gaussian measure, in contrast, is a probability measure on infinite-dimensional spaces such as Hilbert or Banach spaces, characterized by its mean vector and covariance operator, fundamental in stochastic processes and functional analysis. Both measures rely on measure theory concepts like sigma-algebras and measurable functions but serve distinct roles: Haar measure emphasizes invariant integration over groups, whereas Gaussian measure focuses on probabilistic distributions in infinite dimensions.
Defining the Haar Measure
The Haar measure is a unique translation-invariant measure defined on locally compact topological groups, enabling integration over these groups in a way that respects the group structure. In contrast to the Gaussian measure, which is defined on Euclidean spaces with density related to the normal distribution, the Haar measure generalizes the concept of uniform measure to non-abelian groups and is critical for harmonic analysis and representation theory. Its invariance property ensures that the measure of any measurable set remains consistent under group multiplication, making it fundamental in abstract harmonic analysis.
Gaussian Measure: Key Properties
Gaussian measure on infinite-dimensional spaces is characterized by its mean vector and covariance operator, enabling the study of probability distributions in functional analysis and stochastic processes. It is translation-invariant with respect to shifts in Hilbert or Banach spaces, preserving measure under linear transformations that maintain covariance structure. The measure exhibits properties such as tightness, regularity, and the concentration of measure phenomenon, making it fundamental in fields like statistical mechanics and quantum field theory.
Invariance: Haar vs. Gaussian
Haar measure is defined on locally compact groups and is invariant under group translations, meaning it remains unchanged when the group elements are shifted, ensuring uniformity across the group structure. In contrast, Gaussian measure, typically defined on infinite-dimensional Hilbert spaces or Euclidean spaces, is not translation-invariant but instead enjoys invariance under orthogonal transformations preserving the Gaussian distribution's covariance structure. This fundamental difference highlights Haar measure's role in harmonic analysis on groups, while Gaussian measure is central to probability theory and functional analysis due to its rotational invariance and specific covariance properties.
Applications in Probability and Analysis
Haar measure provides a translation-invariant measure on locally compact groups, essential for studying symmetries and group actions in probability theory and harmonic analysis. Gaussian measure, defined on infinite-dimensional spaces or Euclidean spaces, is pivotal in probability for modeling distributions of random variables and functions, particularly in stochastic processes and functional analysis. Both measures facilitate rigorous integration frameworks, with Haar measure underpinning invariant integration on groups and Gaussian measure enabling analysis of normal distributions and their generalizations.
Role in Topological Groups
Haar measure serves as a unique translation-invariant measure on locally compact topological groups, enabling integration and harmonic analysis by assigning consistent volume across group elements. Gaussian measure, defined on infinite-dimensional vector spaces, lacks translation invariance but is crucial for studying probability distributions in topological vector spaces and functional analysis. The Haar measure's invariance under group operations contrasts with the Gaussian measure's focus on probabilistic structure, making each fundamental in different aspects of topological group theory and measure theory.
Measure Uniqueness and Normalization
Haar measure on a locally compact group is unique up to a positive scalar multiple and can be normalized so that the total measure of the compact group is one, ensuring invariance under group translation. Gaussian measure, defined on Euclidean spaces, is uniquely determined by its mean and covariance matrix, with normalization fixed by integrating to one over the entire space according to the Gaussian integral formula. Uniqueness in Haar measure hinges on translation invariance, while Gaussian measure's uniqueness and normalization arise from its probability density function properties.
Connections to Representation Theory
Haar measure on locally compact groups provides an invariant integration tool critical for analyzing group representations, enabling decomposition into irreducible components in representation theory. Gaussian measure, with its central role in infinite-dimensional Hilbert spaces, connects to representation theory through the study of Gaussian unitary ensembles and canonical commutation relations in quantum mechanics. Both measures facilitate constructing unitary representations, with Haar measure yielding uniform averaging over groups and Gaussian measure underpinning probabilistic and functional analytic methods in representation theory.
Summary: Comparing Use Cases and Limitations
Haar measure provides a unique, translation-invariant measure on locally compact groups, making it ideal for analyzing symmetries and group actions in harmonic analysis and representation theory. Gaussian measure, centered on infinite-dimensional vector spaces with properties tied to the normal distribution, excels in probability theory, stochastic processes, and functional analysis involving random fields. Limitations of Haar measure include applicability only to groups with suitable topology, while Gaussian measure's constraints lie in its reliance on measure concentration and infinite-dimensional Hilbert space structures for theoretical guarantees.
Haar measure Infographic
 libterm.com
libterm.com